Міні-підручник "Задачі на множення і ділення дробів"

Про матеріал

Тренувально-узагальнюючий збірник завдань з математики "Задачі на множення і ділення дробів" для учнів 6 класу

Перегляд файлу

$C:\Users\Саня\Desktop\Картинки для гімназії\ФОН для уроков\0_8504d_e97480e2_XL.jpg$

Тренувально-узагальнюючий збірник завдань розроблено на кафедрі природничо-математичних дисциплін.

Автор-укладач Бережна Юлія Миколаївна – вчитель математики.

$C:\Users\Саня\Desktop\boybook1.gif$

Емблема гимназии

Гімназія № 107 «Введенська»

Кафедра математики

Тренувально-узагальнюючий

збірник завдань

з математики

учня (учениці) 6 – __ класу

_________________________________

⁽^{Прізвище, ім’я учня (учениці))}

Київ – 2020

$C:\Users\Саня\Desktop\aufgabenliste_add1.jpg$ Розв'язування задач є найхарактернішим і специфічним різновидом вільного мислення.

В. Джеймс

$C:\Users\Саня\Desktop\owl-key-logo.gif$

Математична гра «Намалюй сонечко»

$C:\Users\Саня\Desktop\Картинки для гімназії\Новая папка (3)\kisto4karisovanie.gif$ $C:\Users\Саня\Desktop\Безымянный.jpg$

1. ЯК ЗНАЙТИ ДРІБ ВІД ЧИСЛА?

Задача 1.1

У класі навчається 30 учнів, з них – дівчата. Скільки дівчат у класі?

5 клас

6 клас

1) (учнів) – становить від 30 учнів;

2) (учнів) – становить від 30 учнів.

Отже, у класі 18 дівчат.

(учнів) – становить від 30 учнів.

Отже, у класі 18 дівчат.

$C:\Users\Саня\Desktop\11.png$

Щоб знайти дріб від числа, потрібно число помножити на цей дріб.

Задача 1.2

У школі навчається 425 учнів, 56% з них дівчата. Скільки дівчат у школі?

Запишемо 56% у вигляді дробу: 56%=0,56. Щоб дати відповідь на запитання задачі, потрібно знайти 56% від 425 ,або дріб 0,56 від 425.

(дівчаток) – навчається у школі.

$C:\Users\Саня\Desktop\11.png$ Щоб знайти відсотки від числа, потрібно записати відсотки у вигляді дробу і помножити число на цей дріб.

Виконай завдання:

1. $C:\Users\Саня\Desktop\Міні-підручник ЗАДАЧІ НА МНОЖЕННЯ І ДІЛЕННЯ ДРОБІВ\image.gif$ Знайди від 120 .

_________________________________________________

____________________________________________________________

2. У саду 40 дерев. Серед них є яблуні та груші. Скільки в саду яблунь, якщо: а) яблунь усіх дерев; б) груш усіх дерев.

$C:\Users\Саня\Desktop\Картинки для гімназії\Новая папка (3)\1302175305_grusha_sliva - копия.jpg$ ____________________________________________

____________________________________________

_____________________________________

3. Висота гори Граб в Карпатах дорівнює близько 1300 м, гора Сивуля приблизно в разу вища від Грабу, а гора Говерла в разу вища від Сивулі. Знайти висоти цих гір.

__________________________________________

______________________________________________________________

4. У жовтні пакет акцій фірми коштував 2000 грн., у грудні його вартість зросла на 5%. Якою стала вартість пакета акцій у грудні?

_____________________________________

______________________________________________________________

$C:\Users\Саня\Desktop\Картинки для гімназії\000d69e7 - копия.jpeg$ 5. Велосипедист за першу годину подолав 40% дистанції, а за другу – 70% решти дистанції. Скільки відсотків дистанції проїхав велосипедист за ці дві години?

_____________________________________________________

______________________________________________________________

2. ЯК ЗНАЙТИ ЧИСЛО ЗА ЙОГО ДРОБОМ?

Задача 2.1

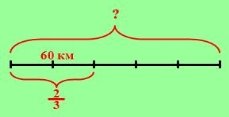
Автомобіль, рухаючись від міста А до міста В, проїхав 60 км, що становить відстані між цими містами. Яка відстань між цими містами?

5 клас

6 клас

1) (км) – придає на відстані;

2) (км) – відстань

між містами.

Отже, відстань між містами становить 150 км.

(км) – відстань

між містами.

Отже, відстань між містами становить 150 км.

У задачі відомо, що відстані – це 60 км, а потрібно знайти всю відстань, тобто в задачі відомо, чому дорівнює дріб від числа, а потрібно знайти саме число.

$C:\Users\Саня\Desktop\1212.jpg$

знайшли число за значенням його дробу

$C:\Users\Саня\Desktop\11.png$

Щоб знайти число за даним значенням його дробу, потрібно це значення поділити на дріб.

Задача 2.2

З чайного листа виходить 4,5% чаю. Скільки потрібно взяти чайного листа, щоб отримати 36 кг чаю?

Запишемо 4,5% у вигляді дробу: 4,5%=4,5:100=0,045. Потрібно знайти масу чайного листа, якщо 0,045 цієї маси становить 36 кг, тобто потрібно знайти число за даним значенням його дробу: (кг)

Отже, щоб отримати 36 кг чаю, потрібно взяти 800 кг чайного листа.

$C:\Users\Саня\Desktop\2121.jpg$

знайшли число за значенням його відсотків

$C:\Users\Саня\Desktop\11.png$

Щоб знайти число за його відсотками, потрібно записати відсотки дробом і поділити значення відсотків на одержаний дріб.

$C:\Users\Саня\Desktop\Міні-підручник ЗАДАЧІ НА МНОЖЕННЯ І ДІЛЕННЯ ДРОБІВ\image.gif$ Виконай завдання:

1. Знайди число, якого дорівнює 45.

_________________________________________________

2. Знайди число, якого дорівнює 14.

____________________________________________________________

3. Кукурудзою засіяли 78 га поля, що становить площі всього поля. Яка площа всього поля? Нарисуйте схему для розв’язання задачі.

____________________________________________

Схема

4. Перша сторона трикутника дорівнює м, друга і третя – відповідно в й разу коротші від першої. Знайдіть периметр трикутника.

_______________________________________________

______________________________________________________________

5. Після того як туристи пройшли запланованого шляху, їм залишилося пройти ще км. Знайдіть запланований шлях. Скористайся схемою:

Схема

$C:\Users\Саня\Desktop\3132.jpg$

______________________________________________________________

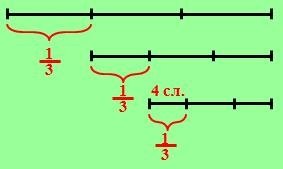
6. Мама залишила для трьох синів тарілку слив, а сама пішла на роботу. Першим зі школи прийшов молодший син, він побачив на тарілці сливи, з’їв третю частину і пішов гуляти. Другим прийшов середній син. Подумавши, що його брати ще не ласували сливами, він з’їв третю частину тих, що були на тарілці, й теж пішов гуляти. Останнім прийшов старший син і з’їв 4 сливи – третю частину тих, що були на тарілці. Скільки слив було на тарілці спочатку?

Скористайся схемою:

$C:\Users\Саня\Desktop\вім2ц.jpg$

______________________________________________________________

Дещо з історії

Дії над дробами, і особливо дію ділення, колись вважали надзвичайно важкими. Правило ділення на дріб почали застосовувати спочатку китайські, а пізніше й індійські математики VІІ-ІХ ст. Щоб поділити дроби, спочатку зводили їх до спільного знаменника, після чого чисельник діленого ділити на чисельник дільника. У 1544 р. німецький математик М. Штіфель сформулював правило ділення на дріб як множення на обернений дріб.

Міхаель Штіфель

Задачі на множення і ділення дробів

В даному тренувально-узагальнюючому збірнику подані завдання з двох тем. В першій темі «Задачі на множення дробів» насамперед потрібно приділити увагу наочній демонстрації дітям поняття «знаходження дробу від числа» та його практичного використання. Цьому сприяє велика кількість текстових задач. Слід звернути увагу дітей на те, що поняття «знаходження дробу від числа» є однаковим і для звичайних дробів, і для десяткових, і для мішаних чисел, незважаючи на певні відмінності в алгоритмах виконання множення. Також діти мають засвоїти, що при роботі з відсотками слід перевести вказану кількість відсотків у дріб, поділивши її на 100 (головним джерелом помилок є те, що діти забувають це робити і отримують результат у 100 разів більший!).

В другій темі «Задачі на ділення дробів» потрібно приділити особливу увагу алгоритму знаходження числа за його дробом. Діти мають чітко усвідомити, у яких випадках застосовується алгоритм знаходження дробу від числа, а в яких – знаходження числа за його дробом. Слід також розглянути знаходження числа за його відсотками як окремий випадок знаходження числа за його дробом. Діти мають засвоїти, що як і для знаходження дробу від числа, відсотки потрібно представити у вигляді дробу.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Бережна Юлія Миколаївна

Пов’язані теми

Математика, 6 клас, Матеріали для друку

Додано

10 січня 2020

Переглядів

3032

Оцінка розробки

Відгуки відсутні