Найпростіші перетворення графіків функцій
Тема уроку: Найпростіші перетворення графіків функцій.
Мета уроку: Сформувати розуміння учнями змісту поняття «перетворення графіка функції», знання учнів про основні види геометричних перетворень графіків функцій, уміння «читати» графіки функцій (тобто за готовими графіками задавати рівняння функцій), сформувати навики виконувати побудови графіків функцій за допомогою перетворень, заданих рівнянням даної функції. Закріпити знання учнів про види геометричних перетворень графіків функцій і зв'язок між видом перетворення та видом рівняння, що задає дану функції, схеми міркувань, що передують побудові графіка деякої функції шляхом геометричних перетворень графіка однієї з елементарних функцій, вміння виконувати послідовні перетворення графіків елементарних функцій для побудови даних алгебраїчних функцій відповідно до складеної схеми дій.
Розвивати графічну культуру, здатність до передбачення результатів побудови.
Виховувати наполегливість, старанність.
Тип уроку: формування знань умінь і навиків.
Наочність та обладнання: Комп’ютери, ноутбук, програми Advanced Grapfer, MyTest,
Хід уроку
І. Перші 30 хвилин. Робота в кабінеті ІОТ.
- Актуалізація опорних знань.
а) повторити зображення графіків елементарних функцій;
б) організація поточного контролю за засвоєнням учнями знань та вмінь: виконання тестових завдань (див. нижче), перевірка яких проводиться одразу після завершення. Один учень біля дошки, решта учнів класу на картках з тестовим завданням
Фіксую прізвища тих учнів, які потребують додаткової уваги для можливості здійснення певної корекційної роботи.
Тестові завдання:
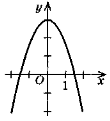
- На рисунку зображений графік функції, область визначення якої D(f) = R. Правильним є твердження:
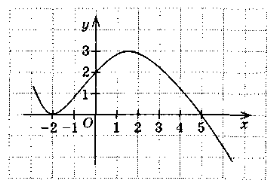
а) нулі функції: 2; 2,5; f(x) зростає, якщо х ![]() [-2; 3]; f(x) < 0, якщо x
[-2; 3]; f(x) < 0, якщо x ![]() (5; +∞);
(5; +∞);
б) нулі функції: 2; 5; f(x) зростає, якщо x ![]() [-2; 2]; f(x) < 0, якщо х
[-2; 2]; f(x) < 0, якщо х ![]() [5; +∞);
[5; +∞);
в) нулі функції:-2; 5; проміжок зростання x ![]() [-2; 2]; f(х) < 0, якщо х
[-2; 2]; f(х) < 0, якщо х ![]() (5; +∞);
(5; +∞);
г) нулі функції: 3; проміжку зростання немає; f(x) < 0, якщо x ![]() (-∞; -2) і x
(-∞; -2) і x ![]() (2; +∞).
(2; +∞).
-
Область визначення функції у =
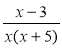 :
:
а) х ![]() 5; б) х
5; б) х ![]() -5; в) х
-5; в) х ![]() -5, х
-5, х ![]() 0; г) х
0; г) х ![]() 3.
3.
- Область значень функції f(x) = x2 – 3:
а) (-∞; +∞); б) [3; +∞); в) [-3; +∞); г) (-3; +∞).
-
Якщо f(x) = 3
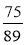 х – 1, то:
х – 1, то:
а) f (3) < f (4); б) f (3) > f (4); в) f (3) < f (4); г) f (3) = f (4).
- Значення функції у(х) = -3х + 8 додатні, якщо:
а) х ≤ 2![]() ; б) х ≥ 2
; б) х ≥ 2![]() ; в) х < 2
; в) х < 2![]() ; г) таких значень х немає.
; г) таких значень х немає.
6. Яка з наведених функцій є зростаючою:
а) на області визначення; б) на проміжках (-∞; 0) і (0; +∞)?
1) у = 4х – 1; 2) у = ![]() ; 3) у = -
; 3) у = -![]() x + 1; 4) у = 3х;
x + 1; 4) у = 3х;
5) у = ![]() ; 6) у = х2; 7) у = -
; 6) у = х2; 7) у = -![]() .
.
7. Графіком якої з наведених функцій є пряма, що проходить через початок координат? Поясніть свою відповідь, не виконуючи побудови:
1) у = 2х + 1; 2) у = 2х; 3) у = 2х2; 4) у = 2; 5) у = ![]() ; 6) у =
; 6) у = ![]() .
.
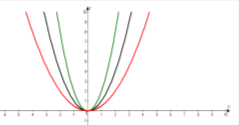
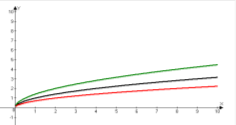
- На одному з рисунків зображено графік функції у = 2х. Укажіть цей рисунок.
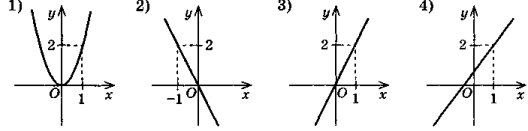
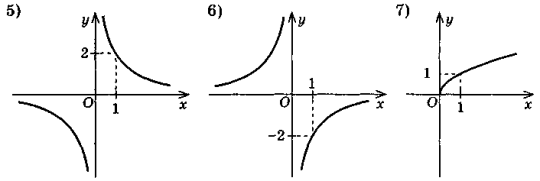
- Мотивація навчальної діяльності учнів
Ми з вами вже знаємо властивості елементарних функцій і ви вмієте будувати їх графіки. Виконана тестова робота показала, що описати властивості функції легше за графіком. Дослідження функцій за готовим графіком є більш простим, ніж за формулою (підтвердженням цієї думки можуть стати результати перевірки тестових завдань), в ряді випадків для розв'язування задач необхідно буває побудувати графік функції, яка не є елементарною. А чи існують засоби (і якщо існують, то як ними користуватися), за допомогою яких можна побудувати графік деякої функції, використовуючи при цьому вміння будувати графіки елементарних функцій (лінійної, оберненої пропорційності, квадратичної функції та функції у = ![]() )? Пошук відповіді на поставлене питання і є основною метою уроку.
)? Пошук відповіді на поставлене питання і є основною метою уроку.
- Повідомлення теми, мети уроку.
Для попереднього сприйняття даних знань використаємо комп’ютерну техніку
а) повторення навичок роботи з програмою Advanced Grapfer
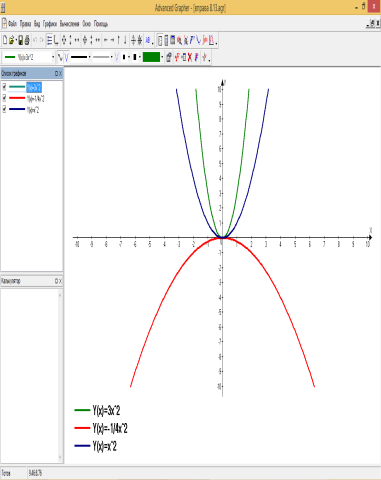
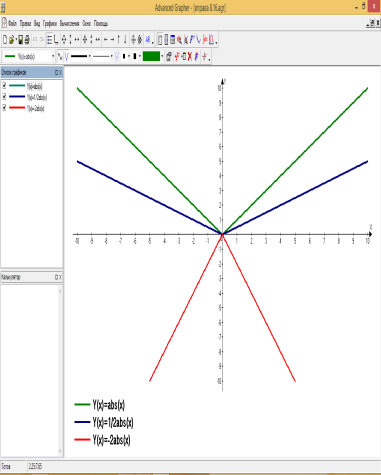
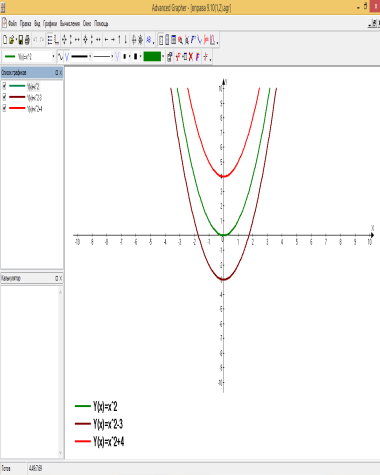
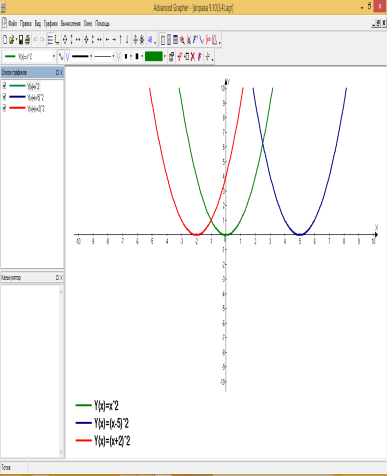
б) побудувати графіки функцій використовуючи програму Advanced Grapfer: Рис.8.2; 8.3 (на одному аркуші); 8.6; 8.10; 8.11; 8.12; 9.1; 9.2;9.5; 9.6
вправи: 8.13; 8.14; 8.16; 9.10; 9.12, 9.14,9.23; 9.25; 9.28.

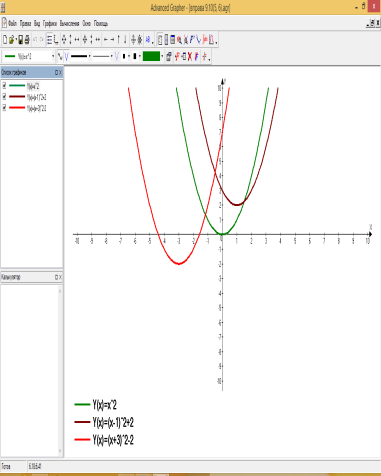
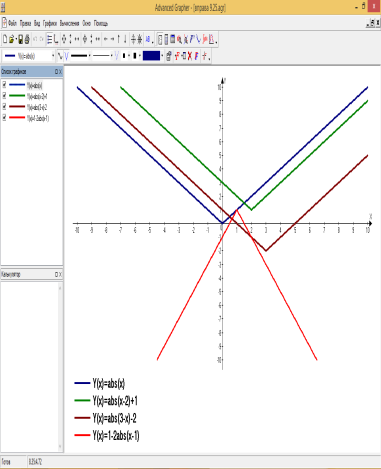

4. Підсумок перших 30-ти хвилин:
|
|
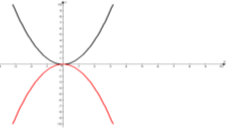
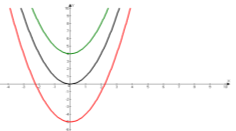
Графік якої функції зображений на рисунку? 1) у = х2 + 3; 2) у = х2 – 3; 3) у = -х2 + 3; 4) у = -х2 – 3. |
ІІ. Другі 30 хвилин. Робота в кабінеті математики.
1. Формування знань, умінь і навичок.
а) Виконання усних вправ:
Як треба перетворити графік функції y = f(x), щоб утворився графік функції:
1) y = -f(x); 2) y = f(x + 2); 3) y = f(x – 2); 4) y = f(x) + 2;
5) y = f(x) – 2; 6) y = 2f(x); 7) y = ![]() ?
?
б) Створення опорного конспекту:
Формування умінь виконувати перетворення графіків функцій:
а) аналіз формули даної функції;
б) вибір геометричного перетворення;
в) безпосереднє виконання перетворення графіка функції;
г) робота за підручником п.8, 9 ст 70-77, 81-86.Скласти опорний конспект:
- Які є види перетворень
- побудова y = kf(x)
- побудова y = -f(х))
- побудова y = f(kx)
- побудова y = f(-х)
- побудова y = f(х) + b
- побудова y = f(x+а)
|
|
Найпростіші перетворення графіків функцій |
|
|||
|
|
№ з/п |
Формула залежності |
Приклад |
Перетворення |
|
|
|
1 |
y = kf(x) k>0 |
|
Розтяг у k разів від осі абсцис, якщо k >1, або стиск у |
|
|
|
2 |
y = -f(х) |
|
Симетрія відносно осі абсцис |
|
|
|
3 |
y = f(kx) k>0 |
|
Стиск в k разів до осі ординат, якщо k >1, або в результаті розтяг в |
|
|
|
4 |
y = f(-х) |
|
Симетрія відносно осі ординат |
|
|
|
5 |
y = f(х) + b |
|
Паралельне перенесення вздовж осі Оу на b одиниць (якщо b > 0, то вгору, якщо b < 0, то вниз) |
|
|
|
6 |
y = f(х + a) |
|
Паралельне перенесення вздовж осі Ох на а одиниць вліво, якщо а > 0, і на -а одиниць вправо, якщо а < 0 |
|
|
|
|
|
|
|
|
2. Підсумок других 30-ти хвилин:
Визначте, який вигляд мають функції, графік яких утворюється з графіка функції
y = g(x) шляхом виконання:
- паралельного перенесення графіка y = g(x) на 2 одиниці ліворуч;
- паралельного перенесення графіка y = g(x) на 2 одиниці вниз;
- симетрії графіка y = g(x) відносно осі абсцис;
- розтягнення графіка y = g(x) у 2 рази вздовж осі ординат;
- стиснення графіка y = g(x) у 2 рази вздовж осі абсцис.
ІІІ. Треті 30 хвилин. Робота в кабінеті математики.
1. Закріплення вивченого матеріалу.
а) напівсамостійна робота робота сильніших учнів за підручником: вправа 9.32.
б) коментоване розв’язування вправ рештою учнів:
вправа 9.23(розв’язати графічно рівняння);вправи 9.28, 9.30;
в) по черзі учні походять тестування (тест: «Функції. Перетворення графіків функцій») за програмою MyTest (на ноутбуці)
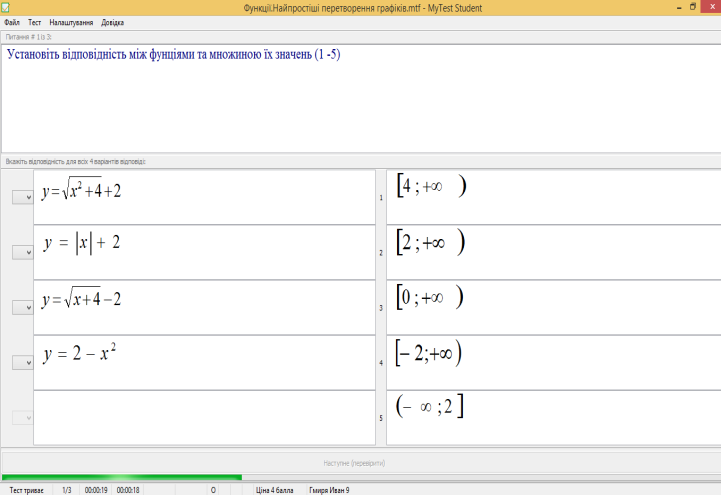
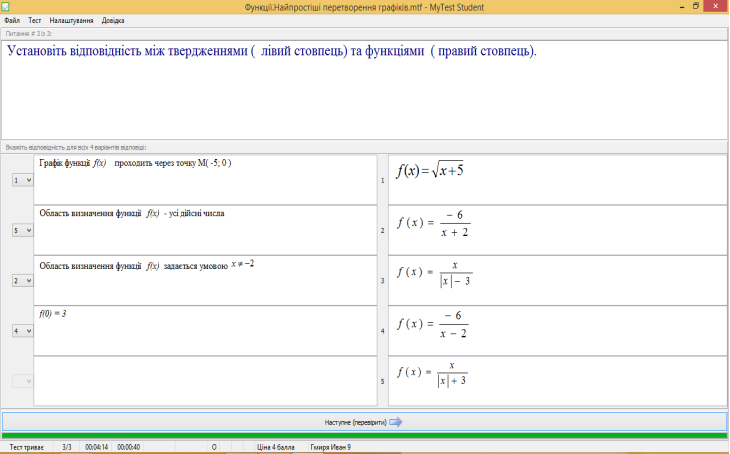
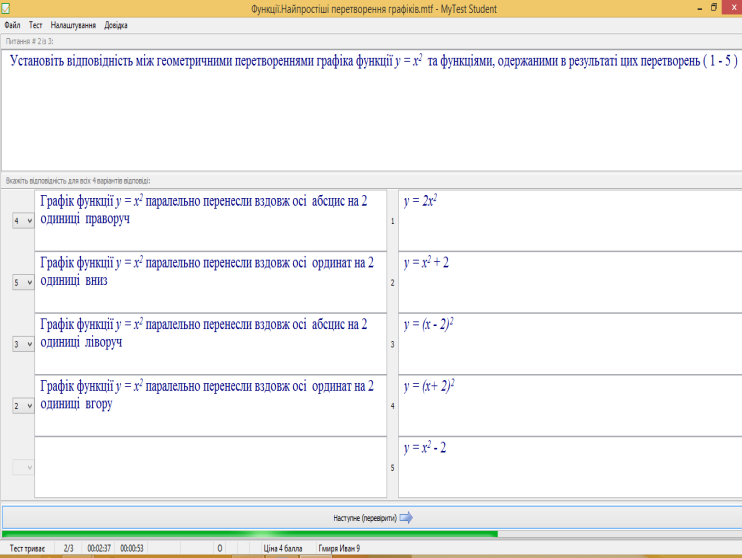
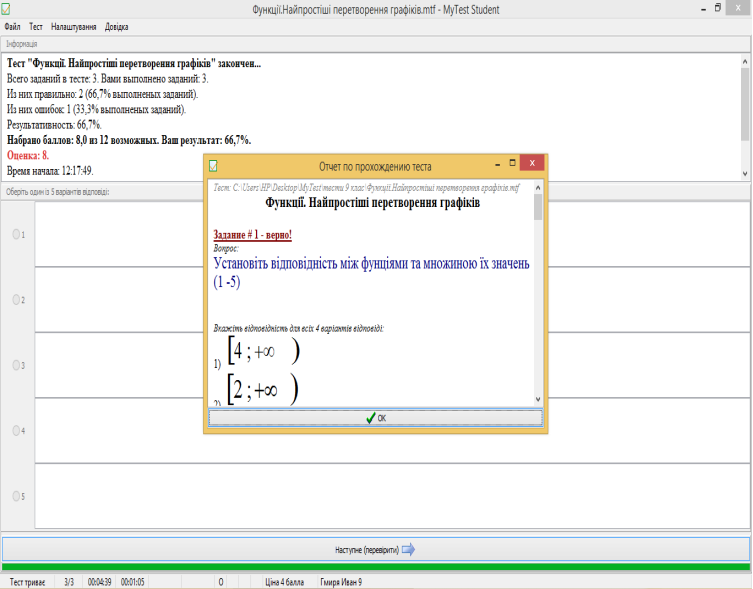
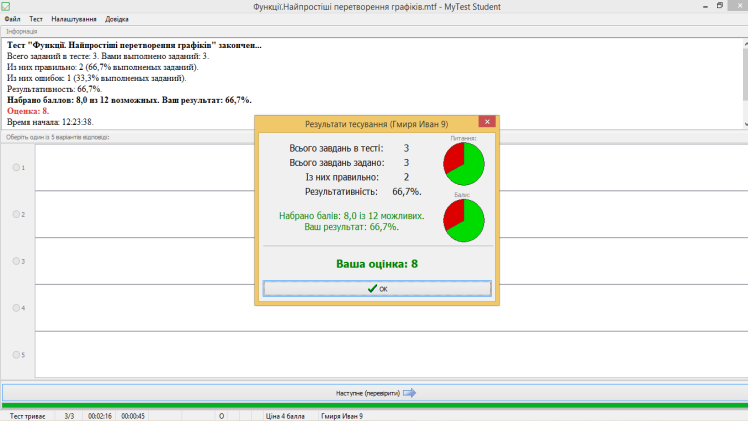
2. Підсумки уроку:
Фронтальне опитування:
Дано графіки функцій: a) y = ax; б) y = ![]() ; в) у =
; в) у = ![]() .
.
Яке рівняння буде мати функція, графік якої утвориться із даних графіків функцій:
1) при паралельному перенесенні вгору на 3 одиниці;
2) при розтягненні в 3 рази;
3) при паралельному перенесенні вправо на 3 одиниці?
3. Домашнє завдання
П.8-9(с. 70 -89) вправи: 9.16, 9.24, 9.29; тест «Функції. Перетворення графіків функцій»
Повторити: означення квадратного тричлена, формули коренів квадратного рівняння, виділення квадрата двочлена із квадратного тричлена.


про публікацію авторської розробки
Додати розробку