Урок "Найпростіші перетворення графіків функцій"

Розробка уроку з алгебри у 9 класі.

Найпростіші перетворення графіків функцій.

Мета уроку:

навчальна: сформувати вміння створення графіків функцій у = f(x+a), y = f(x)+a, y = – f(x), y = f(x) з використанням комп’ютерної програми GRAN 1, вивести основні правила перетворення графіків функції y=f(x),  удосконалити вміння учнів будувати графіки функцій, застосовуючи геометричні перетворення;

 розвивальна: розвивати логічне та творче мислення, увагу, уяву, кмітливість; формувати навички роботи з графічною інформацією, комунікативні компетенції учнів;

виховна: виховувати уважність, спостерегивість, графічну культуру, вміння самоорганізовуватися, активізувати інтерес до пізнання нового, дисциплінованість під час роботи на ПК.

Тип уроку: засвоєння нових знань.

    Форма уроку: Бінарний урок з математики та інформатики

Обладнання: Комп'ютерний клас, проектор

Програмне забезпечення  GRAN 1

Хід уроку.

1. Організаційний етап

Використання математичних процесорів для навчання дає змогу поєднати обчислювальні можливості комп’ютера у процесі дослідження різноманітних математичних залежностей, звільнити людину від рутинних обчислень, з перевагами графічного подання інформації. Для проведення уроку у комп’ютерному класі учні об’єднуються у групи.

2. Мотивація

На уроці дізнаємось, чи допоможе математичний процесор побудувати графіки функцій,  дослідити основні закономірності їх перетворення, сформулювати правила побудови функціональних залежностей.

3. Повторення опорних знань

Відкривши вікно програми GRAN 1, учні повторюють основні можливості програми при роботі з графіками (зміна кольору графіка,  кроку та одиничного відрізку).

Фронтальне опитування:

1. Яке призначення математичних процесорів?
2. Опишіть інтерфейс вікна програми GRAN1.
3. Які правила введення числових виразів у програмі GRAN1?
4. Порівняйте правила введення формул у математичному процесорі GRAN1 і табличному процесорі Excel 2007.

Пояснення вчителя:

Розглянемо загальний алгоритм побудови графіка залежності між змінними, який учні бачать на слайді:

5. Вивчення нового матеріалу

Розглянемо алгоритм побудови графіка функції на прикладах.

Завдання 1. В однієї  системі координат різними кольорами учні будують графіки функцій  

у = х²,  у = х²+2,   у = х²–2,   у = х²–3,  у = х²+1 та разом з учителем роблять висновок, що графік функції  y= f(x) + a може бути одержаний із графіка функції y= f(x) шляхом паралельного перенесення його вздовж осі ОУ на a одиниць вгору, якщо а > 0 і вниз, якщо а < 0 . Висновок учні записують в зошиті.

Завдання 2. Побудувати в одній системі координат графіки функцій  у = х²,

у = (х–2)², у = (х+2)², у =(х–3)², у = (х+1)², та роблять висновок, що графік функції  y= f(x + a) може бути одержаний із графіка функції y= f(x) шляхом паралельного перенесення його вздовж осі ОХ на а одиниць вліво, якщо а > 0 і вправо, якщо а < 0 . Висновок учні записують в зошиті.

Завдання 3. На наступному етапі  уроку вчитель пропонує учням побудувати в зошитах, використовуючи шаблон параболи у = х², графіки  функцій  у = (х+3)², у = х²–1 та у = (х+2)² +1, у = (х–1)² –2.

Завдання 4. Продовженням практичної роботи є побудова графіка функції

у = х²–2х + 3. Виконавши виділення повного квадрата ( із записами на дошці і в зошитах), учні приводять цю формулу  до вигляду  у = (х-1)²+2 та, за допомогою шаблона параболи  у = х²,  за правилами перетворень будують цей графік у себе в зошитах. Після чого перевіряють правильність побудови за допомогою програми  GRAN 1  та, змінивши колір лінії, в тій самій системі координат будують графік функції у = х² –2 х   +3. Разом з учнями вчитель робить висновок, що для побудови графіка функції y = f( x ) слід відкинути частину графіка y= f(x), яка відповідає від’ємним значенням змінної х і виконати симетрію відносно осі Оу тієї частини графіка, що відповідає додатним значенням змінної х.

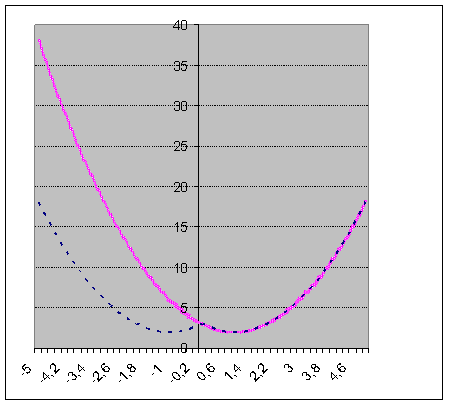
Завдання 5. Аналогічно, виконуючи на екрані комп’ютера побудови графіків функцій  у = ( х-1)², у = =( х-2)², у = ( х+1)², у =  ( х-21)²-3, учні роблять висновок,  що графік функції  y = f(x)  можна отримати із графіка функції у = f(х) , якщо виконаємо симетрію відносно осі ОХ тієї частини графіка функції у = f(х) , що міститься під цією віссю.

4. Закріплення отриманих знань.

Учні опрацьовують в групах способи побудови графіків функцій ,  та ,  . Представник кожної із груп ( не обов’язково консультант) розповідає, як побудувати один із  графіків. Учні будують ці графіки на екрані комп’ютера.

5. Рефлексія.

• Які правила перетворення графіків функцій ми сьогодні дослідили?
• Яка комп’ютерна програма нам допомогла в цьому?
• Які переваги надає математичний процесор при розв’язуванні математичних завдань?

6. Домашнє  завдання

Вивчити сформульовані правила побудови графіків за допомогою геометричних перетворень та створити графіки , , на основі графіка у = х², та   ,   на основі графіка функції .