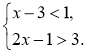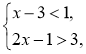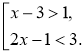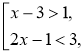Нерівність з однією змінною. Система та сукупність нерівностей з однією змінною.

Тема уроку. Нерівність з однією змінною. Система та сукупність не­рівностей з однією змінною.

Мета уроку: засвоєння учнями змісту понять: нерівність з однією змін­ною, розв'язок нерівності з однією змінною та що означає розв'язати нерівність з однією змінною; система нерівностей з однією змінною, розв'язок системи нерівностей з однією змінною та що означає розв'язати систему нерівностей з однією змінною; сукупність нерівностей з однією змінною, розв'язок сукупності нерівностей з однією змінною та що означає розв'язати сукупність нерівностей з однією змінною. Виробити в учнів уміння: відтворювати зміст вивчених понять і використовувати їх для розв'язування завдань.

Тип уроку: засвоєння знань, вироблення вмінь.

Наочність та обладнання: опорний конспект.

Хід уроку

I. Організаційний етап

Учитель повідомляє учням результати виконання тематичної контрольної роботи № 1; дає учням інформацію про орієнтовний зміст матеріалу, що пропонується до вивчення в другому розділі теми 1, та питання, які будуть винесені на контроль; налаштовує учнів на роботу.

II. Перевірка домашнього завдання

На початку уроку вчитель збирає на перевірку зошити з ви­конаним домашнім завданням (якщо таке було задано).

III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів

Для свідомого сприйняття учнями логіки навчального про­цесу вчитель може провести бесіду (або організувати відповідним чином самостійну роботу учнів з порівняння), У ході якої прово­дитимуться паралелі між поняттями «рівності» та «нерівності», а звідси цілком логічним буде перехід до понять «рівняння» та «нерівності». Таким чином учні усвідомлюють, що так само, як і у випадку з рівностями (які бувають числовими та рівностями з невідомими — рівняннями), нерівності умовно поділяють на чис­лові й такі, що містять невідомі числа, замінені буквами, значення яких треба знайти. Логічно буде після досить докладного вивчен­ня означення та властивостей числових нерівностей перейти до вивчення іншого виду нерівностей. Таким чином формулюється узагальнена мета розділу «Лінійні нерівності з однією змінною. Системи нерівностей з однією змінною» теми 1 «Нерівності». За­вдання ж уроку полягає у формуванні в учнів уявлення про зміст нових і супутніх понять.

IV. Актуалізація опорних знань та вмінь учнів

Усні вправи

1. Коли число а більше від числа b; менше від числа b? (Дайте означення, наведіть приклади.)
2. Як розміщені на координатній прямій точки, що відповідають числам а і b, якщо а 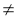b? Наведіть приклади.
3. Які нерівності називають строгими? нестрогими? Наведіть при­клади.
4. Сформулюйте властивості числових нерівностей. Наведіть при­клади.
5. Сформулюйте властивість про почленне додавання нерівностей. Наведіть приклади.
6. Сформулюйте властивість про почленне множення нерівностей. Наведіть приклади.
7. Сформулюйте наслідки з властивостей числових нерівностей. Наведіть приклади.

V. Формування знань

План вивчення нового матеріалу

1. Уявлення про нерівність з однією змінною.
2. Розв'язок нерівності з однією змінною та що означає розв'язати нерівність з однією змінною.
3. Система нерівностей з однією змінною, розв'язок системи не­рівностей з однією змінною та що означає розв'язати систему нерівностей з однією змінною.
4. Сукупність нерівностей з однією змінною, розв'язок сукупності нерівностей з однією змінною та що означає розв'язати сукуп­ність нерівностей з однією змінною.

Опорний конспект № 6

Методичний коментар

Вивчення питання про способи розв'язування нерівностей з од­нією змінною у 9 класі традиційно розпочиналося з вивчення зміс­ту поняття нерівності з однією змінною та супутніх понять, як-от: розв'язок нерівності з однією змінною та що означає розв'язати нерівність з однією змінною. Але в умовах обмеженої кількості навчальних годин, відведених програмою на вивчення другого роз­ділу, автор вважає за доцільне (на відміну від традиційної послі­довності викладення матеріалу), враховуючи подібність між озна­ченнями ключових понять, розглянути на даному уроці ще й пи­тання про зміст понять системи та сукупності нерівностей з однією змінною. Таким чином можна не тільки зекономити навчальний час, але й підготувати учнів до вивчення питання про переріз та об'єднання числових проміжків (яке вивчатиметься на наступному уроці). При формулюванні означень розв'язків нерівності з однією

змінною (а також систем і сукупностей нерівностей) особливу увагу учнів слід звернути на те, що, як і корінь рівняння, розв'язок не­рівності (або системи чи сукупності) — це число, яке перетворює дану нерівність на правильну числову нерівність.

При формуванні уявлень учнів про зміст понять системи та сукупності нерівностей слід звернути увагу учнів на те, що роз­в'язання системи передбачає пошук усіх спільних розв'язків, а розв'язання сукупності передбачає пошук таких розв'язків, які є розв'язками хоча б однієї з нерівностей. Тому спосіб дій при перевірці того, чи буде дане число розв'язком системи або, навпа­ки, сукупності нерівностей, суттєво відрізняється (див. опорний конспект № 6).

VI. Формування вмінь

Усні вправи

1. Знайдіть значення виразу:

1) 2х – 1 при х = 2; 0,2;    2) 4х + 5 при х = 2; 0,2.

2. Чи буде правильною нерівність:

1) 3х – 5 > 0 при х = -1; 2; 1; 2) 5 – 0,2х < 7 при х = 0; -10; -100?

3. Назвіть:

1) найменше ціле число, що задовольняє нерівність -2 < х < 3;

2) найменше натуральне число, що задовольняє нерівність -2 < х < 3;

3) найбільше натуральне число, що задовольняє нерівність -2 < х < 3.

4. Чи є число -3 коренем рівняння:

1) х + 3 = 0;  2) (х + 3)(x – 7) = 0;  3) х³ – 3х + 18 = 0?

Письмові вправи

Для реалізації дидактичної мети уроку учні мають розв'язати вправи такого змісту:

1. перевірити, чи є дане число розв'язком нерівності з однією змінною (або системи нерівностей, або сукупності нерівностей);
2. назвати числа певної числової множини, що є розв'язками да­ної числової нерівності;
3. на повторення: вправи на перетворення цілих виразів та на роз­в'язування лінійних рівнянь з однією змінною; вправи на засто­сування властивостей числових нерівностей з однією змінною.

Методичний коментар

Вправи, що пропонуються для розв'язання на цьому етапі уро­ку, мають сприяти закріпленню учнями знань про зміст основних понять уроку та повторенню питань, пов'язаних з числовими мно­жинами та розташуванням чисел на координатній прямій, які на наступному уроці будуть підґрунтям для вивчення понять «число­вий проміжок»; «переріз та об'єднання числових проміжків».

При розв'язуванні вправ слід постійно вимагати від учнів від­творення вивчених понять та дотримання ними правильної послі­довності дій: підставити значення змінної у нерівність (нерівності); виконавши обчислення, перевірити, чи перетвориться нерівність (нерівності) на правильну (правильні); зробити відповідний висно­вок. Таким чином ми домагаємося закріплення знань учнів з цього питання та алгоритмізуємо їхні дії.

VII. Підсумки уроку

Контрольне запитання

Яке з чисел: х = 1; х = 4; х = 5 — є розв'язком:

1) нерівності 2x – 3 < 5;  2) системи 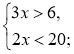 3) сукупності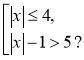

VIII. Домашнє завдання

1. Вивчити зміст понять, розглянутих на уроці (див. опорний конспект № 6) та схему дій щодо використання цих понять для розв'язування задач.
2. Виконати вправи на закріплення вивчених понять і способів дій (аналогічні за змістом вправам класної роботи).
3. На повторення: вправи на відновлення вмінь застосовувати властивості числових нерівностей та рівняння з модулем.