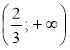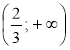Лінійні нерівності з однією змінною.
Тема уроку. Лінійні нерівності з однією змінною.
Мета уроку: домогтися засвоєння учнями змісту понять: лінійна нерівність з однією змінною, рівносильні нерівності, рівносильні перетворення нерівності та способів рівносильних перетворень нерівностей; схеми розв'язування лінійних нерівностей з однією змінною. Виробити вміння: відтворювати зміст вивчених понять та алгоритмів; виконувати дії відповідно до схеми розв'язування лінійних нерівностей з однією змінною і найпростіші рівносильні перетворення нерівностей із застосуванням властивостей числових нерівностей та наслідків із них.
Тип уроку: формування знань, вироблення первинних умінь.
Наочність та обладнання: опорний конспект № 8.
Хід уроку
I. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
Оскільки вправи домашнього завдання є вправами репродуктивного (в основному) характеру, то перевірку домашнього завдання можна здійснити або частково (тільки в учнів, що потребують додаткової педагогічної уваги), або можна запропонувати учням перевірити відповіді (правильні відповіді заздалегідь записані за дошкою або роздані як картки для самостійного опрацювання), або провести діагностичну самостійну роботу [8, самостійна робота № 3, завдання 1] з наступною перевіркою.
III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Для усвідомлення учнями необхідності вивчення нового матеріалу можна певним чином створити проблемну ситуацію: запропонувати учням спочатку виконати завдання на перевірку того, чи є дане число розв'язком нерівності з однією змінною, а потім розв'язати ту саму нерівність (нагадавши попередньо, що розв'язати нерівність означає знайти всі її розв'язки або довести, що їх немає). Усвідомлення учнями неможливості розв'язання конкретної задачі із застосуванням тих знань та вмінь, якими вони володіють, створює мотивацію до вивчення питання про види та способи розв'язування найпростіших нерівностей з однією змінною. Таким чином формулюється дидактична мета уроку, а також виділяються завдання для учнів на урок.
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
- Яке із чисел: -2; 3 — є розв'язком нерівності:
1) (х – 1)(х + 2) > 0; 2) 2х – 3 < 0?
- Чи належить проміжку [-3; 5,2) число:
1) -3; 2) 0; 3) 5; 4) 5,2; 5) 6?
- Відомо, що 5 < а < 7. Оцініть значення виразу:
1) а + 1; 2) 3а; 3) а – 3; 4) -3а; б) ![]() – 1; 6)
– 1; 6) ![]() .
.
- Спростіть вираз:
1) 4(x – 3) + 1; 2) 12 – 3(1 – 2x);
3) 5(2z + 7) + 14(5 – z); 4) х2 – 3х – 8 – х(х + 2).
- Розв'яжіть рівняння:
1) 3х = 6; 2) 0х = 0; 3) 0х = -3.
V. Формування знань
План вивчення нового матеріалу
- Поняття рівносильних нерівностей. Рівносильні перетворення нерівностей.
- Поняття лінійної нерівності з однією змінною.
- Схема розв'язування лінійної нерівності з однією змінною.
- Як розв'язати нерівність з однією змінною, що зводиться до лінійної. Приклади.
Методичний коментар
Відповідно до даного плану викладання матеріалу формування знань учнів на даному уроці розпочинається з вивчення означення рівносильних нерівностей з однією змінною і продовжується вивченням формулювань основних теорем рівносильності (які даються без доведення та пояснюються на прикладах). Для кращого розуміння учнями цього фрагменту матеріалу уроку можна запропонувати їм порівняти властивості числових рівностей та нерівностей і таким чином виявити як схожі, так і відмінні їхні риси. Результатом такого порівняння буде усвідомлення учнями існування певних аналогій між поняттями «рівняння та його розв'язання» і «нерівність і її розв'язання» та засобів розв'язування як одних, так і інших (та акцентувати увагу на відмінностях — при множенні або діленні обох частин нерівності на від'ємне число). Звернемо увагу, що в різних джерелах означення лінійної нерівності з однією змінною даються дещо по-різному: у традиційних підручниках останніх років це нерівність виду ax > b (ax < b, ах ≥ b, ах ≤ b), а наприклад, у таблицях з алгебри для 7—11 класів [7] це нерівність виду ax + b > 0 (ax + b < 0, ax + b ≥ 0, ax + b ≤ 0). Учням можна продемонструвати обидва означення і показати, що відмінність першого полягає тільки в тому, що описувану нерівність уже зведено до виду, аналогічного виду лінійних рівнянь з однією змінною (ах = b).
Порівнюючи лінійні нерівності з однією змінною та лінійні рівняння з однією змінною, слід зауважити, що з огляду на існуючу відмінність рівносильної властивості (див. множення або ділення обох частин нерівності на те саме від'ємне число), залежно від знака нерівності, можна скласти не одну схему розв'язування лінійної нерівності з однією змінною (особливо це стосується випадку, коли число а дорівнює 0), тому акцент треба робити не на заучуванні схем, а на розумінні дій, які скриті за цими схемами).
Завершальний етап вивчення нового матеріалу є практичною частиною (яка може бути подана як відповідь на запитання, поставлене на початку уроку): на прикладі нерівності з однією змінною під час коментування складається орієнтовна схема дій при розв'язуванні нерівності з однією змінною, що зводиться до лінійної. Під час коментування також доречним буде проведення паралелей з розв'язуванням відповідного рівняння з однією змінною.
Опорний конспект № 8
|
Дві нерівності називають рівносильними, якщо вони мають ті самі розв'язки. |
|
|
Деякі рівносильні перетворення нерівностей |
|
|
1. Якщо з однієї частини нерівності перенести в іншу частину доданки з протилежними знаками, то утвориться нерівність, рівносильна даній. Наприклад: 2x – 3 > 6 і 2х > 9 —рівносильні нерівності. |
|
|
2. Якщо обидві частини нерівності помножити (або поділити) на те саме додатне число, то утвориться нерівність, рівносильна даній.
Наприклад: 2x > 6 і х > 3, |
|
|
3. Якщо обидві частини нерівності помножити (поділити) на те саме від'ємне число і змінити знак нерівності на протилежний, то утвориться нерівність, рівносильна даній. |
|
|
Наприклад: -3х > 6 і х < -2; |
|
|
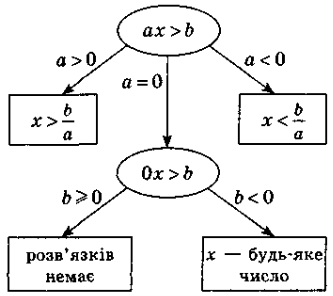
Лінійна нерівність з однією змінною — нерівність виду ах > b, або ах < b, або ах ≥ b, або ах ≤ b, де а, b — дані числа, ах — змінна. Наприклад: 3х > 1; -x < -3; 0х > 3; 0х < 0 —лінійні нерівності. |
|
|
Схема розв'язування лінійної нерівності |
|
|
|
|
|
Приклад розв'язування нерівності, що зводиться до лінійної: |
|
|
Розв'язати нерівність 9(х – 1) + 5х < 17х – 11 |
Коментар |
|
9х – 9 + 5х < 17х – 11 14х – 9 < 17х – 11 |
1. Виконаємо тотожні перетворення лівої (і правої) частин нерівності. |
|
14х – 17х < -11 + 9 -3х < -2 |
2. Перенесемо відомі доданки в одну частину нерівності, а невідомі — в іншу. Тотожно перетворимо обидві частини. |
|
х >
x
Відповідь: |
3. Оскільки коефіцієнт при х у лівій частині утвореної нерівності не дорівнює нулю, поділимо на нього обидві частини нерівності, змінивши її знак на протилежний (бо -3 < 0). Запишемо відповідний числовий проміжок — це і є відповідь — розв'язок даної нерівності. |
VI. Формування вмінь
Усні вправи
-
Визначте й обґрунтуйте, чи рівносильні дані нерівності.
1) 3х > 3 і х > 3; 2) 3х > 3 і х > 1;
3) 3 + х > 5 і х > 5; 4) 3 + х > 5 і х > 2.
- Розв'яжіть нерівність:
1) 3х > 3; 2) х + 3 > 5; 3) -3х > 3; 4) х – 3 > 5;
5) –х < 6; 6) 0х < 7; 7) 0х > 7.
- Спростіть вираз:
1) 8х – (х + 2); 2) 8х – 5(х + 2); 3) 9(х – 3) – 5(х + 2).
Письмові вправи
Для реалізації дидактичної мети уроку слід розв'язати вправи такого змісту:
- перевірити, чи є дані дві нерівності рівносильними (використавши властивості рівносильності нерівностей);
- розв'язати нерівності з однією змінною, що зводяться до лінійних нерівностей з однією змінною шляхом застосування одного з вивчених рівносильних перетворень;
- розв'язати нерівності з однією змінною, що зводяться до лінійних нерівностей з однією змінною шляхом застосування кількох (або всіх) вивчених рівносильних перетворень;
- на повторення: рівняння з однією змінною, що зводяться до лінійних рівнянь з однією змінною шляхом попереднього множення (або ділення) обох частин рівняння на те саме число — найменший спільний знаменник усіх дробів (або найбільший спільний дільник усіх коефіцієнтів).
Методичний коментар
Розв'язання вправ на цьому етапі уроку слід розпочати з вправ, що сприяють закріпленню учнями змісту понять «рівносильні нерівності» та «рівносильні перетворення нерівностей». При цьому в процесі розв'язування таких вправ слід вимагати від учнів свідомого коментування своїх дій з використанням вивченої термінології.
Наступна група завдань має на меті сприяти закріпленню в учнів знань щодо схеми розв'язування лінійних нерівностей з однією змінною та виробленню в учнів сталих умінь як розв'язувати лінійні нерівності з однією змінною, так і виконувати рівносильні перетворення нерівностей з однією змінною.
Тільки переконавшись у тому, що основні навички розв'язування найпростіших нерівностей з однією змінною в учнів вироблено, можна переходити до більш складних прикладів, які сприяють вдосконаленню навичок тотожних перетворень.
Щоб підготувати учнів до сприйняття матеріалу наступного уроку (розв'язування нерівностей, що містять дроби з числовими знаменниками), на даному уроці учням пропонується кілька прикладів на повторення: на розв'язування рівнянь відповідного виду.
VII. Підсумки уроку
Контрольні запитання
- Які дві нерівності називають рівносильними?
- Як (якими способами) можна з даної нерівності (з однією змінною) утворити рівносильну їй нерівність?
- Нерівності якого виду називають лінійними нерівностями з однією змінною? Наведіть приклади.
- Які розв'язки може мати нерівність ах > b, якщо:
1) а > 0; 2) а < 0; 3) а = 0, b > 0; 4) а = 0, b < 0?
VIII. Домашнє завдання
- Вивчити зміст тверджень, розглянутих на уроці (див. опорний конспект № 8).
- Розв'язати вправи на закріплення змісту поняття «рівносильні перетворення нерівностей» і на вироблення вмінь розв'язувати лінійні нерівності з однією змінною та такі, що зводяться до лінійних шляхом найпростіших рівносильних перетворень (аналогічні за змістом та рівнем складності вправам класної роботи).
- На повторення: розв'язати рівняння (аналогічні розв'язаним у вправах на повторення — див. класну роботу) та розв'язати вправи на знаходження ОДЗ раціональних виразів.

про публікацію авторської розробки
Додати розробку