НМТ-2023. Завдання та розв'язки

НМТ-2023демонстраційний варіантhttps://terletskyi.blogspot.com

Завдання з вибором однієї правильної відповіді

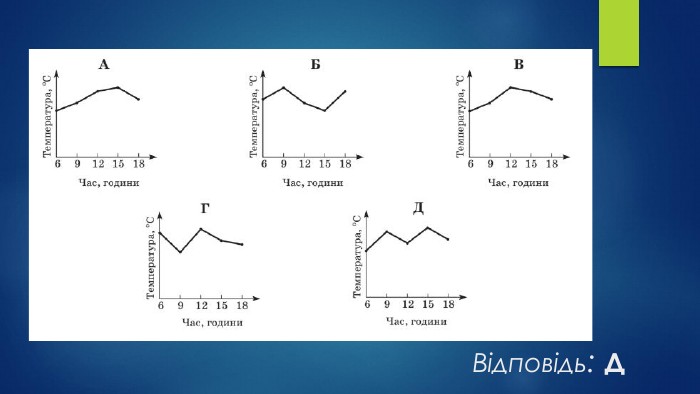
1. У таблиці наведено дані про температуруповітря в різний час того самого дня. На графіках немає шкали (градації)температури повітря. На якому графікуправильно відображені дані, наведені втаблиці?{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}Час, години69121518 Температура, 0 С1217141815

Відповідь: Д

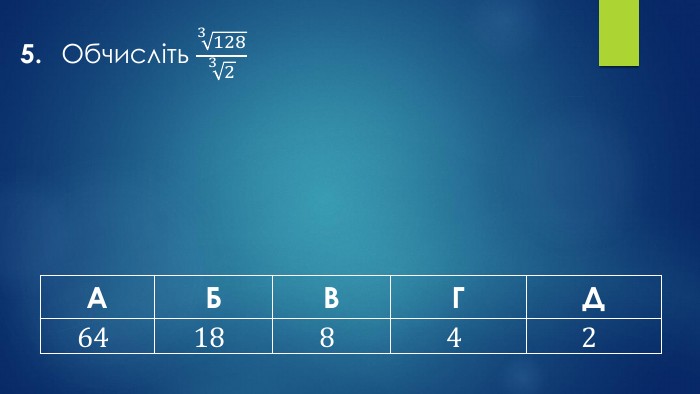
2. У супермаркеті проходить акція: купуєш триоднакові шоколадки «Спокуса» - таку самучетверту супермаркет надає безкоштовно. Ціна кожної такої шоколадки – 35 грн. Покупецьмає у своєму розпорядженні – 220 грн. Якумаксимальну кількість шоколадок «Спокуса»він зможе отримати, взявши участь у акції?{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД56789{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД

Відповідь: Г220:35=6 10 в остачі. Отже можна купити 6 шоколадок. 6:3=2. Таким чином покупець отримає2 бонусні шоколадки.6+2=8 Розв’язання

3. Визначте кількість граней трикутної призми{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД34569{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД

Відповідь: ВРозв’язання3 бічних грані+2 основи 

4. У прямокутному трикутнику сума двох кутівдорівнює 1150. Визначте градусну мірунайменшого кута цього трикутника  {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД50150250350650{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД

Відповідь: ВРозв’язання1150−900=250−один з кутів900−250=650−інший кут 

5. Обчисліть 312832 {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД6418842{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД

Відповідь: ГРозв’язання312832=31282=364=343=4 

6. Яке з наведених чисел є коренем рівняння 𝑥2+𝑥3=2 {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД0,41,22,4512{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД

Відповідь: ВРозв’язання𝑥2+𝑥3=2 ∙6,3𝑥+2𝑥=12,5𝑥=12,𝑥=12:5,𝑥=2,4. 

7. Укажіть лінійну функцію, графік якоїпаралельний осі абсцис і проходитьчерез точку А(−2;3)  А 𝑦=3 Б 𝑦=−2 В 𝑥=−2 Г 𝑥=3 Д 𝑦=−32𝑥 Відповідь: А

8. Обчисліть значення виразу log28𝑎, якщоlog2𝑎=4 {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД675812{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД

Відповідь: БРозв’язанняlog28𝑎=log28+log2𝑎==log223+log2𝑎=3log22+log2𝑎==3+log2𝑎log2𝑎=4=>log28𝑎=3+4=7 

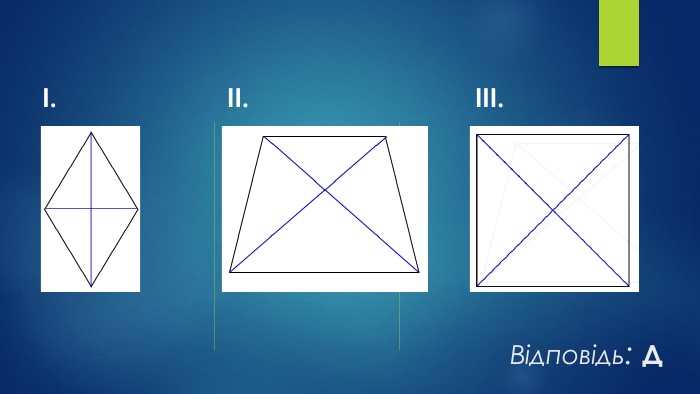
9. Які з наведених тверджень є правильними?I. Діагоналі будь-якого ромба ділять йогокути навпіл. II. Діагоналі будь-якого чотирикутника точкаперетину ділить навпіл. III. Діагоналі будь-якого квадрата взаємноперпендикулярні.{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГДлише ІІ, ІІ та ІІІлише ІІІлише І та ІІлише І та ІІІ

Відповідь: ДІ.ІІ.ІІІ.

10. Спростіть вираз 𝑎2+16𝑎−4−8𝑎𝑎−4 {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД−1𝑎−4𝑎+41𝑎−42{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД

Відповідь: БРозв’язання𝑎2+16𝑎−4−8𝑎𝑎−4=𝑎2+16−8𝑎𝑎−4==𝑎2−8𝑎+16𝑎−4=𝑎−42𝑎−4=𝑎−4 

11. Розв’яжіть систему рівнянь 13𝑥<81,𝑥≤5. {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД−∞;45;+∞−5;−4−4;5−5;4{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД

Відповідь: ГРозв’язання13𝑥<81,𝑥≤5;=>3−𝑥<34,−5≤𝑥≤5;=>=>−𝑥<4,−5≤𝑥≤5;= >𝑥>−4,−5≤𝑥≤5;=>=>−4<𝑥≤5 

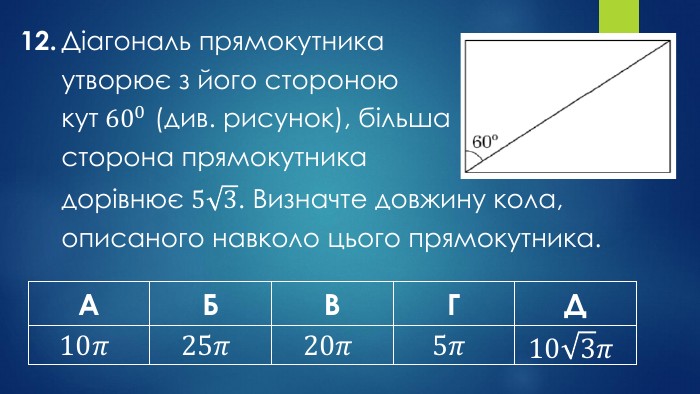
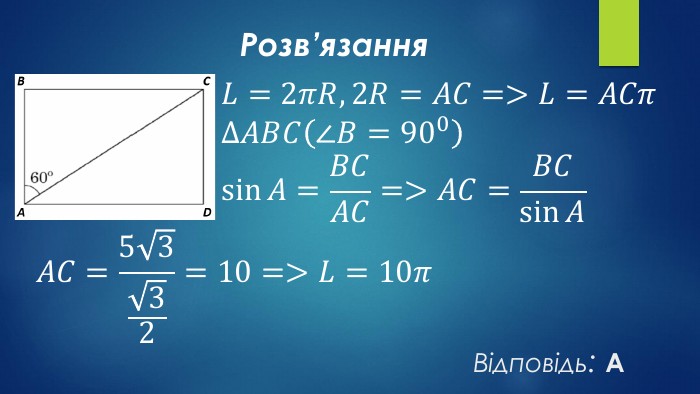
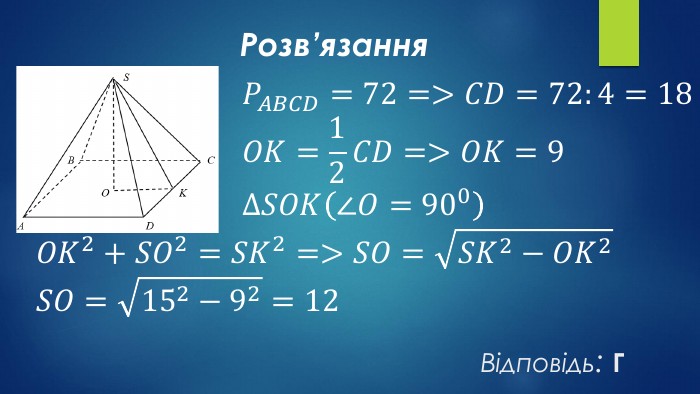
12. Діагональ прямокутникаутворює з його стороноюкут 600 (див. рисунок), більшасторона прямокутникадорівнює 53. Визначте довжину кола,описаного навколо цього прямокутника. {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД10𝜋25𝜋20𝜋5𝜋103𝜋{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД

Відповідь: АРозв’язання𝐿=2𝜋𝑅,2𝑅=𝐴𝐶=>𝐿=𝐴𝐶𝜋∆𝐴𝐵𝐶∠𝐵=900sin𝐴=𝐵𝐶𝐴𝐶=>𝐴𝐶=𝐵𝐶sin𝐴𝐴𝐶=5332=10=>𝐿=10𝜋 

13. В арифметичній прогресії 𝑎1=4,𝑎2=−1. Укажіть формулу для визначення 𝑛−гочлена цієї прогресії.  А 𝑎𝑛=9−5𝑛Б 𝑎𝑛=7−3𝑛В 𝑎𝑛=5−𝑛Г 𝑎𝑛=1+3𝑛Д 𝑎𝑛=−1+5𝑛 

Відповідь: АРозв’язання𝑎𝑛=𝑎1+𝑑𝑛−1,𝑑=𝑎2−𝑎1=>𝑑=−1−4=−5.𝑎𝑛=4−5𝑛−1=4−5𝑛+5=9−5𝑛. 

14. Периметр основи правильноїчотирикутної піраміди дорівнює 72 см. Визначте довжину висоти піраміди, якщоїї апофема дорівнює 15 см. {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД6 см9 см10 см12 см14 см{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД

Відповідь: ГРозв’язання𝑃𝐴𝐵𝐶𝐷=72=>𝐶𝐷=72:4=18𝑂𝐾=12𝐶𝐷=>𝑂𝐾=9∆𝑆𝑂𝐾∠𝑂=900𝑂𝐾2+𝑆𝑂2=𝑆𝐾2=>𝑆𝑂=𝑆𝐾2−𝑂𝐾2𝑆𝑂=152−92=12 

15. Укажіть корінь рівняння sin𝑥=32 напроміжку 0;3𝜋 {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГДжодногоодиндватрибільшетрьох{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД

Відповідь: ДРозв’язанняsin𝑥=32=>𝑥=−1𝑘𝜋3+𝜋𝑘,𝑘∈𝑍.𝑘=0=>𝑥=𝜋3,𝑘=1=>𝑥=−𝜋3+𝜋=2𝜋3,𝑘=2=>𝑥=𝜋3+2𝜋=7𝜋3,𝑘=3=>𝑥=−𝜋3+3𝜋=8𝜋3. 

Завдання на встановлення відповідності

16. Доберіть до функції (1–3) ескіз її графіка (А–Д).

Функція1 𝑦=tg𝑥2 𝑦=12𝑥3 𝑦=1𝑥 Відповідь: 1–Г,2–Д,3–А

17. Доберіть до запитання (1–3) правильнувідповідь до нього (А–Д). Запитання Відповідь до запитання1 Яке число є дільником 8? А 82 Яке число є простим? Б 16 3 Яке число є квадратом В 17 натурального числа? Г 27 Д 56  

Відповідь: 1–А,2–В,3–БРозв’язання1. 8:8=12. 17:1=17, 17:17=13. 16=42 

18. На рисунку зображено відрізок 𝑑 накоординатній площині. Установітьвідповідність між відрізком (1–3) та рисунком(А–Д), на якому він зображений. 

Відрізок1 відрізок, симетричний відрізку 𝑑 відносно oсі 𝑥 2 відрізок, симетричний відрізку 𝑑 відносно осі 𝑦3 відрізок, симетричний відрізку 𝑑 відносно точки 𝑂 Відповідь: 1–Б,2–Г,3–Д

Завдання відкритої форми з короткою відповіддю

19. Обчисліть 07𝑓𝑥𝑑𝑥, використавшизображений на рисунку графік лінійноїфункції 𝑦=𝑓𝑥 

Відповідь: 38,5 Розв’язання07𝑓𝑥𝑑𝑥=𝑆𝐴𝐵𝐶𝐷𝑆𝐴𝐵𝐶𝐷=𝐴𝐵+𝐶𝐷2∙𝐴𝐷𝐴𝐵=3,𝐶𝐷=8,𝐴𝐷=7𝑆𝐴𝐵𝐶𝐷=3+82∙7=38,5 

20. Михайло отримав з математики в першомусеместрі такі оцінки: «8», «7», «9», «8». Якукількість оцінок «10» протягом цього семестру треба отримати Михайлові зматематики, щоб середнє арифметичневсіх отриманих у першому семестрі оцінокіз цього предмета дорівнювало 9,5?Уважайте, що інших оцінок із математики,окрім «10», Михайло не отримуватиме.

Відповідь: 12 Розв’язання𝑥=𝑥1+𝑥2+…+𝑥𝑛𝑛9,5=8+7+9+8−10𝑥4+𝑥9,54+𝑥=32+10𝑥,38+9,5𝑥=32+10𝑥,9,5𝑥−10𝑥=32−38,−0,5𝑥=−6,𝑥=12. 

20. Об’єм конуса дорівнює 64 см3. Черезсередину висоти цього конуса паралельнойого основі проведено площину. Утворенийпереріз є основою меншого конуса,вершина якого збігається з вершиноюзаданого. Обчисліть об’єм см3 меншогоконуса. 

Відповідь: 8 Розв’язання𝑉=13𝜋𝑂𝐴2∙𝑆𝑂,𝑉1=13𝜋𝑂1𝐴12∙𝑆𝑂1𝑆𝑂1=12𝑆𝑂,𝑂1𝐴1=12𝑂𝐴𝑉1=13𝜋12𝑂𝐴2∙12𝑆𝑂=13𝜋∙14𝑂𝐴2∙12𝑆𝑂==18∙13𝜋𝑂𝐴2∙𝑆𝑂=18∙𝑉=>=>𝑉1=18∙64=8 

22. Визначте найменше ціле значення 𝑎, заякого корені рівнянняlog22𝑥−𝑎−1log2𝑥−𝑎=0належать проміжку 30;100. 

Розв’язанняlog22𝑥−𝑎−1log2𝑥−𝑎=0,log2𝑥=𝑡,𝑡2−𝑎−1𝑡−𝑎=0,𝐷=𝑎−12−4∙1∙−𝑎=𝑎2−2𝑎+1+4𝑎==𝑎2+2𝑎+1=𝑎+12𝑡1=𝑎−1−𝑎+12∙1=𝑎−1−𝑎−12=−1,𝑡2=𝑎−1+𝑎+12∙1=2𝑎2=𝑎 

Розв’язанняlog2𝑥=𝑎= >𝑥=2𝑎30<𝑥<100,30<2𝑎<100. Очевидно, що 𝑎=5, оскільки 25=32 Відповідь: 5

P. S. НМТ-2023. 20 презентацій (не офіційнізавдання) та багато інших матеріалів дляпідготовки до ЗНО і не тільки.https://terletskyi.blogspot.com/p/blog-page_93.html https://terletskyi.blogspot.com