Презентація "Нумерація різних народів світу. Дробі."

Нумерація різних народів світу. Підготувала Артьомова Аліна Вадимівна

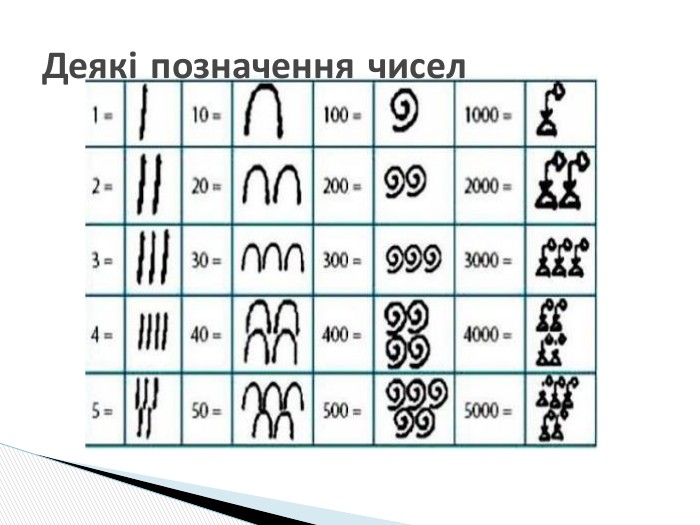
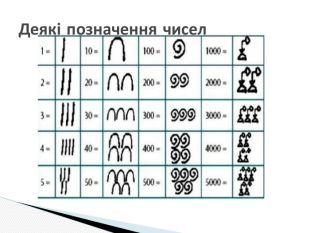
Єгипетська система числення — непозиційна система числення, яка вживалася в Стародавньому Єгипті аж до початку X ст. У цій системі цифрами були ієрогліфічні символи; вони позначали числа 1, 10, 100 і т. д. до мільйона. Числа, не кратні 10, записувалися шляхом повторення цих цифр. Кожна цифра могла повторюватися від одного до 9 разів. Єгипетська система числення

Числа мали такі позначення

Деякі позначення чисел

Вавилонські цифри — цифри, що використовувалися вавилонянами в своїй шістдесятковій системі числення. Записувалися клинописом на глиня-них табличках. Поки глина ще м'яка, дерев'яною паличкою для письма або загостреним очеретом видавлювали знаки. Нумерація давніх вавилонян

Вавилоняни, які славилися своїми астрономічними спостереженнями та розрахунками (за допомогою свого винаходу абака), успадкували від шумерської й аккадської цивілізацій шістдесяткову систему числення. Вона застосовувалася за дві тисячі років до н.е. Для запису чисел використовувалися всього два знаки: прямий клин  для позначення одиниць і лежачий клин  для позначення десятків всередині шістдесяткового розряду. Запис чисел у вавилонян

Новий шістдесятковий розряд починався з появою прямого клина після лежачого клина, якщо розглядати число справа наліво. Таким чином, число зображувалося в позиційній 60-річній системі, а його 60-кові цифри — в адитивній десятковій. Аналогічно записувалися дроби. Для популярних дробів 1/2, 1/3 і 2/3 були спеціальні значки.

Спочатку нуля не було. Згодом запровадили позначення для пропущених шестидесяткових розрядів, що відповідає появі нуля, але в першому розряді праворуч цей знак не ставився, що призводило до неоднозначності запису чисел. І для визначення абсолютного значення числа були потрібні додаткові відомості. 

Алфавітні нумерації

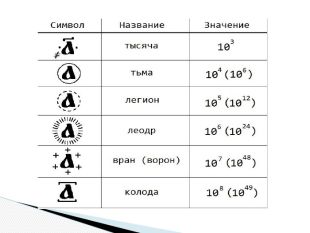
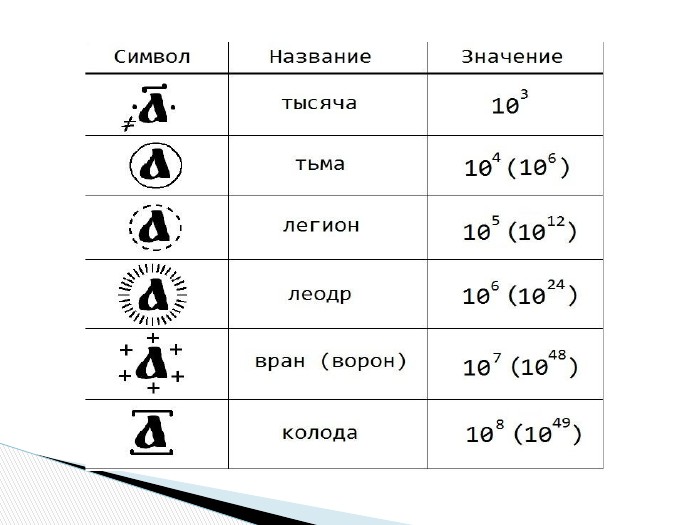
Найдосконалішими серед непозиційних систем були алфавітні позначення чисел. Слов'янське алфавітне позначення чисел виникло в X ст. і застосовувалося без істотних змін до XVII ст. включно. Над буквою, яка позначала певне число, ставили особливий знак — титло. Для позначення багатоцифрових чисел знаки записували підряд: тисячі, сотні, десятки, одиниці. Слов'янська алфавітна нумерація була десятковою.

Римська нумерація виникла, як випливає з назви, в Стародавньому Римі. Існує сім основних символів: I, V, X, L, C, D і M. Вперше ці символи почали використовувати між 900 і 800 роками до н. е. Цифри були розроблені для використання в якості загального методу підрахунку, необхідного для розвитку відносин і торгівлі. Підрахунок пальців виходив з-під контролю, так би мовити, коли за рахунку доходили до 10. Римська нумерація

Вважається, що система підрахунку була розроблена на основі руки людини. Одна лінія, або I, символізує одну штуку чого-небудь, або, відповідно, один палець. V був зображенням п'яти пальців, зокрема V-подібну форму, зроблену великим і вказівним пальцями. X відповідав двом рукам (з'єднані в одній точці, вони утворюють дві V). M = 1000. Спочатку це значення представляла грецька буква phi - Φ. Іноді воно уявлялося як C, I і зворотна C: CIƆ, що віддалено схоже на М. Дослідники вважають збігом, що латинське слово mille використовується для позначення тисячі.

Однак точне походження цих цифр римської нумерації неясно. При цьому зміни в їх формах з III століття до нашої ери добре відомі. Представлене вище походження римських цифр засноване на теорії історії римської нумерації німецького вченого Теодора Моммсена (1850), що отримала широке визнання. Однак вивчення написів, залишених етрусками, які правили Італією до латинян, показує, що римляни взяли етруську чисельну систему, починаючи з V століття до нашої ери. Але є і зовсім різні: етруски читали свої числа справа наліво, а римляни читали їх зліва направо.

Ці цифри не позбавлені недоліків. Наприклад, немає символу, що позначає нуль, також немає можливості розрахувати дріб. Це ускладнювало можливість розвитку загальноприйнятої складної математичної системи, ускладнювало торгівлю. В кінцевому рахунку римські цифри поступилися місцем більш універсальній арабськії системі, де числа читаються як одне число в послідовності. Наприклад, 435 як чотири сотні тридцять п'ять. Недоліки римської системи нумерації

Одним з найбільш складних розділів математики донині вважаються дроби. Історія дробів налічує не одне тисячоліття. Уміння ділити ціле на частини виникло на території стародавнього Єгипту та Вавилону. З роками ускладнювалися операції з дробами, змінювалася форма їх запису. У кожної держави стародавнього світу були свої особливості у «взаєминах» з цим розділом математики. Сьогодні розрізняють два способи їх запису. Звичайні та десяткові дроби виникли в різний час: перші є більш давніми. Виникнення і розвиток звичайних дробів

Коли виникла необхідність ділити ціле на частини без зайвих зусиль, тоді і з'явилися дроби. Історія дробів нерозривно пов'язана з вирішенням утилітарних завдань. Сам термін «дріб» має арабське коріння і походить від слова, що означає «ламати, розділяти». З давніх часів у цьому сенсі мало що змінилося. Сучасне визначення звучить наступним чином: дріб — це частина або сума частин одиниці. Відповідно, приклади з дробами являють собою послідовне виконання математичних операцій з частками чисел.

Види звичайних дробів сьогодні включають в себе і так звані єгипетські. Вони являють собою суму кількох доданків виду 1/n. Чисельник — завжди одиниця, а знаменник — натуральне число. З'явилися такі дроби, як не важко здогадатися, у стародавньому Єгипті. При розрахунках усі частки намагалися записувати у вигляді таких сум (наприклад, 1/2 + 1/4 + 1/8).

Окремими позначеннями володіли тільки дроби 2/3 та ¾, інші розбивалися на складові. Існували спеціальні таблиці, в яких частки числа представлялися у вигляді суми. Найдавніша з відомих згадок такої системи зустрічається у Математичному папірусі Рінда, датованому початком другого тисячоліття до нашої ери. Він включає таблицю дробів і математичні задачі з рішеннями і відповідями, поданими у вигляді сум дробів. Єгиптяни вміли складати, ділити і множити частки числа

Дроби в долині Нілу записувалися за допомогою ієрогліфів. Подання частки числа у вигляді суми доданків виду 1/n, характерну для стародавнього Єгипту, використовувалося математиками не тільки цієї країни. Аж до Середніх століть єгипетські дробу застосовувалися на території Греції та інших держав.

Система числення у Вавилоні була шістдесяткова. Кожен новий розряд відрізнявся від попереднього на 60. Така система збереглася в сучасному світі для позначення часу і величин кутів. Дроби також були шестидесяткові. Для запису використовували спеціальні значки. Як і в Єгипті, приклади з дробами містили окремі символи для позначення 1/2, 1/3 і 2/3. Вавилонська система не зникла разом з державою. Дробами, написаними в 60-тирічній системі, користувалися античні і арабські астрономи і математики.

Історія звичайних дробів мало чим збагатилася в стародавній Греції. Жителі Еллади вважали, що математика повинна оперувати лише цілими числами. Тому вирази з дробами на сторінках давньогрецьких трактатів практично не зустрічалися. Проте певний внесок у цей розділ математики внесли піфагорійці. Вони розуміли дроби як відношення або пропорції, а одиницю вважали також неподільною. Піфагор з учнями побудував загальну теорію дробів, навчився проводити всі чотири арифметичні операції, а також порівняння дробів шляхом приведення їх до спільного знаменника. Дроби в Греції

Римська система дробів була пов'язана з мірою ваги, званої «асс». Вона ділилася на 12 часток. 1/12 асса називалася унцією. Для позначення дробів існувало 18 назв. Наведемо деякі з них: семис — половина асса; секстанте — шоста частка асса; семиунция — пів-унції або 1/24 асса. Незручність такої системи полягала в неможливості подати число у вигляді дробу зі знаменником 10 або 100. Римські математики подолали труднощі з допомогою використання відсотків. Римська система дробів

В Античності дроби вже писали знайомим нам чином: одне число над іншим. Однак була одна істотна відмінність. Чисельник розташовувався під знаменником. Вперше так писати дроби почали в стародавній Індії. Сучасний нам спосіб почали використовувати араби. Але ніхто з названих народів не застосовував горизонтальну риску для поділу чисельника і знаменника. Вперше вона з'являється в працях Леонардо Пізанського, більш відомого як Фібоначчі, в 1202 році. Написання дробів.

Якщо історія виникнення звичайних дробів почалася в Єгипті, то десяткові вперше з'явилися в Китаї. У Піднебесній імперії їх стали використовувати приблизно з III століття до нашої ери. Історія десяткових дробів почалася з китайського математика Лю Хуэя, який запропонував використовувати їх при добуванні квадратних коренів. У III столітті нашої ери десяткові дроби в Китаї стали застосовуватися при розрахунку ваги та об'єму. Поступово вони все глибше почали проникати в математику. У Європі, однак, десяткові дроби стали застосовуватися набагато пізніше. Десяткові дроби

Незалежно від китайських попередників десяткові дроби відкрив астроном аль-Каші з древнього міста Самарканда. Жив і працював він в XV столітті. Свою теорію вчений виклав у трактаті «Ключ арифметики», що побачив світло в 1427 році. Аль-Каші запропонував використовувати нову форму запису дробів. І ціла і дробова частина тепер писалися в одному рядку. Для їх поділу самаркандський астроном не використовував кому. Він писав ціле число і дробову частину різними кольорами, використовуючи чорні і червоні чорнило. Іноді для поділу аль-Каші також застосовував вертикальну риску. Аль-Каші з Самарканда

Новий вид дробів почав з'являтися в працях європейських математиків з XIII століття. Потрібно зауважити, що з працями аль-Каші, як і з винаходом китайців вони знайомі не були. Десяткові дроби з'явилися в працях Йордану Неморарія. Потім їх використовував вже в XVI столітті Франсуа Вієт. Французький вчений написав «Математичний канон», в якому містилися тригонометричні таблиці. У них Вієт при доведенні використовував десяткові дроби. Десяткові дроби в Європі

Для розділення цілої і дробової частини вчений застосовував вертикальну риску, а також різний розмір шрифту. Проте це були лише окремі випадки наукового використання. Для вирішення повсякденних завдань десяткові дроби в Європі стали застосовуватися дещо пізніше. Сталося це завдяки голландському вченому Симону Стевину в кінці XVI століття. Він видав математичну працю «Десята» в 1585 році. У ній вчений виклав теорію використання десяткових дробів в арифметиці, у грошовій системі і для визначення мір і ваг.