КОНСПЕКТ УРОКУ «КУЛЯ І СФЕРА»

Про матеріал

Тема уроку. Куля і сфера. Взаємне розміщення площини і кулі (сфери) у просторі. Мета уроку: формування понять куля, сфера, центр кулі, радіус кулі, діаметр кулі, діаметрально протилежні точки та вмінь учнів знаходити елементи кулі (сфери) й визначати взаємне розміщення площини і кулі (сфери) у просторі.

Перегляд файлу

КОНСПЕКТ УРОКУ «КУЛЯ І СФЕРА»

Тема уроку. Куля і сфера. Взаємне розміщення площини і кулі (сфери) у просторі.

Мета уроку: формування понять куля, сфера, центр кулі, радіус кулі, діаметр кулі, діаметрально протилежні точки та вмінь учнів знаходити елементи кулі (сфери) й визначати взаємне розміщення площини і кулі (сфери) у просторі.

Обладнання: моделі куль та сфер. І. Перевірка домашнього завдання

Наприкінці уроку збираються учнівські зошити для перевірки виконання домашнього завдання і ведення зошитів.

II. Аналіз виконання тематичного оцінювання № 3

Повідомити загальний результат виконання роботи та проаналізувати її. III. Сприйняття та усвідомлення нового матеріалу

Куля та сфера

Кулею називається тіло, утворене обертанням круга навколо його діаметра. Сферою називається фігура, утворена обертанням кола навколо його діаметра.

Демонструємо моделі куль та сфер. Можна дати інші означення сфери і кулі.

Сферою називається поверхня, яка складається із всіх точок простору, що знаходяться на даній відстані (яка називається радіусом) від даної точки (яка називається центром).

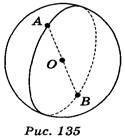Відрізок, який з'єднує центр сфери з точкою сфери, називається радіусом сфери. Відрізок, який з'єднує дві точки сфери і проходить через центр сфери, називається діаметром сфери. На рис. 135 точка О — центр сфери, ОА, OB — радіуси сфери, АВ — діаметр сфери.

Кулею називається тіло, яке складається із всіх точок

простору, які знаходяться на відстані не більшій даної (яка називається радіусом кулі) від даної точки (яка називається центром кулі).

Площина, яка проходить через центр кулі (сфери), називається діаметральною площиною. Переріз кулі (сфери) діаметральною площиною називається великим кругом (великим колом).

Розв'язування задач

1. Радіус кулі дорівнює 2 см. Всередині чи поза кулею розміщена точка А, якщо вона віддалена: а) від центра кулі на 1 см; б) від центра кулі на 1,5 см;

в) від точки на поверхні кулі на 3 см?

2. Знайдіть площу великого круга і довжину великого кола, якщо його радіус дорівнює 2 см. (Відповідь. 4π см²; 4π см.)

3. Скільки діаметрів можна провести через точку, взяту:

а) на поверхні кулі;

б) всередині кулі?

Взаємне розміщення площини і кулі (сфери) в просторі

Як можуть розміщуватися в просторі куля (сфера) і площина? Нехай відстань від центра кулі (сфери) до площини дорівнює d, а радіус кулі (сфери) дорівнює r. Можливі три випадки (рис. 136).

1. Якщо d > r, то площина і куля (сфера) не мають спільних точок (рис. 136, а).

2. Якщо d < r, то площина і куля (сфера) перетинаються по кругу (колу) радіуса

О₁А = r² −d² (рис. 136, б).

3. Якщо d = r, то площина і куля (сфера) мають тільки одну спільну точку (рис. 136, в).

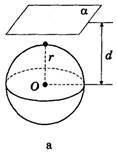
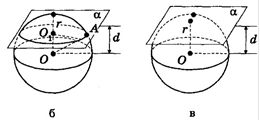
Рис. 136

Розв'язування задач

1. Кулю радіуса 5 см перетнуто площиною на відстані 3 см від центра. Знайдіть площу перерізу. (Відповідь. 16π см².)

2. Кулю перетнуто площиною на відстані 6 см від центра. Площа перерізу дорівнює 64π см². Знайдіть радіус кулі. (Відповідь. 10 см.)

3. Кулю перетнули площиною на відстані а від центра. Площа перерізу

Q ² дорівнює Q. Знайдіть радіус кулі. (Відповідь. +a .)



4. Кулю радіуса 41 см перетнули площиною. Площа перерізу дорівнює 1600π см². На якій відстані від центра кулі проведено площину? (Відповідь. 9 см.)

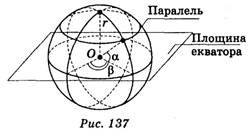Розв'язуючи задачі з використанням географічних координат, слід нагадати учням, що таке екватор, широта α і довгота β точки на поверхні Землі, що називається паралеллю (рис. 137).