Об'єм прямокутного паралелепіпеда

Про матеріал

Збірка задач прикладного змісту з теми "Об'єм прямокутного паралелепіпеда" у 5 класі

Перегляд файлу

Розв’язування задач прикладного змісту

на уроках математики.

Торак Наталія Володимирівна

учитель хімії та математики

Приморської філії

ОЗ «Академічний ліцей»

Скадовської міської ради

Херсонської області

учитель І категорії

Метою освіти сьогодення є не просто сума «знань, умінь, навичок» учня, а саме сформованість його особистісних, соціальних, пізнавальних та комунікативних здібностей. Завданням школи є забезпечення формування регулятивних навчальних дій учнів, орієнтованих на вміння визначати конкретну мету, прогнозувати ситуації та їх вирішення, коректувати, в разі необхідності, свої результати. Такі вміння ефективно формуються засобами змісту предмету «Математика». Одним із основних компонентів змісту вивчення математики в школі є задачі.

Для того, щоб забезпечити усвідомлене оволодіння учнями виділеними вміннями необхідно збагачувати зміст навчання математики завданнями, при вирішенні яких розкривається практико-орієнтований потенціал математичних знань і умінь. У зв'язку з цим, доцільно, включати в зміст навчання математики прикладні задачі.

Саме задачі виконують роль «містка» між теорією та практикою, наукою та повсякденним життям. Задачі прикладного характеру спонукають до розвитку логічного мислення в учнів, формування пізнавального інтересу до предмета, а також розкриття творчого потенціалу школярів. Прикладні задачі повинні відповідати певним вимогам: доступність матеріалу, пізнавальна цінність, використання реальних величин, ситуацій. Такі задачі виконують три основні функції:

Навчальну. Під час розв’язування задач відбувається пізнавальний процес; учні застосовують нові теоретичні знання; узагальнюють вивчений матеріал; знайомляться з новими методами розв’язування задач.
Розвиваючу. Під час розв’язування задач в учнів виробляється математичний стиль мислення. Це вміння використовувати формально логічну схему судження, це лаконічність письмового та усного викладення, чітка послідовність ходу мислення.
Виховну. Задача виховує в першу чергу своїм змістом. Виховне значення має й сам процес навчання розв’язуванню математичних задач. Методично грамотна постановка такого навчання виховує в учнів працелюбність, наполегливість.

Розв’язування задач прикладного характеру забезпечує розвиток умінь, самоорганізації, розвиває навички побудови алгоритму. Все це необхідне не тільки в рамках шкільного курсу, але й в реальних життєвих ситуаціях. На прикладі добре складених задач прикладного змісту учні переконуються у важливому значенні математики для багатьох сфер людської діяльності, її користі та необхідності для практичної роботи, усвідомлюють широту можливих застосувань математики, розуміють її роль в сучасній культурі.

Розв’язування прикладних задач результативне тоді, коли учні зустрічались з описуваними ситуаціями в реальному житті: в побуті, на екскурсії, під час вивчення інших предметів. Ефективним засобом є широке використання наочності: фото. Слайдів, плакатів, малюнків, кластерів, відео.

Пропоную збірку задач прикладного характеру з теми «Об’єм прямокутного паралелепіпеда» курсу математики 5 класу.

МАТЕМАТИКА НАВКОЛО НАС

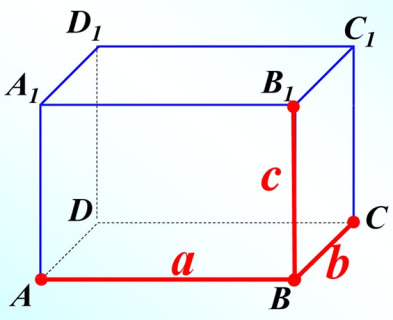
Об’єм прямокутного паралелепіпеда

5 клас

На заводі «Sandora» сік розливають в пакети по 1000 см³. Чи підійде для розливу пакет, що має розміри 6 см, 9 см, 20 см?

$C:\Users\юрий\Downloads\sandora_4823063106269_images_7500169296.jpg$

Розв’язок: V = a · b · c

6 см · 9 см · 20 см = 1080 см³

1080 см³ > 1000 см³, отже такий пакет підійде для розливу соку.

Класна кімната є основним місцем перебування учнів у школі, тому гігієнічному стану цих приміщень приділяється особлива увага. Недотримання «Санітарних норм» повітряного режиму погіршує сприйняття і засвоєння навчального матеріалу. Найменша кубатура повітря, що припадає на одного школяра сягає 4 м³. Скільки учнів можна розмістити у нашому класі, що має такі розміри: довжина - 8 м, ширина - 6 м, висота - 3 м.

$C:\Users\юрий\Downloads\unnamed (8).jpg$

Розв’язок: V = a · b · c

V = 8 м· 6 м ·3 м = 144 м³ – об’єм класної кімнати

144 м³ : 4 м³ = 36 учнів

Зелені насадження – «легені планети» тому, що виробляють, необхідний для дихання людини, кисень. Обчисліть скільки метрів кубічних повітря очистять від автомобільних газів 30 каштанів, посаджених уздовж дороги, якщо одне дерево очищує зону довжиною 100 м, шириною 12 м, висотою 15 м?

$C:\Users\юрий\Downloads\97136623_2937679079662022_1096852781026770944_o-1.jpg$

Розв’язок: V = a · b · c

V = 100 м· 12 м ·15 м = 18000 м³ – об’єм повітря, що очищує 1 дерево

18000 м³ · 30 = 540000 м³ - об’єм повітря, що очищує 30 дерев.

Сім’я має акваріум форми прямокутного паралелепіпеда , шириною 60 см і довжиною –

30 см, у який влито 6 відер води по 12 л у кожному. Яка глибина налитої води?

$C:\Users\юрий\Downloads\aquarium_PNG29.png$

Розв’язок: V = a · b · c с - ? с = V : (a · b)

12 л · 6 = 72 л = 72 дм³ = 72000 см³ – об’єм води

72000 см³: (60 см ·30 см) = 72000 см³ : 1800 см² = 40 см – глибина налитої води

Дитячий басейн має такі розміри: довжина - 15 м, ширина – 6 м, глибина – 1 м. Обчисліть об’єм басейну та об’єм води потрібний для його наповнення, маючи на увазі, що вода не має доходити до краю басейну на 30см.

$C:\Users\юрий\Downloads\basseyn-safari-1.jpg$

Розв’язок: V = a · b · c

100 см – 30 см = 70 см – висота води у басейні

1500 см · 600 см · 70 см = 63000000 см³ = 63000 дм³ = 63 м³ – об’єм води у басейні.

Сінник у дідуся має форму прямокутного паралелепіпеда з розмірами: довжина – 10 м, ширина – 5 м, висота 4 м. Знайдіть масу сіна в сараї, якщо маса 10 м³ сіна дорівнює 6 ц.

$C:\Users\юрий\Downloads\depositphotos_9171431-stock-photo-storing-hay-balls-in-autumn.jpg$

Розв’язок: V = a · b · c

12 м · 5 м · 4 м = 240 м³ – об’єм сінника

240 м³ : 10 м³ · 6 ц = 144 ц – маса сіна

На дитячому майданчику спорудили пісочницю з розмірами: довжина - 170 см, ширина - 150 см, глибина 30 см. Яку масу піску треба насипати у пісочницю, щоб шар піску був висотою на 10 см менше глибини пісочниці. (1 см³ піску має масу 2 г).

$C:\Users\юрий\Downloads\1-1-800x800-0.jpg$

Розв’язок: V = a · b · c

30 см – 10 см = 20 см – висота шару піску

170 см · 150 см · 20 см = 510000 см³ – об’єм шару піску

510000 см³ ·2 = 1020000 г = 1020 кг = 1 т 20 кг – маса піску.

На будівництво завезли цеглу і склали її на зберігання у формі куба, ребро якого дорівнює 120 см. Одна цеглина має розміри 30см, 10 см і 5 см. Скільки цегли завезли?

$C:\Users\юрий\Downloads\unnamed (9).jpg$

Розв’язок: V = a · b · c

120 см · 120 см · 120 см = 1728000 см³ – об’єм куба

30 см · 10 см · 5 см = 1500 см³ – об’єм однієї цеглини

1728000 см³ : 1500 см³ = 1152 – цеглини0 завезли на будівництво

Екскаватор повинен вирити траншею довжиною 54 м, шириною 2 м , глибиною 3 м. Який об’єм ґрунту доведеться вийняти екскаватору? Скільки разів доведеться зачерпнути ковшем грунт, якщо об’єм ківша 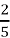м³?

$C:\Users\юрий\Downloads\unnamed (10).jpg$

Розв’язок: V = a · b · c

54 м · 2 м · 3м = 324 м³ – об’єм ґрунту

324 м³ : 2 · 5 м³ = 810 разів треба екскаватору зачерпнути ковшем.

На площі міста встановили однакові бетонні ємності для квітів, виготовлені у формі прямокутних паралелепіпедів, виміри яких дорівнюють: довжина - 40 см, ширина - 40 см і висота - 50 см. Товщина кожної з чотирьох бічних стінок становить 5 см, а товщина днища 10 см. Який об’єм бетону було використано для виготовлення 22 таких ємностей?

$C:\Users\юрий\Downloads\fa17b9cb3a5091ebca2af7b919j6--tsvety-i-floristika-kashpo-napolnoe-cube-15-sm-iz-betona.jpg$

Розв’язок: V = a · b · c

40 см · 50 см · 5 см = 10000 см³ = 10 дм³ – об’єм однієї бічної стінки

10 дм³ · 4 = 40 дм³ – об’єм чотирьох бічних стінок

40 см ·40 см · 10 см = 16000 см³ = 16 дм³ – об’єм днища

40 дм³ + 16 дм³ = 56 дм³ – об’єм бетону, необхідний для виготовлення однієї ємності

56 дм³ ·22 = 1232 дм³ – об’єм бетону, необхідний для виготовлення 22 ємностей.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Торак Наталія Володимирівна

Пов’язані теми

Математика, Матеріали до уроків

Додано

1 листопада 2021

Переглядів

5764

Оцінка розробки

Відгуки відсутні