«ОБ’ЄМИ ТІЛ ОБЕРТАННЯ, РОЗВ’ЯЗАННЯ ЗАДАЧ» РОЗРОБКА ІНТЕГРОВАНОГО УРОКУ ДЛЯ 11 КЛАСУ

РОЗРОБКА ІНТЕГРОВАНОГО УРОКУ З ГЕОМЕТРІЇ ДЛЯ 11 КЛАСУ

УЧИТЕЛЬ НВК «ГІМНАЗІЯ-ШКОЛА» № 27

ГУБСЬКА ОЛЕНА ФЕДОРІВНА

Тема уроку: «ОБ’ЄМИ ТІЛ ОБЕРТАННЯ, РОЗВ’ЯЗАННЯ ЗАДАЧ»

Мета уроку:

а) формування математичних, функціональних компетентностей учнів, вміння вчитися, аналізувати, робити висновки, застосовувати знання в нестандартних ситуаціях;

б) навчальна:

• актуалізація вже набутих раніше знань, вироблення умінь і навичок щодо застосування цих знань на практиці, закріплення матеріалу по розв’язанню задач на обчислення об’ємів тіл обертання, використовуючи задачі прикладного характеру та завдань для підготовки до ЗНО;
• розширення пізнавальних можливостей учнів, ознайомлення з теоремою Гульдіна для раціонального обчислення об’ємів деяких тіл обертання, які утворюються обертанням плоскої фігури навколо осі, яка лежить в площині цієї фігури та не перетинає її;
• формування вмінь та навичок виконувати вправи з переносом знань в нові умови, застосовувати знання англійської мови при розв’язанні геометричних задач на обчислення об’ємів утворених тіл;

в) розвивальна:

• визначення учнями межи можливостей застосування набутих знань;
• створення порівняльної характеристики різних способів розв’язання задачі, визначення зручності застосування деяких фактів геометрії;
• розвиток навичок працювати за зразком з метою вироблення безпомилкового застосування набутих знань;
• розвиток критичного мислення при проведенні дебатів, створенні кейсу завдань для домашнього завдання групи;

г) виховна:

• формування і розвиток навичок працювати в команді;
• формування соціальної компетентності.

Тип уроку: інтерактивний, комбінований.

Методи проведення уроку:

• метод «мозкового штурму» при розв’язанні тестових завдань ЗНО та повторенні основних фактів геометрії;
• «навчаючи - вчуся»;
• «круглий стіл»;
• дискусія;
• ситуаційний аналіз.

Інтерактивні застосовані технології:

• перевернутого навчання;
• колективно-групового навчання;
• опрацювання дискусійних питань;
• застосування ІКТ при розв’язанні задач;
• ситуативного моделювання;
• відкритого зворотнього зв’язку.

Форми проведення уроку:

• самостійна робота учнів;
• дебати;
• порівняльний аналіз методів розв'язання задач.

Обладнання:

• презентація для систематизації набутих раніше знань, усного розв’язання задач;
• картки з запропонованим українсько-англійським словником математичної термінології;
• картки з розміщенням центру мас в деяких геометричних фігурах для вивчення допоміжного матеріалу;
• картки із запропонованою схемою-підказкою розв’язування задач для учнів третьої групи з середнім рівнем навчальних здібностей.

ХІД УРОКУ:

  І. Організаційний момент. Привітання. Мотивація. Представлення теми, очікуваних результатів. (2 хв.)             

 1.1. Вчитель. Доброго дня, шановні учні! На попередньому уроці ми з вами розглядали розв’язування геометричних задач на обчислення об’ємів тіл обертання: циліндра, конуса, зрізаного конуса, кулі та їх частин. Сьогодні ми з вами продовжимо знайомитися з новими фактами, що можуть знадобитися для зручного обчислення об’ємів тіл обертання, зробимо висновки, чи потрібно це нам для розглядання. Вдома ви ознайомились з теоремою Гульдіна і українсько-англійським міні-словником. Подумайте, як це може бути задіяним в роботі?

 1.2. Вчитель застосовує презентацію, звертаючи увагу учнів на застосування тіл обертанні в різних сферах реального життя: фізики, хімії, природі, будівництві, різних механічних приладах, тому розглядання теми обчислення об'ємів тіл обертання є актуальним (додаток 1).

 ІІ. Етап перевірки якості виконання домашнього завдання, рівня підготовленості учнів. (10 хв.)

 2.1. Вчитель. Зараз пригадаємо матеріал, який ви розглядали на попередньому уроці, цим самим ми перевіримо якість виконання попереднього домашнього завдання і розв’яжемо деякі задачі усно для закріплення матеріалу. У вигляді методу «мозковий штурм» попрацюємо усно.

 Вчитель в довільній формі задає учням будь-які питання на знання теоретичного матеріалу, на питання необхідно відповідати дуже швидко, підтримувати бесіду. До оцінювання учнів буде враховано їх активність та вміння орієнтуватися в теоретичному матеріалі.

 Питання:

• властивість медіани в прямокутному трикутнику, яка проведена до гіпотенузи;
• формула для визначення площі сектора;
• теорема косинусів;
• метричні співвідношення в прямокутному трикутнику;
• довжина дуги кола;
• коли в опуклий чотирикутник можна вписати коло;
• властивість бісектриси трикутника;
• ознака перпендикулярності прямої і площини;
• теорема про три перпендикуляри;
• теорема синусів;
• формули площ многокутників та інші.

 2.2. Застосування презентації, повторення основних формул для обчислення об’ємів (додаток 2).

 2.3. Для перевірки якості виконання домашнього завдання учням пропонується виконати тестові завдання, які наближені до домашньої роботи і завдань ЗНО з даної теми (слайд № 8 - 13). Розв’язання кожної задачі, на яке відведено 1 хв., одразу проговорюється, перевіряється відповідь (додаток 3). В зошиті учневі не потрібно наводити повне рішення завдання, необхідно тільки показати план рішення, деякі обчислення і вказати отриману відповідь. Кожний учень критично ставиться до свого розв’язання, оцінює сам правильність своєї роботи при перевірці. При оцінювання роботи учнів учитель буде звертати увагу на вміння розв’язувати задачі та на об’єктивність свого оцінювання учнями. За кожну з розв’язаних правильно задач учень може отримати 0,5 бали.

Задача №  1.  Прямокутник зі сторонами і b ( > b ) обертається навколо більшої сторони. Визначити об’єм тіла обертання. Відповідь: . (В)

Задача №  2.

Знайдіть об’єм тіла, утвореного обертанням рівнобедреного прямокутного трикутника з гіпотенузою см навколо одного з катетів.

Відповідь: . (А)

Задача №  3.  У циліндр вписано куб, об’єм якого дорівнює . Визначити об’єм циліндра. Відповідь: . (Б)

Задача №  4.  Точка М, яка не належить площині, рівновіддалена від всіх вершин квадрата КСВР. МО - перпендикуляр до площини (КСВ). Вказати кут похилу площини (РМВ) до площини квадрата КСВР. Відповідь: .

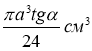Задача №  5.  Сторона основи правильної чотирикутної піраміди дорівнює . Бічна грань утворює з площиною основи кут . Визначити об’єм конуса, вписаного в піраміду. Відповідь: . (Д)

Задача №  6. Площа великого круга дорівнює . Знайти об’єм кулі.

Відповідь: . (Г)

 ІІI. Самостійна робота учнів, виконання тестових завдань ЗНО на обчислення об’ємів тіл обертання, обернений зв’язок. (8 хв.)

 Учням надано картки з тестами для самостійної роботи. Кожний учень отримає свою картку, на якій вказано номер варіанту. При оформленні роботи на аркуші учневі необхідно вказати правильну відповідь, наводити повне рішення не потрібно. Завдання самостійної роботи надано в додатку 4.

 ІV. Етап актуалізації суб'єктивного досвіду учнів, інтерактивні вправи. (15 хв.)

 3.1. Вчитель. В сучасному житті деякі ВНЗ практикують викладання математики англійською мовою (Київ, Харків), тому спілкування у поєднанні англійської мови та мови геометрії дозволить деяким із вас швидко адаптуватися до ВНЗ, з іншого боку це дає можливість не тільки закріплювати знання математики, а й готуватися до ЗНО з англійської мови.

3.2. Вчитель математики повідомляє учням про поставлену задачу англійською мовою, що надано у додатку 5.

 Вчитель. Вам необхідно виконати наступну роботу:

1. розв’язати задачу англійською мовою, застосовуючи наданий вам українсько-англійський словник необхідних математичних термінів (додаток 5);
2. пояснити рішення задачі англійською мовою при перевірці.

Потім це рішення буде надано вам на українській мові.

Мета завдання: формування навичок розуміти і розв’язувати математичні задачі, працювати в білінгвізмі.

Задача №  7. Рівнобічна трапеція з основами 5 см і 11 см обертається навколо більшої основи. Знайдіть об’єм тіла обертання, якщо висота трапеції дорівнює 4 см.

           Відповідь: .

 Для того, щоб учні адаптувалися до розгляду математичних задач англійською мовою, було обрано учнів-консультантів, які задають питання однокласникам на англійській мові, застосовуючи метод «навчаючи - вчуся» і технологію опрацювання дискусійних питань.

 3.3. Питання консультантів до учнів на англійській мові надано у додатку 6:

• Яке тіло утворюється при обертанні рівнобічної трапеції навколо більшої основи?
• Чи буде відрізнятися рішення і відповіді, якщо обертати трапецію навколо меншої основи, бічної сторони, будь-якої висоти трапеції?
• З об’ємів яких фігур буде утворюватися об’єм всієї фігури обертання?
• Чому дорівнює радіус основи і висота конуса, який є складовою тіла обертання?
• Чому дорівнює радіус основи і висота циліндра, який є складовою тіла обертання?

 Під час дискусії учнями було поставлене проблемне питання: чи будуть різними об’єми утворених тіл обертання, якщо обертати трапецію навколо більшої і навколо меншої основ? Для з’ясування вірної відповіді на це питання, учням було запропоновано обчислити об’єм тіл обертання в двох випадках, розв’язуючи задачу № 8 (слайд 16).

Задача №  8. Рівнобічна трапеція з основами 5 см і 11 см обертається навколо меншої основи. Знайдіть об’єм тіла обертання, якщо висота трапеції дорівнює 4 см.

           Відповідь: .

Об’єми виявилися різними, на що була звернена увага учнів при обговоренні рішень українською мовою.

  3.4. Наступна задача № 9 (слайд № 17) англійською мовою надана в додатку 6.

Задача №  9. Правильний трикутник із стороною 4 см обертається навколо

прямої, яка проходить через вершину трикутника паралельно протилежній стороні. Знайти об’єм тіла обертання.  Відповідь: .

Після розглядання рішень задач англійською мовою було проведено коректування рішень вчителем на українській мові.             

 Вчитель. Отже, перейдемо до наступного етапу нашого уроку, який будемо проводити українською мовою.

 V. Етап вивчення нових знань і способів діяльності, закріплення розглянутого матеріалу на практиці, представлення очікуваних результатів. (15 хв.)

Учням було надано домашнім завданням ознайомитися з теоремою Гульдіна. Вчитель. Давайте розглянемо розв’язання задачі № 8 іншим способом за теоремою Гульдіна. Об’єм тіла обертання, яке утворюється при обертанні будь-якої плоскої фігури навколо прямої, яка буде лежати в площині цієї фігури, але не перетинати її, можна обчислити за формулою , де - площа плоскої фігури, - відстань від центра мас фігури до прямої, навколо якої відбувається обертання. Вам надано картку (додаток 7), в якій показано особливості розміщення центру мас різних плоских фігур. Отже в трикутнику центр мас - точка перетину медіан трикутника і , , (слайд № 18).

Відповідь: .

 Розв’язання задач (додаток 8):

Задача №  10 (слайд № 19). Знайдіть об’єм тіла обертання, яке утворюється обертанням рівнобедреного трикутника з основою 12 см та висотою 15 см навколо його основи.

Рішення. , , .

Задача №  11 (слайд № 20). Знайдіть об’єм тіла обертання, яке утворюється обертанням ромба із стороною 14 см і гострим кутом навколо осі, яка проходить через вершину гострого кута паралельно його діагоналі. 

Рішення. , , .

Задача №  12 (слайд № 21). Знайдіть об’єм тіла обертання, яке утворюється обертанням рівнобедреного трикутника із бічною стороною 16 см і гострим кутом при вершині, навколо осі, яка містить бічну сторону трикутника. 

Рішення. ;  ; ; .

Задача №  13. Прикладна задача (слайд № 22). Чи можна зі шматка металу масою 44 кг виплавити деталь, яка утворена обертанням паралелограма зі сторонами 12 см, 7 см, гострим кутом  градусів навколо прямої, що паралельна меншій стороні паралелограма і розміщена на відстані 2 см від цієї сторони. Щільність металу 7,8 г /.

Вчитель. Вам необхідно відповісти на наступні питання, що дозволить сконструювати розв’язання задачі.

Питання:

• Яке тіло обертання утворює паралелограм при обертанні, з якими простішими тілами можна пов’язати утворене тіло обертання?
• Як обчислити масу тіла, що для цього необхідно знати, чи вистачає всіх даних для розв’язання задачі?
• Чому дорівнює відстань 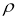в цій задачі?
• Як знайти 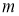для паралелограма?
• Як знайти висоту паралелограма?
• Як знайти площу паралелограма через сторони?

Розв’язання прикладної задачі:

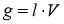• , де 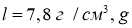- маса тіла обертання;
• ; ;
• ;
• ;
• ;
• .

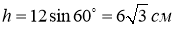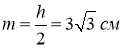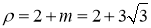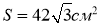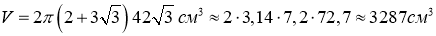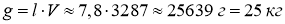Відповідь: із шматка металу можна виплавити деталь.

 VІ. Етап порівняльного аналізу. (10 хв.)

 Учням необхідно зробити порівняльний аналіз двох методів розв’язання задач на обчислення об’єму тіла обертання. В цій роботі учні повинні за допомогою дискусії, колективного обговорення скласти порівняльну таблицю переваг звичайного методу розбивки тіла на простіші тіла і методу застосування теореми Гульдіна. Учні працюють в групах, критично ставляться до підведення підсумків порівняння. На дошці учнями створюється порівняльна таблиця, яка надана в додатку 9.             

 VІІ. Інтерактивні вправи, практична частина. (15 хв. + 10 хв.)

7.1. Наступним етапом є використання частково форми та правил проведення інтелектуального математичного турніру. Всіх учнів розбито на три групи, які повинні 15 хв. самостійно виконувати  описані нижче завдання і захищати свої роботи по 2 хвилини. Виступ опонентів по 1 хв., рецензента 1 хв. Кожний учень першої групи повинен розв’язати дві задачі, одна з яких надана з підказками. За це завдання можна отримати два бали. Після виконання завдання командою вибирається доповідач, який пояснює рішення двох задач. Друга група в цей момент грає роль опонента, критично ставиться до доповіді першої групи. Третя група грає роль рецензента. Умови задач для першої і другої групи надано в додатку 10.

 7.2. Друга група учнів отримує від вчителя для самостійної роботи три задачі. За цю роботу учні можуть отримати три бали. Після виконання роботи групою обирається доповідач, який розповідає розв’язання цих задач. Третя група на цьому етапі грає роль опонента.

 7.3. Кожний учень третьої групи повинен виконати творче завдання: скласти свої дві задачі на застосування теореми Гульдіна і розв’язати їх. Це завдання для третьої групи оцінюється в чотири бали залежно від складності задачі. До кожної задачі необхідно створити інструкцію, яка допоможе іншим учням розв’язати ці задачі. Вони потрапляють до кейсу завдань, які будуть надані учням в наступних домашніх завданнях. Після виконання завдання групою обирається одна задача, яка буде зачитана під час захисту своєї роботи (додаток 11).

VІІІ. Рефлексія. Підведення підсумків роботи. Надання домашнього завдання. (5 хв.)

 8.1. Домашнє завдання: за підручником п. 35, № 1379, № 1380; № 1388.

 8.2. Підведення підсумків роботи на уроці. До оцінювання учнів входить:

• тестові завдання задач з перевіркою - 3 бали;
• самостійне розв’язання тестових задач  - 5 балів;
• самостійна робота по групах - 2, 3, 4 бали

8.3. Виступ учнів про важливість вивченого матеріалу, рефлексія, критичне оцінювання якості своєї роботи.