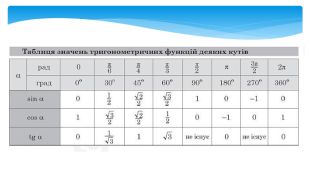
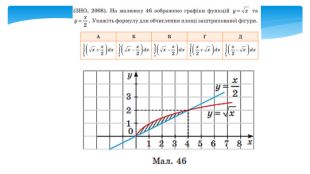
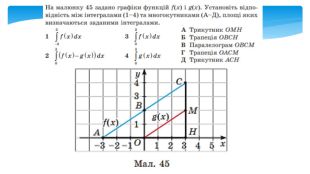
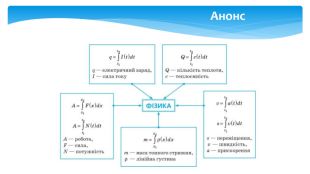
Обчислення площ плоских фігур
Про матеріал
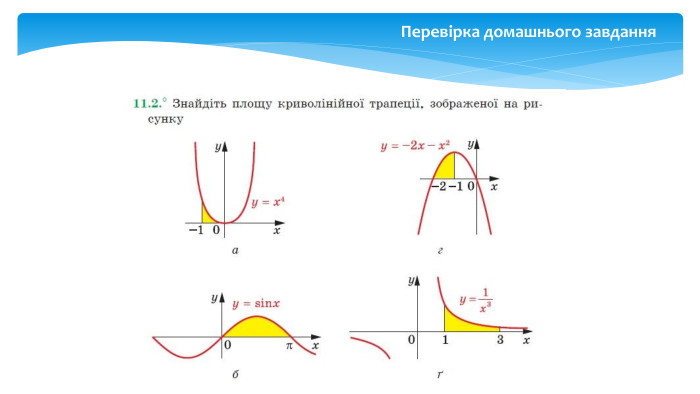
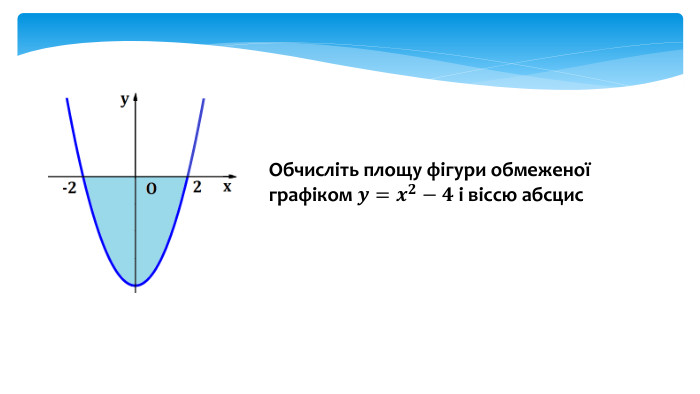
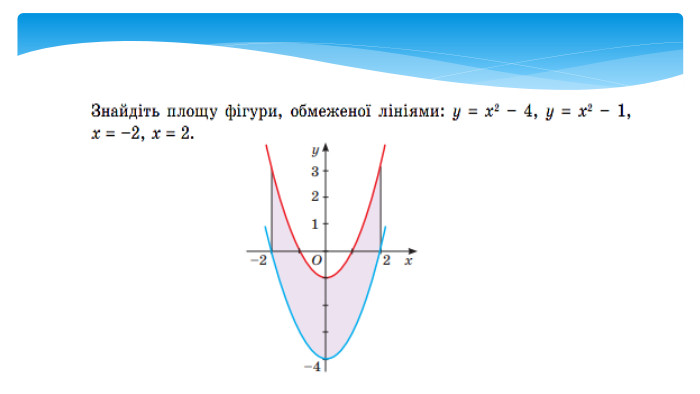
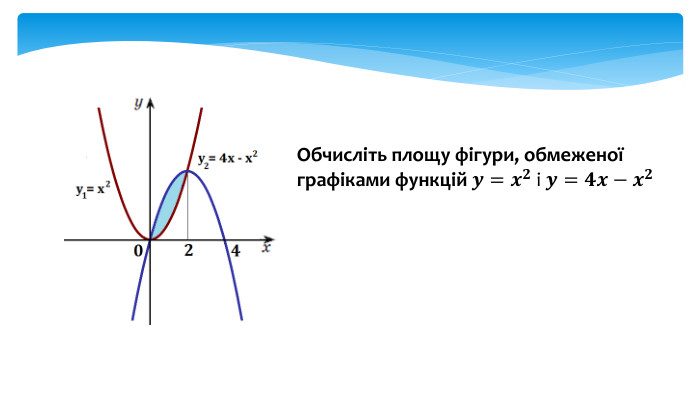
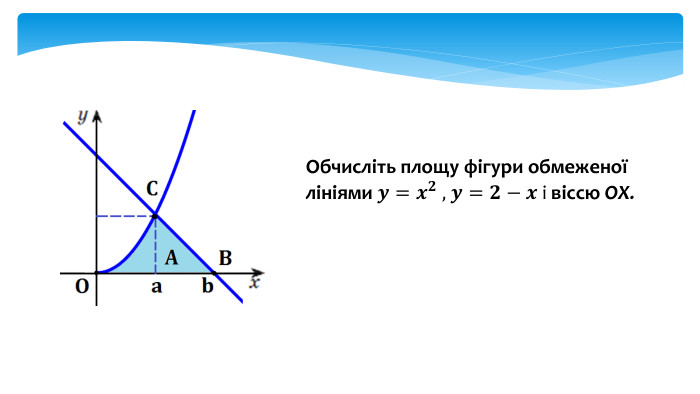
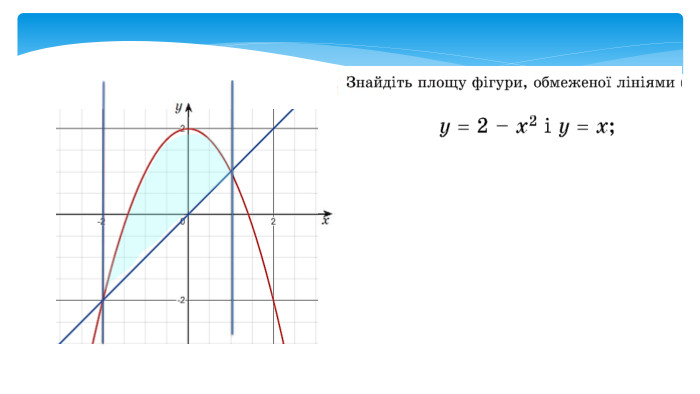
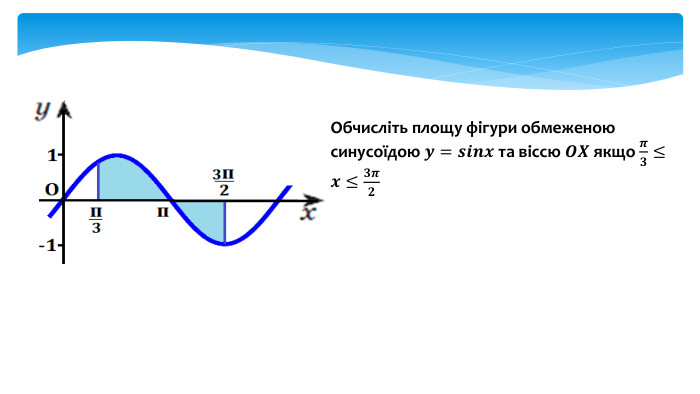
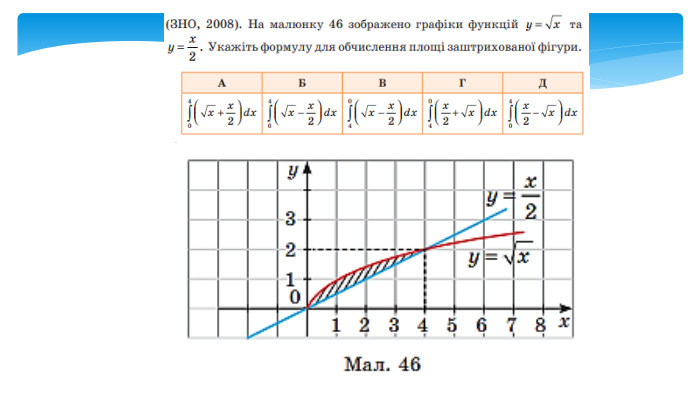
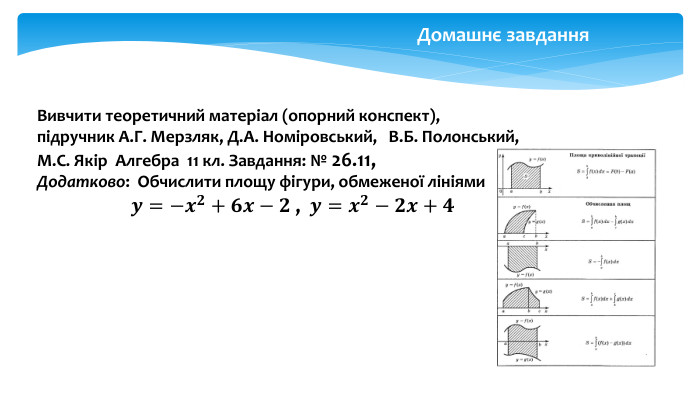
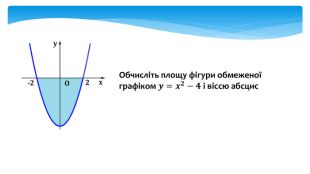
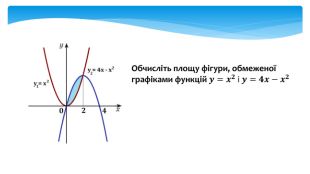
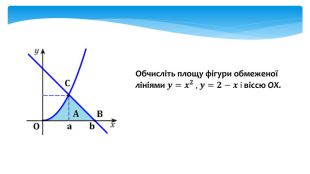
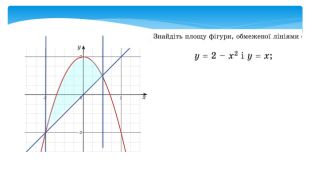
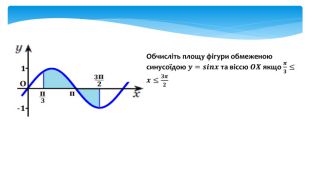
У даній презентації розглядається методика обчислення площ плоских геометричних фігур, що не є криволінийними трапеціями. Презентація містить візуальні приклади, що демонструють, як виглядають різні фігури та як їх площа змінюється в залежності від параметрів.Розв’язання практичних задач, які дозволяють учням закріпити отримані знання та навички. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку