Опис педагогічного досвіду вчителя математики

1. Автор досвіду: Дмитренко Марина Володимирівна, учитель математики Запорізького багатопрофільного ліцею  № 99 Запорізької міської ради Запорізької області

2. Базова модель досвіду

2.1 Тема досвіду: «Проблемний підхід до навчання математики як засіб активізації когнітивної діяльності  та розвиток креативних здібностей учнів».

2.2 Обґрунтування  актуальності та перспективності досвіду

Математика як навчальний предмет покликана передусім сприяти розумовому вихованню, особливо вихованню волі до цілеспрямованої розумової активності.

Отже, виховна функція навчального предмета «математика» має величезне значення в розвитку особистості і значно переважає пізнавальну функцію. Для кожного учня математика корисна, передусім, як полігон для тренування, як джерело проблем, які потрібно вирішувати. Тільки з постановки проблеми починається продуктивне мислення учня. Тому одним з найважливіших завдань математики є розвиток мислення здобувачів освіти, уміння робити висновки, тобто формування розумової культури, що характеризується певним рівнем розвитку критичного та логічного мислення, оволодіння загальними прийомами міркувань, бажанням набути знання і вміння, набути предметних та загальних компетентностей  та навчитися застосувати їх у життєвих ситуаціях. прддлшож

Особливо ефективним засобом активізації пізнавальної діяльності учнів є проблемний підхід до навчання математики, який сприяє інтелектуальному розвитку здобувачів освіти, залучає їх до пошуково-дослідницької роботи на уроках.

2.3 Теоретична основа досвіду.  Технології проблемного навчання не можна віднести до нових, його елементи зустрічалися в евристичних бесідах Сократа, а ґрунтовні дослідження розпочалися в середині минулого століття. Основні принципи проблемного навчання розроблялися С.Л. Рубінштейном, Д.Н. Богоявленським. Роботи ж Дж. Дьюї, П.Я. Гальперіна, Т.В. Кудрявцева, М.І. Махмутова, І.Я. Лернера та інших сприяли розкриттю проблеми інтелектуального розвитку, проблемного й розвивального навчання. У теорії М.І. Махмутова проблемним навчанням є «тип розвиваючого навчання, в якому поєднуються систематична самостійна пошукова діяльність учнів із засвоєнням ними готових висновків науки; система методів побудована з урахуванням цілі і принципу проблемності; процес взаємодії викладання і навчання орієнтований на формування пізнавальної самостійності учнів, стійкості мотивів навчання і розумових (включаючи і творчі) здібностей в ході засвоєння ними наукових понять і способів діяльності, детермінованого системою проблемних ситуацій» [4 с. 56]. Кудрявцев Т.В. дав таке визначення: «Проблемне навчання полягає у створенні перед учням проблемних ситуацій, в усвідомленні, прийнятті та вирішенні цих ситуацій учнями у ході спільної діяльності учнів з учителем при оптимальній самостійності перших і під загальним керівництвом останнього». [10, с.37].

Законодавчою базою є Закон України «Про  освіту»; Державний стандарт базової і середньої освіти,  Концепція «Нова українська школа».

2.4 Новизна досвіду полягає в орієнтації на наскрізні лінії навчання: «Підприємливість і фінансова грамотність», що забезпечить краще розуміння молодим поколінням українців практичних аспектів фінансових питань, уміння генерувати ідеї, ухвалювати оптимальні рішення, аргументувати та захищати свою позицію; «Екологічна безпека та сталий розвиток», що спрямована на формування в учнів соціальної активності, відповідальності та екологічної свідомості, готовності брати участь у вирішенні питань збереження довкілля і розвитку суспільства, усвідомлення важливості сталого розвитку для майбутніх поколінь; «Здоров’я та безпека», що забезпечить становлення учня як емоційно стійкого члена суспільства, здатного вести здоровий спосіб життя і формувати навколо себе безпечне життєве середовище; «Громадянська відповідальність», що сприятиме формуванню відповідального члена громади і суспільства, який розуміє принципи та механізми функціонування суспільства. На вищесказане безпосередньо впливає психологічний аспект проблемного навчання математики. пролоєд

2.5 Провідна педагогічна ідея досвіду. Концепція «Нової української школи» виділяє однією з ключових компетентностей – математичну компетентність. Це –  культура  логічного й алгоритмічного мислення: уміння застосовувати математичні (числові та геометричні) методи для вирішення прикладних завдань у різних сферах діяльності. Здатність до розуміння і використання простих математичних моделей. Уміння будувати такі моделі для вирішення проблем. Функція знання – уміння бачити проблему та будувати алгоритм її вирішення. Вважаю, що застосування проблемного навчання на уроках математики сприятиме розвитку продуктивного мислення учнів, критичного та логічного мислення, формуванню розумової культури, предметних та загальних компетентностей  та вміння застосувати їх у життєвих ситуаціях. Результатом такого навчання буде розвиток життєвих компетентностей учнів та підвищення якості навчання математики. ролдо

Тому  у своїй роботі я виділяю пріоритетним проблемний метод навчання.

3. Інформаційно-педагогічна модель досвіду

3.1 Мета: створення умов для формування конструктивної взаємодії  учасників освітнього процесу як умови творчого розвитку та саморозвитку кожного учня, формування математичної, фінансової, комунікаційної, громадянської, екологічної компетентностей, відчуття власного успіху, впевненості у власних творчих силах та власних судженнях. прод

3.2 Цілі:

– вирішити  проблему виявлення математично обдарованих учнів;

– сформувати в учнів компетенції відповідного рівня щодо роботи над вирішенням проблемних ситуацій;

– розробити стратегію та практику введення в роботу на уроці проблемних ситуацій та шляхів їх вирішення;

– створити оптимальні умови для учнів на уроці для використання проблемного навчання;

•                 розвинути в учнів вміння контролювати власний навчальний процес та вміння співпрацювати з іншими;

3.3. Завдання:

– удосконалення методичної бази дидактичними матеріалами для використання в роботі технології проблемного навчання; род

– активізація творчого потенціалу обдарованих учнів;

•                 розвиток розумових здібностей учня як суб’єкта навчання;
•                 підвищення мотивації навчально-пізнавальної діяльності; ролд
•                 виховання самостійності, активності та креативності, що сприяє всебічному розвитку особистості, здатної вирішувати життєві завдання;

–     реалізація компетентнісного підходу  до навчання: проектування вирішення проблемних математичних завдань на життєві проблемні ситуа ції.

3.4.  Тривалість роботи над темою досвіду

В межах впровадження моделі «Авторської школи» та роботи ПМК вчителів математики ЗБЛ № 99 над методичною темою «Формування інноваційного освітнього середовища на основі педагогіки співробітництва та реалізації компетентнісного підходу і принципу дитиноцентризма» працюю над темою «Проблемний підхід до навчання як засіб активізації когнітивної діяльності  та розвиток креативних здібностей учнів» з 2017 року.

4. Технології  реалізації  інноваційної розробки (досвіду)

У ліцеї над  розвитком продуктивного мислення в здобувачів освіти працюють постійно. А продуктивне мислення, як свідчать результати психологічних досліджень, невіддільне від роз’яснення тієї чи іншої проблеми. Даний вид мислення не тільки починається з постановки проблеми чи запитання, здивування чи непорозуміння, із суперечності, а й далі відбувається в процесі виникнення та розв’язання ряду послідовних пізнавальних завдань, проблем у цілому. Проблема – це завжди знання про незнання, тобто усвідомлення недостатності знань для задоволення певної  пізнавальної потреби. пролж

Усвідомлення проблеми відбувається в проблемній ситуації й залежить від рівня знань, спрямованості пізнавальних інтересів учня.

Те, що є проблемним для одного, може не бути проблемним для іншого учня. Кожна людина бачить тим більше нерозв’язаних проблем, чим ширше коло її знань. Уміння бачити проблему – функція знання. У такий спосіб проблемна ситуація характеризує певний психічний стан учня, що виникає під час виконання завдання й допомагає йому усвідомити суперечність між необхідністю виконання завдання й неможливістю здійснити це за допомогою наявних знань. Усвідомивши суперечність, учень відчуває потребу здобути нові знання про предмет, спосіб чи умови виконання дій. пр

Проблемне навчання спрямоване на засвоєння здобувачами освіти знань і способів діяльності шляхом сприйняття пояснень учителя в умовах проблемної ситуації, самостійного (або за допомогою вчителя) аналізу проблемних ситуацій, формулювання проблем і їх рішення за допомогою висунення пропозицій, гіпотез, їх обґрунтування і доведення, а також шляхом перевірки правильності рішення. Основними перевагами цього методу є розвиток розумових здібностей учня як суб’єкта навчання; підвищення мотивації навчально-пізнавальної діяльності; виховання самостійності, активності та креативності, що сприяє всебічному розвитку особистості, здатної вирішувати життєві завдання. пролж

Використовуючи методи проблемного навчання математики у своїй роботі, розумію,  що ця технологія не в змозі вирішити всіх проблем, що виникають під час освітнього процесу, але бачу її значні переваги в порівнянні з традиційним навчанням. Проведемо  порівняльну  характеристику традиційного і проблемного навчання математики.

Порівняльна характеристика традиційного та проблемного навчання

 

Поряд з перевагами не можна забувати й про недоліки цього методу. Таке навчання не принесе результатів, якщо учні не підготовлені до нього за своїм розвитком та рівнем знань. Воно вимагає високої кваліфікаційної підготовки вчителя та більше часу для підготовки та реалізації. рол

Проблемне навчання математики реалізується шляхом вирішення проблем або створення проблемних ситуацій.  Проблемою вважають різновид питання або цілий комплекс питань, відповідь на які не міститься в накопичених учнями знаннях і способах діяльності, тому потребує відповідних практичних дій, які не є простим інформаційним пошуком, а, значить,  становить практичний чи теоретичний інтерес. Таке питання має містити в собі деяке утруднення для учнів, передбачати можливість висування ними гіпотези та обов’язково   відображатися на емоціях школярів (подив, невдоволення наявними знаннями тощо). Проблема має вирізнятися доступністю, своєю природністю та зацікавлювати учнів. прожд

Проблемною ситуацією можна назвати спеціально організовану вчителем взаємодію школярів з предметом пізнання, яка дозволяє виявити інтелектуальне утруднення або пізнавальне протиріччя та спонукає до подальшого пошуку шляхів його розв’язання. Створення проблемних ситуацій в навчальному процесі підпорядковується певним дидактичним цілям.

 

 

 

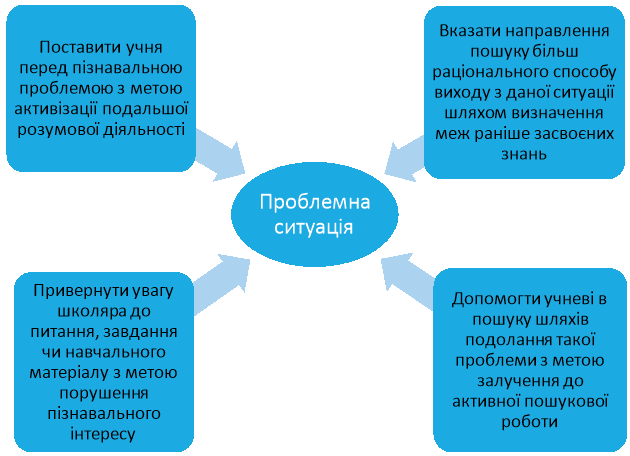
Від того, наскільки правильно поставлена проблемна ситуація, залежить не тільки ефективність, але й можливість подальшого проблемного навчання. про

Для того, щоб на уроках математики ефективно активізувати розумову діяльність учнів за допомогою проблемних ситуацій, у своїй роботі враховую  особливості проблемного підходу до навчання математики.  Застосування проблемного навчання на уроках математики має свої особливості: можна визначити основні типи проблемних ситуацій, способи їх створення, за яким планом здійснюється проблемне навчання і як відбувається підготовка до нього. прол

Підготовчий етап:

Насамперед учитель аналізує заздалегідь:

1. Якою має бути послідовність міркувань учнів, що призводить до розв’язування навчальної проблеми.
2. Чим вона зумовлена.
3. Коли ефективніше провести підготовчу роботу – до чи після постановки проблеми. олрд

Планування підготовчої роботи ґрунтується також на тому, що:

1. Наявність знань – вихідна позиція для сприйняття і усвідомлення нової інформації.
2. Майбутні знання використовуються в процесі мислення для розв’язування та формування навчальних проблем. ролж

Етапи процесу розв’язування навчальних проблем. Алгоритм роботи:

1. Актуалізація опорних знань, навичок, умінь шляхом цілеспрямованого повторення і роз’яснення підготовчих вправ на уроці.
2. Створення на уроці проблемної ситуації. Постановка теми уроку у вигляді навчальної проблеми. итьб
3. Осмислення, сприйняття здобувачами освіти навчальної проблеми.
4. Висунення гіпотези, здогадів про можливості розв’язання навчальної проблеми.
5. Експериментальне відтворення правильності запропонованої гіпотези.
6. Теоретичне обґрунтування гіпотези, узагальнення розв’язуваного твердження. прол
7. Закріплення усвідомленого матеріалу. Повторення і аналіз процесу розв’язання проблеми. Творче застосування здобутих знань для розв’язання практичних завдань.
8. Перевірка якості й глибини засвоєння учнями проблемного завдання, проведення короткочасних самостійних робіт. ролд

Звичайно, наведена схема не свідчить про те, що завжди існує чітке розмежування й суворе дотримання послідовності між перелічуваними етапами. Інколи ряд етапів виступає одночасно, інші можуть бути відсутні.

Наведу приблизну структуру проблемного уроку.

1. Актуалізація опорних знань 
   1.                   Активізація пізнавальної діяльності учнів. ролд

Мета: повторити попередній матеріал, пов’язаний з новою темою.

2.                   Повідомлення теми та мети уроку.

Мета: визначити тему та мету уроку.

3.                    Постановка головного проблемного питання уроку.

Мета: обрати основну проблему, яку вирішуватимуть учні на уроці.

2. Вивчення нового матеріалу
   1.                   Створення умов розгортання проблемної ситуації.

Мета: подати учням інформацію (або допомогти її відшукати), необхідну для розв’язання проблеми, залишивши місце в ній для роздумів.

2.                   Формулювання гіпотези. прол

Мета: висунути припущення щодо ймовірних шляхів подолання проблеми на основі наявних знань та отриманої інформації.

3.                    Організація навчальної діяльності щодо перевірки гіпотези.

Мета: довести або спростувати гіпотезу (в якості джерела допоміжної інформації може виступати підручник, посилання, довідник, відео).

4.                   Розв’язання головного проблемного питання уроку.

Мета: вирішити головне проблемне питання уроку шляхом обмірковування істинності гіпотези. прлд

3. Закріплення
   1.                   Аналіз результатів пошукової діяльності.

Мета: узагальнити та систематизувати основні етапи розумово-пошукової діяльності через усну та письмову форми роботи.

2.                   Закріплення нових знань і способів дій.

Мета: закріпити нові знання та способи дій, отримані в результаті вирішення проблемної ситуації уроку. прол

Безумовно, що кожен урок неможливо зробити проблемним, але системність у роботі необхідна. Можна використовувати елементи проблемного методу на різних етапах уроку. Якщо говорити про доцільність використання проблемного навчання, то, на мою думку, воно виправдане під час формування інтересу до вивчення конкретного матеріалу на етапі постановки мети та мотивації пізнавальної діяльності; в процесі оволодіння змістом навчання на етапі осмислення та засвоєння, наприклад, під час самостійної роботи або ж на етапі закріплення засвоєного у нових ситуаціях; для виявлення рівня засвоєння змісту освіти, активності та самостійності на етапі контрою навчально-пізнавальної діяльності учнів. прол

Приклади проблемних ситуацій для певного етапу уроку

Етап уроку	Тема уроку, клас	Проблемне завдання
Активізація пізнавальної діяльності	Порівняння десяткових дробів, 5 клас	1) Чи вірна нерівність: 12,5  12,413; 6,7  6,700? 2) Який знак потрібно поставити між 2 і 3, щоб одержане число було більше, ніж 2 і менше ніж 3?
	Середнє арифметичне, 5 клас	Задача: на уроці математики дівчата класу отримали оцінки: 7, 10, 12 та 8. Хлопці мали такі оцінки: 8, 11, 11, 10. Хто результативніше попрацював на уроці, хлопці чи дівчата?
	Відсоткове відношення, 6 клас	Задача: за підсумками семестрового оцінювання в 6-А класі з 28 учнів 7 відмінників, а у 6-Б класі з 32 учнів 8 відмінників. Який клас  лідирує у навчанні?
	Ознака подільності на 3 та 9, 6 клас	351 кратне 3, а 241 не кратне 3 672 кратне 3, а 802 не кратне 3 333 кратне 3, а 330 не кратне 3 Чому?
Вивчення нового матеріалу	Множення десяткових дробів, 5 клас	Порівняти відповіді й зробити припущення щодо множення десяткових дробів: 625×48=30000                6,25×4,8=30,000 126×78=9828                  12,6×7,8=98,28 858×32=27456                85,8×3,2=274,56.
	Додавання раціональних чисел, 6 клас	Виконати практичне завдання й висунути припущення щодо додавання чисел з різними знаками: 1) Зранку стовпчик термометра показував  8 С, до вечора температура підвищилася на 5 С. Якою вона стала надвечір? 2) Температура повітря вранці дорівнювала  3 С, а впродовж дня піднялася на 5 С. Якою вона стала надвечір?
	Множення звичайних дробів, 6 клас	Звичайні дроби перевести у десяткові та виконати множення, одержану відповідь представити у вигляді звичайного дробу та висунути припущення щодо множення звичайних дробів:
Засвоєння нових знань	Знаходження дробу від числа, 5 клас	Знайти утруднення при знаходженні дробу від числа та висунути припущення щодо його розв’язання: 0,5 від 124 1,2 від 14 0,75 від 48 20% від 65
	Розкладання натуральних чисел на прості множники, 6 клас	Знайти помилки в розкладі даних чисел на прості множники та пояснити, чому ці твердження не є вірними: 120 = 2×3×4×5 1539 = 9×19 7497 = 3×7×51
	Модуль числа, 6 клас	Записати числа, модулі яких дорівнюють числам: 4; 0,32; ½; 3 ¾.

 

Саме проблемність навчання стає внутрішнім мотиватором, що спонукає дітей шукати нові знання та нові способи діяльності, а в руках вчителя є потужним інструментом впливу на них. Виникає суперечність між потребою в нових знаннях і знаннями, які має учень, що сприяє активізації його пізнавальної діяльності та утримання стійкого інтересу до предмету вивчення. У такому разі пошук шляхів виходу з проблемної ситуації для школяра є основним механізмом розвитку його здібностей і вищих психологічних функцій взагалі. олдж

Пропоную наступні варіанти створення проблемних ситуацій на уроках математики.

1. Створення проблемних ситуацій через навмисне допущені вчителем помилки

У розумінні дітей вчитель – це комп'ютер, який не може помилитися  ніколи, і вони зазвичай сліпо копіюють його розв’язки. прлд

Приклад 1. Тема «Арифметичні дії з десятковими дробами», 5 клас.

Швидко розв’язую рівняння:

(х + 6,5) – 7,9 = 18,4

х + 6,5 = 18,4 – 7,9

х + 6,5 = 10,5

х = 10,5 – 6,5

х = 4.

Зрозуміло, що при перевірці відповідь не сходиться. Шукаючи помилку, діти вирішують проблему. Після цього учні ретельно стежать за думкою та розв’язками вчителя. Результат – уважність і зацікавленість під час уроку. олдж

Приклад 2. Даю завдання додому і кажу: "В мене не виходить. Спробуйте ви». Хоча завдання вирішується. На наступному уроці у більшості учнів радісні обличчя, бо вони впорались.

2. Створення проблемних ситуацій через використання цікавих завдань рол

Приклад 1. Тема «Коло. Круг», 6 клас.

Грають п’ятеро діток. Запрошую до дошки учня, на якій заготовлена таблиця. Учень з класу називає певне значення радіуса, учень біля дошки має знайти діаметр та довжину кола з таким радіусом, а також обчислити площу круга даного радіусу. Другий учень називає діаметр кола, учень біля дошки має обчислити радіус, довжину кола та площу круга. Третій учень називає довжину кола, а учень біля дошки знаходить його радіус, діаметр та площу круга. Четвертий називає площу круга. Діти класу стежать за розв’занням біля дошки, перевіряють можливі помилки. Виграє той учень, який заповнить таблицю без помилок. прол

Приклад 2. Тема «Степінь раціонального числа», 6 клас.

Злочинці викрали з банку велику суму грошей. Їх затримали, але викрадену суму встановити не вдалося. Злочинці категорично відмовляються назвати її, стверджуючи, що записали це число у вигляді степеня. Експертам вдалося дізнатися основу степеня. Це число 3, а саме число знаходиться в межах від 500 до 900. Але яким був показник не говорять. Даю час для піднесення числа 3 до необхідного степеню, щоб максимальна кількість учнів швидко отримала правильний результат (729).

3. Створення проблемних ситуацій через вирішення завдань, пов'язаних з життям

Приклад 1. Тема «Відсоткові розрахунки», 6 клас.

Групова гра «Бухгалтер магазину комп’ютерної техніки».

Стара ціна (в грн.)	Підвищення ціни		Нова ціна (в грн.)
	у відсотковому відношенні	в гривнях
8 000	5 %
11 000	10 %
20 000	15 %
45 000	20 %
32 000	25 %

Проблемна ситуація: потрібно удосконалити вміння підвищувати відсоток числа.

Приклад 2. Тема «Площа прямокутника», 5 клас.

Влітку необхідно пофарбувати підлогу в класі. Давайте з вами порахуємо, скільки потрібно грошей, якщо 1 банка фарби коштує 140 грн. Такої банки вистачить, щоб пофарбувати 35 кв. м. Для вирішення цієї задачі нам потрібно знайти площу підлоги (площа прямокутника). прл

4. Створення проблемних ситуацій через виконання практичних завдань

Приклад 1. Тема «Масштаб», 6 клас.

Виміряти за картою відстань між містами: Київ – Харьків; Київ – Вінниця; Київ – Запоріжжя; Київ – Одеса; Київ – Миколаїв. Знайти відстань між цими містами, якщо масштаб карти складає 1 : 10 000 000. Яке місто розташоване ближче до столиці? прол

Приклад 2. Тема «Ознаки подільності», 6 клас. ролд

Друзі-капітани в один день відбувають у рейс на різних пароплавах з тривалістю 18 діб і 12 діб. Через кілька діб друзі знову зустрінуться а порту?

5. Створення проблемних ситуацій через рішення задач на увагу і порівняння ролд

Приклад 1. Даші вчителька дала завдання порахувати, скільки трикутників зображено на малюнку. Вона знайшла 5 трикутників. Підійшла Маша та відшукала 7 трикутників. Хто з них правий? Спробуємо порахувати разом. Визначте, скільки трикутників ви бачите на малюнку та скільки чотирикутників? Що спільного в даних фігурах? Чим вони відрізняються?

Приклад 2. Тема «Скорочення дробів», 6 клас.

Відновити записи:

6. Створення проблемних ситуацій через різні способи вирішення однієї задачі

Приклад. Тема «Розв’язування задач за допомогою рівнянь», 5 клас.

На полиці стояли книги. Після того, як з полиці взяли 12 книг, а поставили – 9 книг, книг на полиці стало 39. Скільки книг стояло на полиці спочатку?

Розв’язують алгебраїчним способом:

(х – 12) + 9 = 39

х – 12 = 30

х = 42 (кн.)

А вчора четверокласник Стас, який не вміє розв’язувати такі рівняння, теж зміг розв’язати цю задачу. Проблемна ситуація: який спосіб він запропонував (арифметичний). олдж

7. Створення проблемних ситуацій через виконання невеликих дослідницьких завдань

Приклад. Тема «Довжина кола», 6 клас.

Ще стародавні греки знаходили довжину кола за формулою С = π·D, D – це діаметр кола. А що ж таке π?

Працюємо в парах, виконуючи необхідні вимірювання:

1. Обвити склянку ниткою, розпрямити нитку, довжина нитки приблизно дорівнює довжині кола склянки. Щоб отримати більш точний результат, потрібно це виконати кілька разів. Занесіть дані в таблицю.

2. Виміряйте діаметр склянки лінійкою. Дані занесіть у таблицю.

3. Знайдіть значення π як невідомого множника.

4. Кожній парі занести обчислене значення π в таблицю.

Висновок: значення π від 3,1 до 3,2 π це нескінченна дріб, сучасні машини можуть визначити до мільйона знаків після коми. π = 3,1415926... У подальшій роботі ми будемо використовувати значення π = 3,14.

Дослідження проведене. На уроці, крім дослідницької роботи, вдало використовувалася робота в парах. Співробітництво та взаємодопомога принесли бажаний результат. Дослідження допомагають розширити кругозір учня, підвищити самооцінку, самостверджуватися, формувати дослідницьку компетентність. длопа

Різноманітні проблемні ситуації не тільки допомагають активізувати розумову діяльність учнів, розвивати логічне мислення, пам’ять, увагу, а ще й підвищують інтерес до математики як науки. Для того, щоб зберегти дитячу зацікавленість та створити дійсно сучасний урок, зекономити час та зробити освітній процес якіснішим, неодмінно впроваджую проблемний метод за допомогою інформаційних технологій, а саме елементів дистанційного навчання для диференціації домашнього завдання. род

5. Результативність досвіду

Результати власної педагогічної діяльності свідчать про:

•                 очікуване підвищення мотивації навчально-пізнавальної діяльності в учнів;

•                 креативне застосування учнями знань, вмінь та навичок, отриманих на уроках математики, в практичній діяльності;
•                    опанування учнями математичних знань, вмінь та навичок різного рівня складності: від мінімальних, відповідних обов'язковим результатами навчання, до підвищених, що дозволяють продовжити навчання в класах з поглибленим вивченням математики; ролд
•                 наявний перехід від формального заучування правил та дій до пошуку знань через висування припущень, їх підтвердження або спростування;
•                 свідоме використання учнями навичок самоконтролю та взаємоконтролю.

У контексті оновлення освіти застосування проблемного навчання на уроках математики сприяє підготовці учнів до реалій життя, розвиває їх інтелектуальні та творчі здібності, мотивує опанування знаннями, яких вимагає сьогодення, сприяє розвитку вміння спілкуватися, співпрацювати з іншими людьми з метою вирішення спільних проблем, формує вміння здобувати та опрацьовувати інформацію, проявляти гнучкість у ході постійних змін у житті. ролд

Учні посідають призові місця на  олімпіадах (в тому числі в форматі онлайн), беруть активну участь у Міжнародному математичному конкурсі «Кенгуру», є постійними учасниками різноманітних шкільних та районних заходів.

Працюючи над даною темою, впроваджувала проблемне навчання продовж вивчення теми «Подільність натуральних чисел» в одному (6-А) з чотирьох класів, і за результатами семестрового  оцінювання, він значно випереджає решту.

 

Таблиця успішності учнів

за результатами річного оцінювання в 2018-19 н.р.

Клас	Кількість учнів	% якість знань
6-А	30	90 %
6-Б	32	62,5 %
6-В	31	64,5 %
6-Г	26	61,5 %

 

Таким чином, можна зробити висновок, що проблемний метод навчання математики досить ефективний, при систематичному застосуванні впливає на інтелектуальний розвиток здобувачів освіти, є важливим засобом пробудження в учнів активного мислення і ефективним стимулом для розвитку та зміцненню пізнавальних інтересів. ролд

6. Рекомендації щодо впровадження досвіду

Матеріали досвіду можуть  використовуватись шкільним методичним об’єднанням вчителів математики, шкільними творчими групами впровадження особистісно-орієнтованих технологій. ролд

7. Додатки

Додаток 1. Розробка уроку «Дільники та кратні натурального числа»

Додаток 2. Розробка уроку «Розкладання чисел на прості множники»

Додаток 3. Посилання на власні джерела

Додаток 4. Сертифікат про публікування авторського матеріалу