Урок з теми "Корінь n-го степеня. Арифметичний корінь n-го степеня та його властивості.




![]()
Тема. Корінь n-го степеня. Арифметичний корінь n-го степеня та його властивості.
Мета уроку: повторити й систематизувати значення учнів про поняття кореня n-го степеня й арифметичного кореня n-го степеня, сформувати знання про властивості кореня n-го степеня; формувати вміння застосовувати ці знання під час перетворення виразів. Формувати інформаційну та полікультурну компетентність. Сприяти формуванню та розвитку інтелектуальних та творчих здібностей учнів. Розвивати логічне мислення, математичну мову, пізнавальний інтерес учнів, вміння шукати цікаву інформацію. Виховувати відповідальність, прагнення до самовдосконалення, патріотизм, любов до рідного краю.
Компетенції: Спілкування державною мовою: розуміти, пояснювати і перетворювати тексти математичних задач (усно і письмово), грамотно висловлюватися рідною мовою; доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень; поповнювати свій словниковий запас
Тип уроку: засвоєння нових знань.
Обладнання: мультимедійний проектор, робочий зошит учня, підручники, комп'ютерна презентація, інтерактивні завдання розроблені в додатку Learning Apps
Структура уроку
І. Організаційний момент.
Перевірка готовності учнів до уроку, відмітка присутніх (відсутніх), налаштування на роботу. На партах для кожного учня приготовлені робочі зошити з друкованою основою.
ІІ. Мотивація навчальної діяльності
Я хочу розпочати наш урок із слів поета Миколи Дорізо: «Життя – як розв’язування задачі. З невдачі зумій ти добути корінь удачі». Отже, сьогодні ми будемо не тільки знаходити корінь n-го степеня, але й «добувати корінь удачі».
І удача сьогодні буде на стороні тих учнів , які використавши свої знання та вміння з вивченої теми.
В попередніх класах ви вивчили означення квадратного кореня, властивості, застосовували ці властивості до перетворення виразів з коренями. Та якщо існує дія піднесення до степеня ( квадрат, куб, четверта степінь числа ), то і існує обернена дія – добування кореня п –го степеня . Тому на сьогоднішньому уроці ми з вами розширимо поняття кореня n–го степеня і вивчимо його властивості.
III. Актуалізація опорних знань учнів
Давайте пригадаємо поняття, з якими нерозривно пов’язане вивчення даної теми.
- Дайте означення кореня n-го степеня.
-
Сформулюйте означення арифметичного кореня n-го степеня із числа
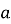 .
.
- Чи має зміст вираз -3
-
Обчисліть
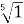
- Обчисліть значення корення n-го степеня з чисел.
https://learningapps.org/watch?v=pjz567onn19
IV. Пояснення нового матеріалу
Мета етапу:
• надати учням достатньо інформації для того, щоб на її основі вони могли виконати практичні завдання за мінімально короткий час;
• визначення учнями особистого розуміння отриманої інформації;
• пояснення змісту опрацьованого, порівняння реальних результатів з очікуваними.
Діяльність викладача:
Викладач пояснює основні властивості кореня n-го степеня та разом з учнями обговорює приклади на застосування даних властивостей.(Слайд №5-8)
- Корінь n-го степеня з добутку.
![]()
![]() Теорема . Корінь n-го степеня з добутку двох невід’ємних чисел дорівнює добутку коренів n-го степеня із цих чисел.
Теорема . Корінь n-го степеня з добутку двох невід’ємних чисел дорівнює добутку коренів n-го степеня із цих чисел.
Наприклад:1) ![]() 2)
2) ![]() =5
=5
- Корінь n-го степеня з дробу
![]()
 Теорема. Корінь n-го степеня з дробу, чисельник якого невід’ємний, знаменник додатний, дорівнює кореню n-го степеня із чисельника, поділеному на корінь n-го степеня із знаменника.
Теорема. Корінь n-го степеня з дробу, чисельник якого невід’ємний, знаменник додатний, дорівнює кореню n-го степеня із чисельника, поділеному на корінь n-го степеня із знаменника.
Наприклад: 1) ![]() 2)
2) ![]()
- Корінь n-го степеня із степеня
![]()

Наприклад:![]() 1)
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
- Корінь n-го степеня із кореня
![]()
![]()
Наприклад:![]() 1)
1)![]() ; 2)
; 2)![]() .
.
![]()
![]()
Наприклад:![]() 1)
1)![]() ; 2)
; 2)![]() .
.
Цікаво. Повідомлення учнів.
Радикал – це математичний знак, яким позначають дію вилучення кореня. На латинській мові “сторона”, “бік”, “корінь” позначаються одним і тим же словом radix. Математики античного світу, замість “добути корінь” говорили “знайти сторону, відповідно заданій площі квадрату”. Тому, раніше корінь квадратний називали “стороною”.
Від слова radix утворені терміни “радикал” і“корінь”, які ввійшли в математику завдяки Йоганну із Севільї (1140рік), Роберту Честерському (1145рік) і Герарду із Кремони (1150рік). Знак кореня ввів автор першого підручника з алгебри на німецькій мові, німецький математик Кристоф Рудольф (1525 рік). Він позначив корінь квадратний через √. Відбувається цей символ від стилізованої першої літери того ж слова radix.

V. Первинне закріплення нового матеріалу
Розв’язуємо гуртом.
№1 Знайти значення виразу:
![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]()

№2 Знайдіть значення виразу:
-
 ; 2)
; 2) 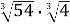 ; 3)
; 3) 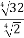 ; 4)
; 4) 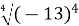 ;5)
;5) 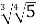 ;6)
;6)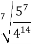

№3 Знайдіть значення виразу:
![]() .
.![]() ;
; ![]() .
.![]()

№4 Порівняйте числа.
-
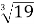 і
і 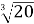 ; 2)
; 2) 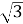 і
і 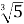

VI. Перевірка набутих умінь та навичок
![]() Готуємось до ЗНО
Готуємось до ЗНО
(2009) 3.Знайдіть значення виразу:
|
А |
Б |
В |
Г |
Д |
|
4 |
18 |
64 |
2 |
8 |
![]() (2014) 9. Обчисліть
(2014) 9. Обчисліть
|
А |
Б |
В |
Г |
Д |
|
-5 |
1 |
5 |
-1 |
-23 |
Розв’язуємо самостійно join.naurok.ua
VII. Підсумок уроку
- Сформулюйте означення кореня n-го степеня із числа а.
- Чи існує корінь парного степеня з від’ємного числа?
- Чому дорівнює добуток коренів n-го степеня?
- Чому дорівнює частка коренів n-го степеня?
- Сформулюйте теорему про корінь з кореня?
VIII. Домашнє завдання
Істер О.С Опрацювати § 4 Виконати № 4.10; 4.12; 4.14; 4.22; 4.26.
1


про публікацію авторської розробки
Додати розробку

-

Шелепа Тетяна
09.10.2022 в 23:35
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Катрін Альона Анатоліївна
31.10.2021 в 21:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сімаченко Олена
04.10.2021 в 10:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Савитская Ирина
30.10.2020 в 14:58
Загальна:
4.0
Структурованість
4.0
Оригінальність викладу
4.0
Відповідність темі
4.0
Показати ще 1 відгук