Опорний конспект з теми "Функції, їхні властивості та графіки"

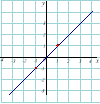
1) Лінійна функція: - пряма

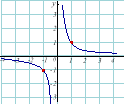
2)  Гіпербола :

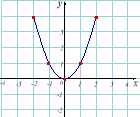
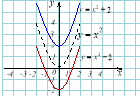
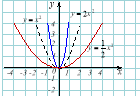
3) Квадратична функція: 

- парабола

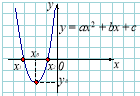
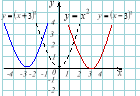
4) Квадратична функція:

- парабола

1) Нулі функції: .

2) Координати вершини:  .

3) Перетин з віссю оу:  х = 0.

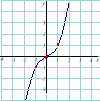
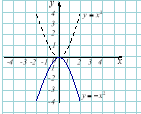
5) Кубічна парабола :

6) - вітка парабола

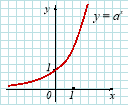
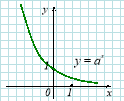
7) Показникова функція (експонента):

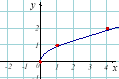
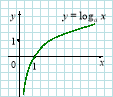
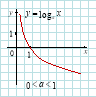
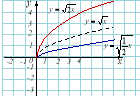
8) Логарифмічна функція:

Тригонометричні функції

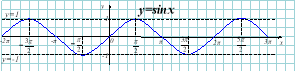
9) Синусоїда:  у=sinx

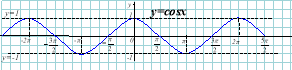
10) Косинусоїда:  у=сosx

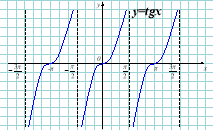
11) Тангенсоїда:  у=tgx

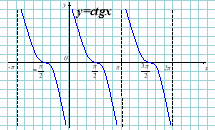
12) Котангенсоїда:  у=сtgx

Геометричні перетворення графіка функції

Функція виду

Перетворення

Приклад

1

Паралельне перенесення графіка функції

уздовж осі оу на відстань b:

- вгору

- вниз

2

Паралельне перенесення графіка функції уздовж осі ох на відстань :

- вліво

- вправо

3

- стиск графіка функції 

вздовж осі ох у k разів;

- стиск графіка функції вздовж осі ох у разів

4

- розтяг графіка функції

вздовж осі оу у с разів;

- стиск графіка функції вздовж осі оу у разів

5

Симетрія графіка функції відносно осі ох.

6

Симетрія графіка функції відносно осі оу.

7

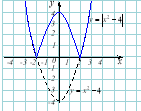
1) Побудувати графік функції ;

 2) частину графіка, що знаходиться нижче від осі ох, симетрично відобразити відносно осі ох.

8

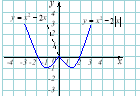
1) Побудувати графік функції ;

2) частину графіка, яка знаходиться ліворуч від осі ординат відкинути, а до тієї частини, що залишилась, добудувати симетричну відносно осі оу.

Характеристика або властивість функції

Геометричний зміст

Графічна ілюстрація

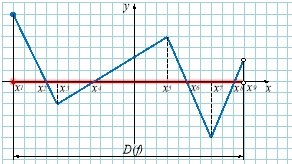
Область визначення : множина значень, яких набуває незалежна змінна х.

Проекція графіка на вісь ох.

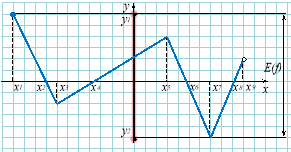
Область значень функції : множина значень, яких набуває залежна змінна у.

Проекція графіка на вісь оу.

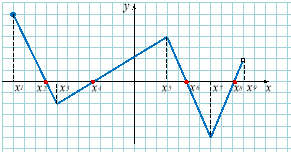
Значення аргументу при яких функція дорівнює нулю називають нулями функції, тобто розв’язок рівняння .

Абсциси точок перетину графіка з віссю ох.

: х = х₂; х₄; х₆; х₈

Проміжками знакосталості функції називають проміжки, на яких функція додатна, або від’ємна:

а) проміжки додатного знаку

б) проміжки від’ємного знаку

Проміжки, на яких графік функції розташований над віссю ох.

Проміжки, на яких графік функції розташований під віссю ох.

:

:

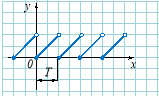
Періодичність

Функція називається періодичною, якщо існує таке число Т ≠ 0, що для всіх х і х ± Т виконується умова: , Т – період.

Графік функції повторюється на кожному проміжку, довжина якого дорівнює періоду функції.

Характеристика або властивість функції

Геометричний зміст

Графічна ілюстрація

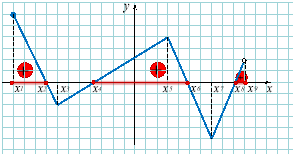
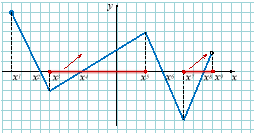
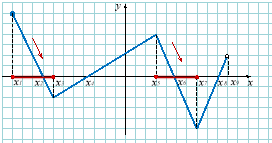
Проміжки монотонності

а) Функція називається зростаючою на деякому проміжку, якщо більшому значенню аргументу відповідає більше значення функції, тобто: якщо х₂>х₁ то .

б) Функція називається спадною на деякому проміжку, якщо більшому значенню аргументу відповідає менше значення функції, тобто: якщо х₂>х₁ то .

Проміжки, на яких графік функції прямує направо вгору.

Проміжки, на яких графік функції прямує направо вниз.

Зростання:

Спадання:

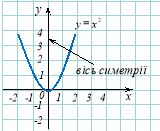
Парність

Функція називається парною, якщо для довільних х та (-х) із області її визначення виконується умова .

Графік парної функції симетричний відносно осі оу.

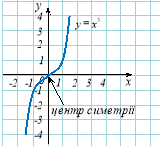
Непарність

Функція називається непарною, якщо для довільних х та (-х) із області її визначення виконується умова .

Графік непарної функції симетричний відносно початку координат.

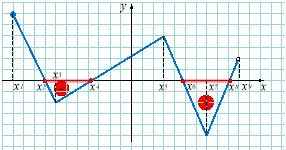
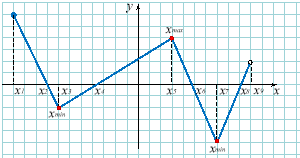
Точки екстремуму:

а) точки максимуму: х_max

б) точки мінімуму: х_min

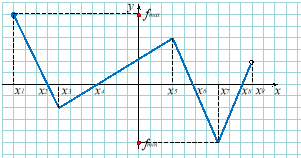
Найбільше f_max та найменше f_min значення функції на проміжку [x₁; x₉)