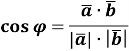Організація дистанційного навчання в ЗНЗ
Метою дистанційного модуля є самостійне опрацювання навчального матеріалу з геометрії в обсязі, визначеному Державним стандартом базової загальної середньої освіти.
Модуль створений згідно з вимогами програмного матеріалу за 9клас, містить три теми і направлений на ефективне формування системи знань, умінь та навичок з даної теми, розроблений як цілісна система управління навчальним процесом особистості і звернена на користувача, реалізацію його можливостей
Для кращого вивчення всього змісту навчального матеріалу виділені ключові питання, неодноразове повернення навчального матеріалу: від простого до складного, від репродуктивних завдань до завдань різного рівня складності, до елементів, що розвивають в учнів здібності, пам'ять, мислення, увагу.
Поданий матеріал знайде свого читача серед учнів, які не мають можливостей відвідувати очні заняття: дітей з особливими потребами, переселенців, осіб, які знаходяться на тимчасово окупованих територіях, тощо.
Учень сам буде оперувати навчальним змістом, що, безумовно, приведе до усвідомленого засвоєння матеріалу.
 ВІДДІЛ ОСВІТИ ПОКРОВСЬКОЇ МІСЬКОЇ РАДИ ДОНЕЦЬКОЇ ОБЛАСТІ
ВІДДІЛ ОСВІТИ ПОКРОВСЬКОЇ МІСЬКОЇ РАДИ ДОНЕЦЬКОЇ ОБЛАСТІ
ЗАГАЛЬНООСВІТНЯ ШКОЛА І-ІІ СТУПЕНІВ №36
«Навчати цікаво – це навчати незвично»
ОРГАНІЗАЦІЯ ДИСТАНЦІЙНОГО НАВЧАННЯ В ЗНЗ
Підготовила
Шидловська В.Д., учитель математики
м. Покровськ,2017
м.
Організація дистанційного навчання в ЗНЗ /Шидловська В.Д., учитель математики загальноосвітньої школи І-ІІ ступенів № 36, - м. Покровськ, 2017. – 31 с.
У посібнику представлено змістовний модуль «Вектори на площині» для організації в ЗНЗ дистанційного навчання
Для вчителів математики, учнів 9 класу та їх батьків
© Шидловська В.Д.
ЗМІСТ
Анотація ......................................4
Вступ .........................................5
- Модуль дистанційного навчання в ЗНЗ................7
- Змістовний модуль «Вектори на площині».............9
-
Інструктивно-методичні матеріали
- Рейтингова система оцінки знань.................10
- Програма модуля «Вектори на площині»............11
- Інформація для опрацювання....................11
-
Основні поняття пов’язані з вектором
- Означення модуля. Модуль і напрям вектора.........12
- Ріні вектори................................13
- Координати вектора..........................14
-
Дії над векторами
- Додавання векторів...........................15
- Віднімання векторів..........................17
- Множення вектора на число.....................18
- Скалярний добуток векторів.......................19
-
Контрольно-оцінювальна діяльність
- Самостійна робота №1........................22
- Самостійна робота №2........................23
- Самостійна робота №3........................25
- Тематична контрольна робота...................26
ІНФОРМАЦІНЕ ЗАБЕЗПЕЧЕННЯ....................27
ДОДАДКИ
Додаток 1...................................28
Додаток 2...................................29
Додаток 3...................................30
АНОТАЦІЯ
Метою дистанційного модуля є самостійне опрацювання навчального матеріалу з геометрії в обсязі, визначеному Державним стандартом базової загальної середньої освіти.
Модуль створений згідно з вимогами програмного матеріалу за 9клас, містить три теми і направлений на ефективне формування системи знань, умінь та навичок з даної теми, розроблений як цілісна система управління навчальним процесом особистості і звернена на користувача, реалізацію його можливостей
Для кращого вивчення всього змісту навчального матеріалу виділені ключові питання, неодноразове повернення навчального матеріалу: від простого до складного, від репродуктивних завдань до завдань різного рівня складності, до елементів, що розвивають в учнів здібності, пам’ять, мислення, увагу.
Поданий матеріал знайде свого читача серед учнів, які не мають можливостей відвідувати очні заняття: дітей з особливими потребами, переселенців, осіб, які знаходяться на тимчасово окупованих територіях, тощо.
Учень сам буде оперувати навчальним змістом, що безумовно приведе до усвідомленого засвоєння матеріалу.
ВСТУП
У нормативно-правових документах чинного законодавства констатовано, що для реалізації інтелектуального потенціалу нації та міжнародної конкурентоспроможності держави рівень комп’ютерної та інформаційної грамотності, впровадження сучасних ІКТ в управління соціальною сферою є недостатнім.
Згідно із основними положеннями Національної програми інформатизації та нагальними потребами сучасності, втілення в життя головних засад означеного вище процесу передбачає створення найближчим часом єдиного інформаційного освітнього простору, одним із завдань якого є розробка електронного освітнього контенту для учнів, запровадження навчання на засадах дистанційних технологій, створення умов для мережевого спілкування всіх учасників освітнього процесу в будь-якому місці і в будь-який час, незалежно від форми їх навчання.
Ситуація, яка склалася в Донецькій та Луганській областях в галузі освіти під час проведення АТО, вимагає від освітян оперативно реагувати на ці виклики та прискорити роботу щодо розвитку дистанційного навчання на означених територіях як найбільш ефективної форми отримання освіти в таких умовах.
Одним з виходів в даній ситуації може стати широке застосування в системі загальної середньої освіти елементів дистанційного навчання. Головною метою тут повинно стати створення умов для забезпечення якісної допрофільної та профільної підготовки учнів загальноосвітніх навчальних закладів на дистанційній основі, надання їм можливості отримати основні або додаткові знання на засадах інформаційно-комунікаційних технологій.
Актуальність цих дій визначається потребою подальшої модернізації навчально-методичного, науково-методичного, інформаційного та програмно-технічного забезпечення дистанційного навчання та необхідністю створення варіативних моделей дистанційного навчання в єдиному освітньому просторі регіону для забезпечення реалізації концепції неперервності освіти дітей та дорослих.
- Модель дистанційного навчання в ЗНЗ
![]()
![]()
![]()






![]()




![]()




![]()
Адміністратор СДН – той, хто забезпечує стабільне функціонування системи, вирішує технічні питання, слідкує за статистикою роботи системи.
Організатор навчання – той, хто планує навчальну діяльність, розробляє програми навчання, займається розподілом учнів за групами і навчальним навантаженням на тьютера (учителя), вирішує різні організаційні питання.
Тьютер – той, хто навчає.
Учень – той, хто навчається
|
Дистанційне навчання |
||
|
Відкрите навчання |
|
Сучасні телекомунікації |
|
Комп’ютерні навчальні програми |
Електронна пошта, телеконференції, список розсилок, Web |
|
|
Свобода вибору місця, часу, темпу та форми навчання |
Контроль знань, тести, тренажери, мультимедійні та моделюючі програми, ігри |
|
- Змістовний модуль « Вектори на площині»
В процесі вивчення теми учні повинні:
- Мати уяву про поняття пов’язані з вектором.
- Знати:
- правила додавання і віднімання векторів;
- властивості дій над векторами;
- властивості колінеарних векторів;
- властивості скалярного добутку векторів.
- Вміти:
- знаходити координати і довжину вектора;
- виконувати дії над векторами, заданими координатами та геометрично (малюнком);
- застосовувати вектори до розв’язку задач.
Успішне вивчення теми дозволить учням:
Описувати вектор, модуль і напрям вектора, координати вектора, дії над векторами, рівність і колінеарність векторів.
Відкладати вектор, рівний даному; вектор, рівний сумі (різниці) векторів
Формулювати:
- властивості дій над векторами;
- означення скалярного добутку векторів, його властивості.
Застосовувати вивчені означення і властивості до розв’язування задач.
Ключові слова:вектор, нульовий вектор, одиничний вектор, модуль і напрям вектора, координати вектора, рівність і колінеарність векторів, правило «трикутника», правило «паралелограма», скаляр, скалярний добуток
-
 Інструктивно-методичні матеріали
Інструктивно-методичні матеріали
|
|
Кількість балів |
|
Самостійна робота №1 |
3 |
|
Самостійна робота №2 І рівень |
5 |
|
ІІ рівень |
8 |
|
ІІІ рівень |
9 |
|
ІV рівень |
8 |
|
Самостійна робота №3 |
9 |
|
Всього |
42 |
Таблиця переводу набраних балів в оцінку
|
Кількість балів |
Оцінка |
|
1-2 |
1 |
|
3-6 |
2 |
|
7-10 |
3 |
|
11-14 |
4 |
|
15-18 |
5 |
|
19-22 |
6 |
|
23-26 |
7 |
|
27-30 |
8 |
|
31-34 |
9 |
|
35-38 |
10 |
|
39-40 |
11 |
|
41-42 |
12 |
![]() 3.2 Програма модуля. Вектори на площині.
3.2 Програма модуля. Вектори на площині.
Тема 1. Основні поняття, пов’язані з вектором.
Тема 2. Дії над векторами
Тема 3. Скалярний добуток векторів.
3.3.Інформація для опрацювання
У процесі вивчення змістового модуля «Вектори на площині» важливо уточнити й узагальнити власні знання щодо векторів. Для кращого розуміння питання додаються опорні конспекти (Додатки 1,2,3).
Вивчаючи §1, особливу увагу приділіть визначенню понять пов’язаних з вектором. Запам’ятайте, що вектор, який задано координатами побудувати на площині неможливо. Для побудови вектора потрібно знати координати точок його початку і кінця. Переглянь Додаток 1.
Вивчаючи §2, зверніть увагу на те, що при додаванні, відніманні векторів та при множенні вектора на число, отримуємо новий вектор. Віднімання векторів можна замінити додаванням. Переглянь Додаток 2.
Вивчаючи §3, проаналізуйте отримані результати при скалярному множенні векторів. Особливу увагу приділіть знаходженню кута між векторами. Переглянь Додаток 3.
Після опрацювання кожного з параграфів, дайте відповіді на запропоновані «Питання для самоконтролю» (у разі виникнення утруднень з відповіддю знайдіть її в тексті лекції або в підручнику ![]() ).
).
За змістом матеріалу лекції виконайте запропоновані завдання.
4. Основні поняття, пов’язані з вектором.
4.1.Означення модуля. Модуль і напрям вектора.
У природничих науках зустрічаються величини, які повністю характеризуються Числовими значеннями, - довжина, площа, температура тощо (такі величини називають скалярними). Але чимало чимало величин задаються не тільки числовим значенням, але й напрямом. Наприклад, для розв’язування задачі про рух недостатньо знайти його швидкість – треба уточнити в якому напрямі він рухається. У такому випадку швидкість автомобіля розглядається яв векторна величина. Отже, векторна величина характеризується числовим значенням і напрямом. У геометрії векторні величини зображають за допомогою напрямлених відрізків.
![]() Означення
Означення
Вектором називається напрямлений відрізок, тобто для якого вказано, який із його кінців є початком, а який – кінцем.
Зазвичай вектор зображають відрізком зі стрілкою, яка вказує напрям вектора. Для позначення векторів використовують малі латинські букви (a, b, c, d …) або дві великі латинські букви, перша з яких позначає початок вектора, а друга – кінець. Замість слова «вектор» над позначенням вектора ставлять стрілку.
![]() Означення
Означення
Довжиною ( або модулем) вектора ![]() називається довжина відрізка АВ, що зображує вектор. Довжина вектора
називається довжина відрізка АВ, що зображує вектор. Довжина вектора![]() позначається так:
позначається так: ![]()
![]() Означення
Означення
Нульовим вектором називається вектор, початок і кінець якого збігаються
Таким чином, будь-яку точку А площини можна вважати нульовим вектором ![]() . Нульовий вектор позначають так:
. Нульовий вектор позначають так: ![]() Напряму він не має, а його довжина дорівнює нулю:
Напряму він не має, а його довжина дорівнює нулю: ![]() =0.
=0.
![]() Означення
Означення
Ненульові вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.
Нульовий вектор вважають колінеарним будь-якому вектору.
![]() Означення
Означення
Вектори ![]() і
і ![]() називаються співнапрямленими (або однаково напрямленими), якщо промені AB і CD співнапрямлені. Вектори
називаються співнапрямленими (або однаково напрямленими), якщо промені AB і CD співнапрямлені. Вектори ![]() і
і ![]() називаються протилежно напрямленими, якщо промені AB і CD протилежно напрямлені.
називаються протилежно напрямленими, якщо промені AB і CD протилежно напрямлені.
![]()
![]()
![]()
![]() Це позначають так:
Це позначають так: ![]()
![]() – співнапрямлені;
– співнапрямлені; ![]()
![]() – протилежно напрямлені.
– протилежно напрямлені.
4.2.Рівні вектори
![]() Означення
Означення
Два вектори називаються рівними, якщо вони суміщаються паралельним перенесенням.
Оскільки вектори можуть бути задані геометрично або своїми координатами, то і означення рівних векторів буде різним. (Додаток 1.)
Основні властивості і ознаки рівних векторів:
- Рівні вектори співнапрямлені і мають рівні довжини.
- Якщо вектори співнапрямлені і мають рівні довжини, то вони рівні.
- Від будь-якої точки можна відкласти вектор, що дорівнює даному, і при тому тільки один.
4.3. Координати вектора
![]() Означення
Означення
Координатами вектора з початком А(XА; YA) і кінцем В(XВ; YВ) називають числа а1= XB – XA і а2 = YВ – YA.
Інакше кажучи, кожна координата вектора дорівнює різниці відповідних координат його кінця і початку.
Координати вектора записуються у вигляді: ![]() (а1;а2) або, наприклад,
(а1;а2) або, наприклад, ![]() .
.
Таким чином, координати вектора не фіксують напрямлений відрізок, а лише задають його довжину і напрям.
Як приклад застосування рівності координат векторів наведемо ще один спосіб розв’язування відомої задачі про пошук четвертої вершини паралелограма.
|
Задача |
|
|
А D Рис.1 |
Дано: АВСD – паралелограм, А(–2;1), В(0;4), С(4;1). Знайдіть координати точки D(х;у). |
|
Розв’язання.
Якщо чотирикутник АВСD – паралелограм (Рис.1), то
Отже,
Відповідь: D(2; |
|
![]() Перевір себе
Перевір себе
- Дайте означення вектора. Як зображають вектор?
- Що таке довжина вектора? Який вектор називають нульовим?
- Які вектори називають співнапрямленими; протилежно напрямленими; колінеарними.
- Дайте означення рівних векторів.
- Як визначити координати вектора? Як пов’язані координати рівних векторів?
- Якими способами можна задати вектор?
5. Дії над векторами
5.1.Додавання векторів
Для векторів, як і для чисел, визначаються операції додавання і віднімання, при чому результатами цих дій також є вектори.
![]() Означення
Означення
Сумою векторів ![]() (а1;а2) і
(а1;а2) і ![]() (b1; b2) називається вектор
(b1; b2) називається вектор ![]() (с1; с2) з координатами с1 = а1 + b1; с2 = а2 + b2
(с1; с2) з координатами с1 = а1 + b1; с2 = а2 + b2
Властивості додавання векторів.
Для будь яких векторів ![]() (а1;а2);
(а1;а2);![]() (b1; b2)
(b1; b2)![]() (с1; с2):
(с1; с2):
-
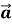 +
+ 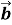 =
= 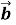 +
+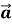 ;
;
-
(
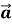 +
+ 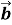 ) +
) +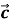 =
= 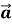 +(
+( 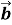 +
+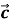 );
);
-
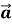 +
+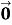 =
= 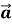 .
.
Для доведення цих властивостей достатньо порівняти координати векторів у правій і лівій частинах кожної рівності. Очевидно, що ці координати рівні, отже, рівні і самі вектори.
У який спосіб можна побудувати зображення вектора-суми за зображеннями векторів-доданків? Для відповіді на це питання доведемо наступну теорему.
|
Теорема (про додавання векторів) Для будь-яких точок А, В і С справджується векторна рівність
|
|
|
Рис.2
|
Доведення
Нехай дано точки А(х1;у1); В(х2;у2); С(х3;у3) (Рис.2). Виразивши координати векторів-доданків, маємо
х2
у2
Отже, координати вектора-суми збігаються з координатами вектора |
Наслідками цієї теореми є такі способи побудови суми векторів:
- Правило трикутника.
- Правило паралелограма.
- Правило многокутника.
Переглянь ![]() та презентацію Додавання і віднімання векторів https://cloud.mail.ru/public/9ZcH/a3QS2buER
та презентацію Додавання і віднімання векторів https://cloud.mail.ru/public/9ZcH/a3QS2buER
5.2. Віднімання векторів
![]() Означення
Означення
Різницею векторів ![]() (а1;а2) і
(а1;а2) і ![]() (b1; b2) називається такий вектор
(b1; b2) називається такий вектор ![]() (с1; с2), який у сумі з вектором
(с1; с2), який у сумі з вектором ![]() дає вектор
дає вектор ![]() :
: ![]() +
+ ![]() =
= ![]() .
.
|
|
Відкладемо вектори |
![]() Означення
Означення
Протилежними векторами називаються два протилежно напрямлені вектори однакової довжини.
![]() і
і ![]() протилежні вектори. Вектор, протилежний вектору
протилежні вектори. Вектор, протилежний вектору ![]() , позначають
, позначають ![]()
![]() . Очевидно, що
. Очевидно, що ![]() + (
+ (![]()
![]() ) = 0. Для отримання різниці векторів
) = 0. Для отримання різниці векторів ![]()
![]()
![]() можна додати до вектора
можна додати до вектора ![]() вектор, протилежний вектору
вектор, протилежний вектору ![]()
Переглянь презентацію Додавання і віднімання векторів.pptx
![]() Перевір себе
Перевір себе
- Дайте означення суми двох векторів. Опишіть способи побудови вектора – суми.
- Дайте означення різниці двох векторів. Опишіть способи побудови вектора – різниці.
5.3. Множення вектора на число
![]() Означення
Означення
Добутком вектора ![]() (а1;а2) на число k (або добутком числа k на вектор
(а1;а2) на число k (або добутком числа k на вектор ![]() ) називається вектор k
) називається вектор k![]() =
= ![]()
Cформулюємо властивості множення вектора на число
Для будь-яких векторів ![]() і
і ![]() та чисел k, m:
та чисел k, m:
|
4) |
|
5)(k + m) |
|
6) k( |
Теорема (про довжину і напрям вектора k![]() )Довжина вектора k
)Довжина вектора k![]() дорівнює
дорівнює ![]() . Якщо
. Якщо![]() ≠
≠ ![]() , то вектор k
, то вектор k![]() спів напрямлений з вектором
спів напрямлений з вектором ![]() за умови k
за умови k![]()
![]() за умови k
за умови k![]()
Наслідок (властивість і ознака колінеарних векторів)
- у колінеарних векторів відповідні координати пропорційні;
- якщо у двох векторів відповідні координати пропорційні, то ці вектори колінеарні Додаток 3.
Задача. Вектори ![]() і
і ![]() (
(![]()
Розв’язок. Оскільки вектори колінеарні, то їх відповідні координати пропорційні. Складемо і розв’яжемо рівняння:
![]() =
= ![]() ;
;
x = 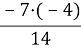 ;
;
х = 2. Відповідь: 2
6. Скалярний добуток векторів
![]() Означення
Означення
Скалярним добутком векторів ![]() (а1;а2) і
(а1;а2) і ![]() (b1; b2) називається число a1b1 + a2b2
(b1; b2) називається число a1b1 + a2b2
Сформулюємо властивості скалярного множення векторів.
Для будь яких векторів ![]() і
і ![]() та числа k:
та числа k:
-
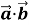 =
= 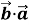 ; 2) (k
; 2) (k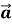 )
)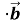 = k (
= k (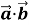 ); 3) (
); 3) (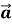 +
+ 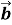 )
)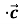 =
= 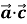 +
+ 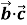
Доведіть ці рівності самостійно на підставі означення скалярного добутку векторів.
Скалярний добуток ![]() називають скалярним квадратом вектора
називають скалярним квадратом вектора ![]() і позначають
і позначають ![]() 2. Очевидно, що
2. Очевидно, що ![]() 2 = a12 + a22 =
2 = a12 + a22 = ![]() 2.
2.
![]() Означення
Означення
Кутом між ненульовими векторами ![]() і
і ![]() називається кут АВС.
називається кут АВС.
 В
В
![]() А ) С
А ) С
Кутом між довільними ненульовими векторами ![]() і
і ![]() називається кут між векторами, що дорівнюють даним векторам і мають спільний початок.
називається кут між векторами, що дорівнюють даним векторам і мають спільний початок.

![]()
![]() )
) ![]()
Теорема (про скалярний добуток векторів)
Скалярний добуток векторів дорівнює добутку їх довжин на косинус кута між ними: ![]() =
= ![]() (
(![]() )
)
Доведення дивись ![]() .
.
Наслідок 1
Якщо ![]() – ненульові вектори, то
– ненульові вектори, то ![]() (
(![]() ) =
) = ![]() .
.
Наслідок 2 (властивість і ознака перпендикулярних векторів)
Якщо вектори перпендикулярні, то їх скалярний добуток дорівнює нулю, і навпаки: якщо для ненульових векторів скалярний добуток дорівнює нулю, то вектори перпендикулярні. Додаток 3
Задача. При якому значенні x вектори ![]() і
і ![]() (3;x) перпендикулярні?
(3;x) перпендикулярні?
Розв’язок. Оскільки дані вектори перпендикулярні, то їх скалярний добуток дорівнює нулю. Складемо і розв’яжемо рівняння:
2·3 = 1·х;
х = 6.
Відповідь: 6
![]() Перевір себе
Перевір себе
-
Дайте означення добутку вектора на число. Сформулюйте теорему про довжину і напрям вектора k
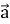 .
.
- Дайте означення скалярного добутку векторів. Як визначається кут між векторами?
- Сформулюйте властивість і ознаку колінеарних векторів.
- Сформулюйте теорему про скалярний добуток векторів
- Сформулюйте властивість і ознаку перпендикулярних векторів.
![]() 7. Контрольно-оцінювальна діяльність
7. Контрольно-оцінювальна діяльність
7.1. Самостійна робота №1 Скільки різних векторів зображено на кожному малюнку?
Варіант 1
|
А) |
Б) |
В) |
|
В С
А D |
А D |
E F O C
A B |
|
1 – один; |
1 – чотири; |
1 – три; |
Варіант 2
|
А) |
Б) |
В) |
|
A D |
A C
D |
A D |
|
1 – один; |
1 – чотири; |
1 – два; |
Початковий рівень складності. Виконайте дії
І варіант
-
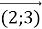 +
+ 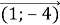 =
= 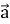
-
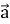 -
- 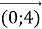 =
= 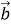
-
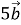 =
= 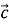
-
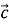 (2;0) =
(2;0) = 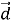
-
-3
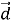 =
= 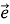
Код остаточної відповіді – 36840
ІІ варіант
-
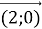 +
+ 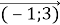 =
= 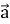
-
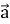 -
- 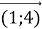 =
= 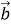
-
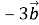 =
= 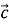
-
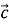 (-2;3) =
(-2;3) = 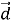
-
-2
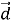 =
= 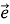
Код остаточної відповіді – 79521
|
Відповідь |
- 18 |
9 |
|
30 |
|
|
|
|
|
-90 |
|
Код |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
Середній рівень складності Тестування. (Оберіть вірну відповідь)
-
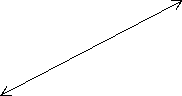
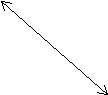
За малюнком знайдіть суму векторів: a)
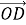 +
+ 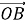 ; b)
; b) 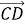 +
+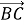 .
.
![]()
![]()
![]()
 B C
B C
![]() A D
A D
|
a) |
b) |
|
1). |
1). |
|
2). |
2). |
|
3). |
3). |
|
4). |
4). |
2. Модуль вектора ![]() (5;n) дорівнює 13. Знайдіть n.
(5;n) дорівнює 13. Знайдіть n.
|
1). 8; |
|
2). 12; |
|
3). |
|
4). |
3. Відомо, що вектори ![]() і
і ![]()
![]()
|
1). 0; |
|
2). |
|
3). |
|
4). |
4. Дано точки А(2;3) та В(- 2;0). Знайти а) координати вектора ![]() ; b)
; b) ![]()
|
а) |
b) |
|
1). |
1). 5; |
|
2). |
2). 3; |
|
3). |
3). – 3; |
|
4). |
4). 1. |
Достатній рівень складності
- Знайдіть будь-який кут ∆АВС, якщо А(0;1); В(1;0); С(4;4).
- Знайдіть діагоналі паралелограма, якщо вони відносяться як 3:5, а довжини сторін паралелограма дорівнюють 8 см та 19 см.
- Сторони паралелограма відносяться як 1:2. Знайдіть довжини сторін, якщо діагоналі паралелограма дорівнюють 9 см та 12 см.
Високий рівень складності
-
Дано три точки О; А; В. Точка М ділить відрізок АВ у відношенні µ
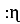
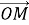 через вектори
через вектори 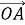 =
= 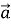 і
і 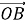 =
= 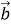
- Доведіть, що медіани трикутника перетинаються в точці, яка ділить їх у відношенні 2:1 рахуючи від відповідних вершин .
![]() 7.3. Самостійна робота №3
7.3. Самостійна робота №3
- Закінчіть речення: "Якщо скалярний добуток дорівнює нулю, то..."
- Закінчіть речення: "Якщо вектори перпендикулярні, то їх скалярний добуток..."
-
Чому дорівнює кут між ненульовими векторами,
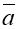 і
і 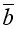 , якщо
, якщо 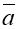
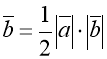 .
.
-
Скалярний квадрат вектора
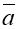 =16 . Чому дорівнює модуль вектора
=16 . Чому дорівнює модуль вектора 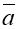 ?
?
-
Чи перпендикулярні вектори
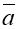 (2;3) і
(2;3) і 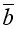 (3;-2)
(3;-2)
-
Дано ромб ABCD, діагоналі якого перетинаються в точці О, АВ=BD. Знайдіть кут між векторами
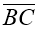 і
і 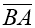 .
.
- Доведіть, що діагоналі прямокутника рівні
Алгоритм рішення
-
Позначте сторони прямокутника:
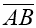 =
=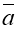 ,
, 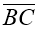 =
=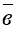 .
.
-
Виразіть вектори
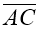 і
і 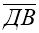 через вектори
через вектори 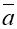 і
і 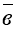 .
.
- Знайдіть квадрати діагоналей за властивістю скалярного добутку.
- Зробіть висновки.
![]() 7.4. Тематична контрольна робота Вектори на площині
7.4. Тематична контрольна робота Вектори на площині
Перший варіант
|
3б. |
6б. |
9б. |
12б. |
|
№1.Побудуйте вектор |
|
№1.Дано паралелограм ABCD. Знайдіть суму векторів |
№1. AD – медіана ∆АВС. Доведіть, що |
|
№2. Знайдіть координати вектора |
№2. Знайдіть координати вектора |
№2. В ∆АВС NM – середня лінія. Знайти координати вектора |
№2. AD – медіана ∆АВС з вершинами А(-2;7);В(3;-2), С( 9;4). Знайдіть модуль вектора |
|
№3. Знайдіть вектор |
№3. Знайдіть скалярний добуток векторів |
№3. Знайдіть кут між векторами |
№3. Вектор |
|
Другий варіант |
|||
|
3б. |
6б. |
9б. |
12б. |
|
№1. Побудуйте вектор |
|
№1. Дано паралелограм ABCD. Виразіть вектор |
№1. Доведіть теорему про середню лінію трикутника за допомогою векторів. |
|
№2. Знайдіть координати вектора |
№2. Знайдіть координати вектора |
№2. В ∆АВС NM – середня лінія. Знайти координати вектора |
№2. AD – медіана ∆АВС з вершинами А(0;7);В(5;-2),С( 11;4). Знайдіть модуль вектора |
|
№3. Знайдіть вектор |
№3.Знайдіть скалярний добуток векторів |
№3. Знайдіть кут між векторами |
№3. Дано рівносторонній ∆АВС, сторона якого дорівнює 1. Позначивши |
- ІНФОРМАЦІЙНЕ ЗАБЕЗПЕЧЕННЯ
![]() Використані джерела
Використані джерела
- А.П.Єршова, В.В. Голобородько, О.Ф. Крижановський, С.В.Єршов Геометрія.9 клас: Підруч. для навч. закл. – Х.: Вид-во «Ранок», 2009. – 256с.:іл.

- Мерзляк А.Г., Полонський В.Б., Якір М.С.Геометрія 9клас: Підруч. для навч. закл. – Х.: Вид-во «Гімназія», 2009. – 268с.
-
https://www.youtube.com/watch?v=yssg8G1HyQ4
- https://cloud.mail.ru/public/9ZcH/a3QS2buER
 Основні поняття пов’язані з вектором Додаток 1
Основні поняття пов’язані з вектором Додаток 1
|
Вектор
В А
|
|
|
|
координатами
|
геометрично
В A |
|
|
|
||
|
|
- рівні вектори мають рівні відповідні координати; - однаково направлені; - рівні за модулем. |
|
|
- мають протилежні координати;
- протилежно напрямлені; - рівні за модулем |
||
Дії над векторами Додаток 2
 В результаті цих дій отримуємо новий вектор
В результаті цих дій отримуємо новий вектор
|
Сума векторів – це новий вектор! Правило трикутника
|
Різниця векторів – це новий вектор!
Віднімання векторів заданих координатами
Якщо |
Добуток вектора на число – це новий вектор
|
|
Правило паралелограма
|
|
|
|
Додавання векторів заданих координатами
Якщо |
Для будь-яких точок А, В і С справджується
векторна рівність
А С |
|
Скалярний добуток векторів
 Додаток 3
Додаток 3
|
Колінеарні вектори
b
a||b
|
Скалярний добуток векторів – це число (скаляр)
Скалярний квадрат
|
Перпендикулярні вектори
|
ДЛЯ НОТАТОК
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

1


про публікацію авторської розробки
Додати розробку