Урок з геометрії у 9 класі "Відстань між двома точками із заданими координатами"

9 клас. Геометрія

Тема уроку. Відстань між двома точками із заданими координа­тами.

Мета уроку: виведення формули для знаходження відстані між двома точками, заданими координатами, і застосування формул до розв'язування задач; розвивати вміння бачити закономірності, міркувати за аналогією; виховувати позитивне ставлення до навчання, уважність.

Хід уроку

Учітесь, читайте,

І чужому научайтесь,

Й свого не цурайтесь.

Т. Г. Шевченко

І. Організаційний момент.

ІІ. Перевірка домашнього завдання.

Хвилинка економії.

Однією з важливих проблем сьогодення є збереження використання води, плата за постачання якої невпинно зростає і б’є по гаманцям споживачів. Порахуємо разом.

Цівка води товщиною в сірник за тиждень може призвести до втрат 480л води. Скільки літрів води буде втрачено за тиждень, якщо залишаться не до кінця закритими крани в їдальні?

480*8=3840л

Скільком мешканцям вистачило б цієї води, якщо мінімальна її потреба для однієї людини 30л на добу?

3840/30=128чол.

Перевірка виконання домашнього завдання.

Перевірка за зразком на дошці.

IIІ. Актуалізація опорних знань.

Завдяки математичним перетворенням ви зможете дати відповідь про деякі епізоди життя Т.Г. Шевченка.

Тарас Григорович Шевченко із  років життя років був на засланні, роки був кріпаком і лише років був на волі.

IV. Оголошення теми і мети уроку.

Не завжди довжину відрізка можна дізнатися, приклавши лінійку. Коли ми говоримо про метод координат, ми можемо сказати, що за допомогою цього методу можна знайти великі відстані у двовимірному просторі, маючи координати точок, що є основою для знаходження відстаней між точками у просторі.

V. Засвоєння нових знань

Виведення формули відстані між двома точками, які задані своїми координатами, можна здійснити з використанням підручника с. 85.

Розв'язування задач

1. Виконання вправи 280 (а), с. 88
2. Знайдіть довжину відрізка ВС, який у двічі більший за відрізок АМ із заданими координатами кінців відрізка: А(5; 0), М(0;12).

Коли ви дізнаєтесь відповідь задачі, то зможете сказати у скільки років Т.Г. Шевченко видав свою першу збірку поезій, яка дала початок новому періоду в історії української літератури. (26 років).

3. А скільки ж творів ввійшло до першої збірки великого Кобзаря? Дізнаємося це, розв’язавши слідуючу задачу: знайти  х, якщо відстань між точками М(4; 5) і N(х; 2) дорівнює 5.(х=8).

IIІ. Закріплення та осмислення нового матеріалу

Виконавши тести ми згадаємо, за скільки Т.Г.Шевченка було викуплено з кріпацтва.

Тести.

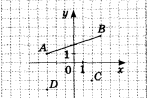1. Яка точка має координати (2;-2)?

А) А - 1,            Б) В - 3,              В) С - 2,           Г) D – 4.

     2. Укажіть координати середини відрізка АВ.

А) (0;0) - 4,       Б) (2;0) - 3,      В) (0;2) - 5,         Г) (0;1) – 0.

     3. Знайдіть відстань між точками А і D.

                       А) 1 - 4,              Б) 3 - 5,                В) 4 - 0,               Г) 2 – 5.

                             4. Знайдіть відстань від точки А до початку координат.

                        А) 10 - 4,      Б) - 0,             В) - 5,               Г) 2 – 7.

                           (В.А. Жуковський «… улаштував лотерею на 2500 карбованців асигнаціями…» за власний портрет, написаний великим художником  К.П.Брюлловим. На ці кошти було викуплено Тараса Григоровича Шевченка з кріпацтва).

IV. Домашнє завдання

1. Прочитати п. 8.3, вивчити формулу.
2. Виконати письмові вправи 280 (б) і 281 (а).

V. Підбиття підсумків уроку

Запитання до класу

1. Як знайти відстань між двома точками на координатній прямій?
2. Як знайти відстань між двома точками на координатній пло­щині?

Оцінювання.