Організація самостійної діяльності учнів на уроці "Розв'язування задач. Самостійна робота" при вивченні теми "Паралельність прямих і площин у просторі", 10 клас
Уміння мислити логічно, виконувати висновки без наочної опори, зіставляти думки за певними правилами – необхідна умова успішного засвоєння учбового матеріалу Розвиток мислення, вдосконалення розумових операцій, здібностей міркувати прямим образом залежить від методів навчання.
Тема: Розв’язування задач. Самостійна робота.
Перевірка домашньої роботи
Засвоєння доведення наслідків з аксіом стереометрії перевіряються у вигляді гри « Мозаїка» за картками
Картка 1
|
|
Початок твердження |
Кінець твердження |
|
1 |
АВ – пряма, точка С |
Аксіома |
|
2 |
Прямі АВ і АС різні, оскільки… |
|
|
3 |
Проведемо площину α через прямі АВ і АС |
… площини α і α ' перетинаються по прямій, що проходить через точки А, В і С |
|
4 |
Площина α – шукана, оскільки… |
Аксіома I |
|
5 |
Припустимо, що існує площина α ' така, що… |
Площина α – єдина |
|
6 |
Точки А, В і С – спільні, точки площин α та α ' , отже… |
АВ |
|
7 |
Дістали протиріччя з… |
…точка С не належить прямій АВ |
|
8 |
Висновок |
… умовою теореми |
Картка 2
|
|
Початок твердження |
Кінець твердження |
|
1 |
Проведемо прямі АВ і АС; вони різні, оскільки… |
… умовою теореми |
|
2 |
Через прямі АВ і АС проведемо площину α |
… точки А, В і С |
|
3 |
Припустимо, що існує площина α ', яка містить… |
Площина α – єдина |
|
4 |
Точки А, В, і С – спільні точки площин α і α ', отже… |
Аксіома |
|
5 |
Дістали протиріччя з… |
… площини α і α ' перетинаються по прямій, що проходить через точки А, В і С |
|
6 |
Висновок |
…точки А, В і С за умовою не лежать на одній прямій |
Актуалізація опорних знань
Фронтальне опитування
1) Чи правильно, що всi точки простору належать однiй площинi?
2) Чи можуть двi рiзнi площини мати спiльну точку, але не мати спiльної прямої?
3) Чи правильно, що якщо двi рiзнi площини мають три спiльнi точки, то цi точки лежать на однiй прямiй?
4) Чи правильно, що якщо кiнцi вiдрiзка лежать у площинi, то i його середина лежить у цiй площинi?
5) Чи можуть двi прямi мати спiльну точку, але не лежати в однiй площинi?
6) У просторi дано пряму i точку. Скiльки рiзних площин можна провести через них? Розгляньте всi можливi випадки.
Формування навичок застосування аксіом стереометрії та наслідків з них
 Розв’язування задач iз використанням готових рисункiв
Розв’язування задач iз використанням готових рисункiв
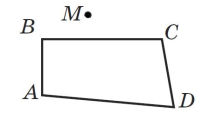 №1. Чи належить точка K площинi паралелограма ABCD, якщо точка N належить вiдрiзку AD, а точка M — вiдрiзку BC?
№1. Чи належить точка K площинi паралелограма ABCD, якщо точка N належить вiдрiзку AD, а точка M — вiдрiзку BC?
№2. Точка M не належить площинi чотирикутника ABCD. Знайдiть пряму перетину площин MAB i MBC.
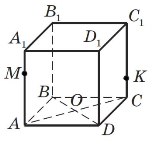 №3. Користуючись рисунком, знайдiть:
№3. Користуючись рисунком, знайдiть:
а) точку перетину прямої AD iз площиною D1C1C
б) точку перетину прямої MC iз площиною B1BC1
в) лiнiю перетину площин MA1B i AA1D
г) лiнiю перетину площин MC1K i B1BC
д) лiнiю перетину площин MBD i AA1C .
Контроль знань Самостійна робота Варіант І
|
І рівень (3 бали) |
|||
|
Виберіть правильну відповідь |
|||
|
1.Дві різні площини можуть мати |
|||
|
А) тільки одну спільну точку |
Б) тільки дві спільні точки |
В) тільки три спільні точки |
Г) безліч спільних точок |
|
2. Якщо через дві прямі можна провести площину, то вони: |
|||
|
А) перетинаються |
Б) співпадають
|
В) не перетинаються , але паралельні |
Г) не перетинаються і не паралельні |
|
3. Дві суміжні вершини і точка перетину діагоналей паралелограма лежать у площині |
|||
|
А) не лежать у площині
|
Б) можуть не лежати у площині |
В) обов’язково лежать у площині |
Г) тільки одна з двох вершин лежить у площині |
|
ІІ рівень (3 бали) |
|||
|
1. Точка А належить площині |
|||
|
2. Площини |
|||
|
3. У просторі проведено прямі, що перетинають прямі a і b, які перетинаються в точці А, в точках, відмінних від точки А. Доведіть, що всі такі прямі лежать в одній площині. |
|||
|
ІІІ рівень (3 бали) |
|||
|
1. Прямі a і b не лежать в одній площині. Прямі c і d перетинають кожну з прямих a і b. Доведіть, що прямі c і d не перетинаються. |
|||
|
2. Дано дві прямі, через які не можна провести площину. Доведіть, що ці прямі не перетинаються. |
|||
|
IV рівень (3 бали) |
|||
|
1. Площина |
|||
Варіант ІІ
|
І рівень (3 бали) |
||||||
|
Виберіть правильну відповідь |
||||||
|
1. Якщо через дві прямі можна провести площину,то: |
||||||
|
А) прямі завжди перетинаються
|
Б) прямі можуть перетинатися або бути паралельними |
В) прямі завжди паралельні
|
Г) прямі не можуть перетинатися
|
|||
|
2. Через пряму a і точку А можна провести дві різні площини, тоді: |
||||||
|
А) площини перетинаються по прямій a , що не проходить через точку А |
Б) площини не можуть бути різними |
В) точка А належить прямій a |
Г) правильної відповіді не має.
|
|||
|
3. З чотирьох точок M, N, K, L жодні три не лежать на одній прямій. Тоді ці чотири точки: |
||||||
|
А) завжди лежать в одній площині |
Б) ніколи не лежать в одній площині |
В) можуть лежати в одній площині |
Г) визначають єдину площину |
|||
|
ІІ рівень (3 бали) |
||||||
|
1. Доведіть, що через дві довільні точки можна провести хоча б одну площину. |
||||||
|
2. Доведіть, що якщо прямі MN і KL не лежать в одній площині, то прямі MK і NL також не лежать в одній площині |
||||||
|
3. Прямі a та b перетинаються в точці О. Доведіть, що всі прямі, які перетинають пряму b та проходять через точку прямої a, відмінну відточки О, лежать у одній площині. |
||||||
|
ІІІ рівень (3 бали) |
||||||
|
1. Площини |
||||||
|
2. Точка А не лежить на прямій а. Доведіть, що всі прямі, які проходять через точку А та перетинають пряму а, лежать водній площині. |
||||||
|
IV рівень (3 бали) |
||||||
|
1. Вершини А і В трикутника АВС лежать по один бік від площин |
||||||
Рефлексія
На уроці я
• зрозумів…
• навчився…
• найбільший мій успіх…
• найбільші труднощі я відчував…
Домашнє завдання
№1. Точки A, B, C і D розташовані у просторі так, що продовження сторін AB і C D чотирикутника ABСD перетинаються. Довести , що вказані точки належать одній площині.
№2. Серед точок A, B, C і D ніякі три не лежать на одній прямій. Чи можуть ці точки лежати в одній площині?
Якщо ти пропустив урок
Задача 1.
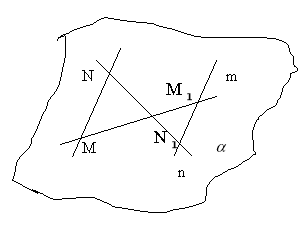 Дано дві прямі m і n, що перетинаються. Точки М і М
Дано дві прямі m і n, що перетинаються. Точки М і М![]() лежать на прямій m, а точки N i N
лежать на прямій m, а точки N i N![]() - на прямій n.До ведіть, що прямій MN i M
- на прямій n.До ведіть, що прямій MN i M![]() N
N![]() лежать в одній площині.
лежать в одній площині.
Картка – підказка
-
Прямі m і n визначають єдину площину
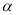 .(Поясніть чому.)
.(Поясніть чому.)
- В якій площині лежать точки М і N?
- В якій площині лежать точки M1 і N1?
- Де лежить пряма МN?
- В якій площині лежить пряма M1N1?
- Зробіть висновок.
|
Задача №2 Дано дві прямі m і n, що перетинаються. Точки М і М1 лежать на прямій m, а точки N i N1 - на прямій n. Доведіть, що прямі MN i M1N1 лежать в одній площині. Алгоритм розв’язання задачі 1. Проведіть та обґрунтуйте існування площини α. 2. Обґрунтуйте належність точок M1, N1, М і N площині α 3. Обґрунтуйте належність прямих M1N1 і МN площині α |
|
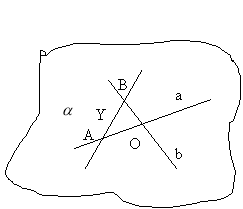
Прямі а та b перетинаються в точці О. А Картка-підказка
|
|
Задача №4
Прямі а та b перетинаються в точці О. А Алгоритм розв’язання задачі
|


про публікацію авторської розробки
Додати розробку