Організація самостійної діяльності учнів на уроках геометрії при вивченні теми "Аксіоми стереометрії" (2-й урок) для 10 класу
В процесі самостійного виконання різних вправ відбувається:
- закріплення математичних понять,
- формування та вдосконалення обчислювальних навичок, уміння застосовувати знання на практиці та використовувати свій досвід під час розв'язання задач,
- набування умінь геометричних побудов,
- розвиток прагнення обґрунтовувати висловлювання.
Урок № 1-5
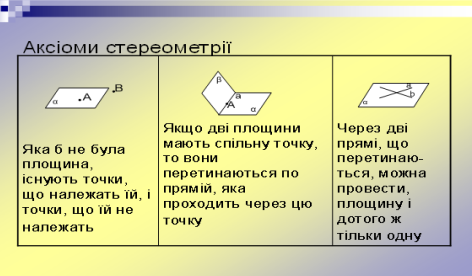
Тема: Аксіоми стереометрії
Актуалізація опорних знань через перевірку домашнього завдання
1. Учень нагадує суть доведення методом від супротивного
2. Виконання тестових завдань
Варiант 1
|
1) Яка з наведених фiгур не є основною фiгурою стереометрiї? |
|||
|
А) пряма |
Б) куля |
В) точка |
Г) площина |
|
2) Яке з наведених тверджень є аксіомою планіметрії ? |
|||
|
А) Сума сумiжних кутiв дорiвнює 180°.
|
Б) Яка б не була пряма, iснують точки, що належать цiй прямiй, i точки, що не належать їй.
|
В) Двi прямi на площинi називаються паралельними, якщо вони не перетинаються. |
Г) Через кожну точку прямої можна провести на площинi перпендикулярну до неї пряму i до того ж тiльки одну. |
|
3) Яке з наведених тверджень є теоремою планіметрії? |
|||
|
А) Вертикальнi кути рiвнi.
|
Б) Через будь-якi двi точки можна провести пряму i тiльки одну.
|
В) Кожний вiдрiзок має певну довжину, бiльшу вiд нуля.
|
Г) Трикутник називається рівнобедреним, якщо двi його сторони рiвнi. |
|
4) Яке з наведених тверджень правильне? |
|||
|
А) Через три точки завжди можна провести пряму i тiльки одну.
|
Б) Через три точки в жодному разi не можна провести прямої.
|
В) Через одну точку можна провести 1 000 000 прямих.
|
Г) На площинi не iснує iнших точок, крiм тих, що належать певнiй прямiй. |
Варiант 2
|
1) Яка з наведених фiгур не є основною фiгурою стереометрiї? |
|||
|
А) Площина |
Б) куб |
В) пряма |
Г) точка |
|
2) Яке з наведених тверджень є аксiомою планіметрії? |
|||
|
А) Яка б не була пряма, iснують точки, що належать цiй прямiй, i точки, що не належать їй. |
Б) У рівнобедреному трикутнику кути при основi рiвнi.
|
В) Вертикальнi кути рiвнi.
|
Г) Вiдрiзок, що сполучає двi точки кола, називається хордою.
|
|
3) Яке з наведених тверджень є теоремою шкiльного курсу геометрiї? |
|||
|
А) Паралелограм — це чотирикутник, у якого протилежнi сторони паралельнi.
|
Б) Сума кутiв трикутника дорiвнює 180°.
|
В) Довжина вiдрiзка дорiвнює сумi довжин частин, на якi вiн дiлиться будь-якою точкою.
|
Г) Через точку, що не лежить на прямiй, можна провести на площинi не бiльше однiєї прямої, паралельної поданiй. |
|
4) Яке з наведених тверджень правильне? |
|||
|
А) Через будь-якi двi точки можна провести пряму i до того ж не одну. |
Б) Яка б не була пряма, iснує 1 000 000 точок, що не належать їй. |
В) Із трьох точок на певнiй прямiй жодна не лежить мiж двома iншими |
Г) Довжина вiдрiзка не може дорівнювати 10-2 см. |
Вивчення нового матеріалу
Після пояснення викладачем нового матеріалу учні самостійно, використовуючи записи на дошці, складають опорний конспект
Контроль та корекція первісного сприйняття вивченого матеріалу
Самостійна робота за картками-завданнями
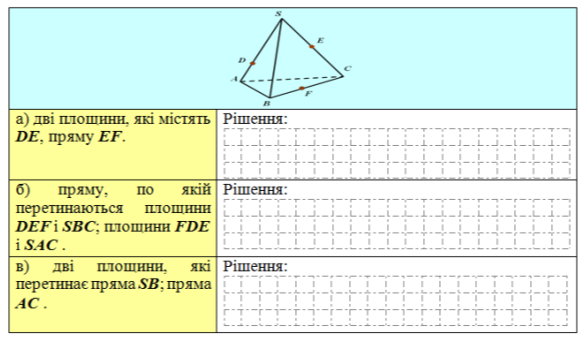
І варіант
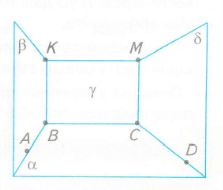
Користуючись даним малюнком назвіть:
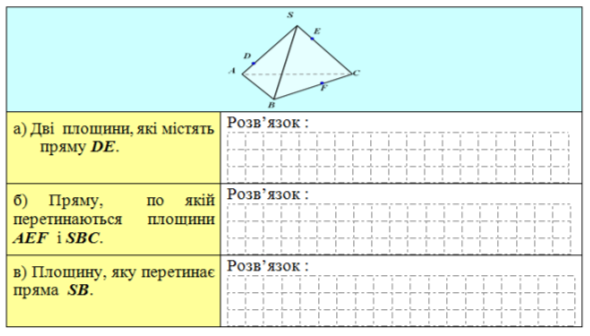
ІІ варіант
Рефлексія
На уроці я
• вивчив …
• зрозумів…
• навчився…
• я не знав, а тепер знаю …
• найбільші труднощі я відчував…
Домашнє завдання
Користуючись малюнком заповнити таблицю 
Якщо ти пропустив урок…
Задача.
Розв’язати, заповнивши пропуски
|
Умова |
Малюнок |
Розв’язування |
|
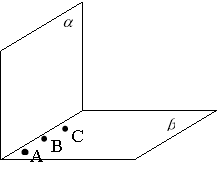
Точки А, В, С лежать у кожній з двох різних площин. Доведіть, що ці точки лежать на одній прямій.
|
|
Нехай дві різні площини |


про публікацію авторської розробки
Додати розробку