Організація самостійної діяльності учнів на уроках геометрії при вивченні теми "Наслідки аксіом стереометрії" для 10 класу
Побудова математики як цілісного учбового предмету – вельми складна задача, що вимагає додаткових сумісних зусиль викладачів, психологів, логіків, учнів і батьків. Тому велику увагу слід приділяти організації самостійної діяльності учнів, що сприяє розвитку їх пізнавальних здібностей.
Тема: Наслідки аксіом стереометрії
Перевірка домашнього завдання.
Актуалізація опорних знань
Гра «Геометричне лото»
Учні об'єднується у дві групи, отримують картки - «половинки» тверджень, та складають з них правильні твердження та формулюють їх.
|
I група |
II група |
|
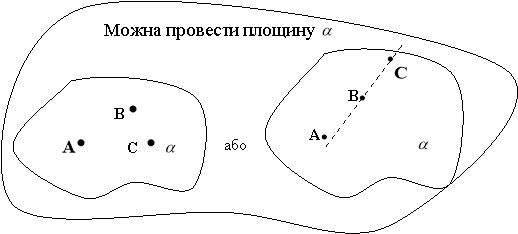
Через будь – які три точки, що не лежать на одній прямій… |
Якщо дві площини мають спільну точку… |
|
Якщо точки А, В і С лежать у кожній з двох різних площин, то… |
Через дві точки простору можна провести… |
|
… то вони перетинаються по прямій, яка проходить через цю точку |
… вони лежать на одній прямій |
|
… одну пряму, але безліч площин |
… можна провести площину, і до того ж тільки одну |
Вивчення нового матеріалу
|
Висновки |
Після вивчення другого наслідку з аксіом стереометрії (теореми про існування площини, що проходить через три точки) можна підвести учнів до висновків.
|
Способи задання площини:
|
![]()
![]()
|
Структура доведення теореми існування та єдності:
|
Первинне усвідомлення нового матеріалу
1. Самостійне виконання задачі за ланцюжком міркувань
Задача.
Доведіть, що через будь-які дві різні точки простору можна провести пряму, і до того ж тільки одну.
 Ланцюжок міркувань під час розв’язування задачі може бути таким:
Ланцюжок міркувань під час розв’язування задачі може бути таким:

![]()
![]()
![]()
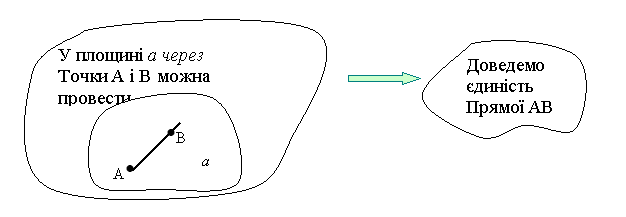
Зауваження. Необхідність доведення єдності прямої АВ випливає з довільності вибору точки С.
Розв’язання цієї задачі є дуже корисним тому, що:
- Застосовуються вивчені твердження;
- Застосовується необхідність доведення єдиності;
- Ще раз доводиться єдиність методом від супротивного.
- Математичний диктант
|
Які з наведених тверджень є правильними? |
|
|
1 |
Сторони кожного кута лежать в одній площині. |
|
2 |
Сторони кожного кута визначають єдину площину. |
|
3 |
Суміжні кути лежать в одній площині. |
|
4 |
Кожні три точки визначають єдину площину. |
|
5 |
Якщо дві різні площини мають спільну пряму, то, крім точок цієї прямої, у них немає спільних точок. |
|
6 |
Якщо дві різні площини мають спільні точки А і В, то вони перетинаються по прямій АВ. |
|
7 |
Через пряму і точку можна провести тільки одну площину. |
|
8 |
Три точки простору визначають єдину площину. |
Номери правильних відповідей учні записують на аркушах та здають викладачу (відповідь 1, 3, 5, 6)
Формування навичок застосування знань
Задачі учні розв’язують об’єднавшись у групи. Перевірка здійснюється у формі бліц-звітів за заздалегідь підготовленими рисунками.
№1. Дано чотири точки, що не лежать на одній прямій. Доведіть, що жодні три з них не лежать на одній прямій.
№2. Вершина С плоского чотирикутника АВСD лежить у площині ![]() . Прямі АВ і ADперетинають площину
. Прямі АВ і ADперетинають площину ![]() в точках В1 і D1 відповідно. Яке взаємне розташування точок С1, В1, D1? Відповідь обґрунтуйте.
в точках В1 і D1 відповідно. Яке взаємне розташування точок С1, В1, D1? Відповідь обґрунтуйте.
Контроль засвоєння теми уроків
Виконання тестових завдань
|
Варiант 1 |
|||
|
1) Скiльки площин можна провести через три точки? |
|||
|
А) Одну; |
Б) жодної; |
В) безлiч; |
Г) одну або безлiч. |
|
2) Через яку фiгуру можна провести бiльш нiж одну площину? |
|||
|
А) Пряму i точку на нiй;
|
Б) пряму i точку поза нею;
|
В) двi прямi, що мають спiльну точку; |
Г) три точки, що не належать однiй прямiй.
|
|
3) Продовжте речення: «Пряма обов’язково належить площинi, якщо...» |
|||
|
А) Вона має з площиною хоча б одну спiльну точку; |
Б) вона перетинає площину;
|
В) двi точки прямої належать площинi;
|
Г) жодна точка прямої не належить площинi.
|
|
4) На яке запитання треба дати позитивну вiдповiдь? |
|||
|
А) Чотири точки не лежать в однiй площинi. Чи можуть якi-небудь три з них лежати на однiй прямiй?
|
Б) Дано чотири точки, з яких жоднi три не лежать на однiй прямiй. Чи можуть цi чотири точки лежати в однiй площинi? |
В) Чи завжди можна провести тiльки одну площину через пряму i точку?
|
Г) Чи правильно, що якщо пряма перетинає кожну з двох прямих, якi перетинаються, то всi цi три прямi обов’язково лежать в однiй площинi?
|
|
Варiант 2 |
|||
|
1) Скiльки площин можна провести через пряму i точку? |
|||
|
А) Одну; |
Б) жодної; |
В) безлiч; |
Г) одну або безлiч. |
|
2) Через яку фiгуру можна провести тiльки одну площину? |
|||
|
А) Двi точки;
|
Б) пряму, на якiй позначено три точки; |
В) три точки, що не належать однiй прямiй |
Г) три прямi, що мають спiльну точку.
|
|
3) Продовжте речення: «Через будь-якi двi точки простору можна провести...» |
|||
|
А) площину, i тiльки одну; |
Б) пряму, i тiльки одну; |
В) безлiч прямих;
|
Г) жодної площини.
|
|
4) На яке запитання треба дати негативну вiдповiдь? |
|||
|
А) Чи правильно, що всi прямi, якi перетинають пряму i проходять через точку поза прямою, лежать в однiй площинi? |
Б) Чи правильно, що якщо через чотири точки можна провести площину, то обов’язково тiльки одну? |
В) Чи можна провести через пряму двi рiзнi площини?
|
Г) Чи правильно, що три прямi, якi проходять через одну точку, можуть не лежати в однiй площинi?
|
Рефлексія
На уроці я
• дізнався …
• зрозумів …
• навчився…
• найбільший мій успіх…
• найбільші труднощі я відчував…
• я не вмів, а тепер вмію …
Домашнє завдання
№1. Чи можна через точку перетину двох даних прямих провести третю пряму, яка не лежить з ними в одній площині? Відповідь поясніть.
№2*. Дано два відрізка що перетинаються: 1)AC і BD 2) AB і CD. Чи лежать в одній площині прямі BA, DC, DB і CA? Відповідь поясніть.
Якщо ти пропустив урок
|
Наслідок 1 |
Наслідок 2 |
|
|
|
|
Через пряму і точку, яка не лежить на ній,можна провести площину і до того ж тільки одну. |
Через дві прямі, що перетинаються, можна провести площину і до того ж тільки одну |
Зразки розв’язування задач
Задача 1.
|
Чи можна через точку перетину двох даних прямих провести третю пряму, яка б не лежала з ними в одній площині? |
||
|
Розв’язання |
Малюнок |
Чому саме так? |
|
Відповідь: Можна. |
|
Очевидно, що точки площини задаватимуть прямі, які будуть належати цій самій площині. Якщо ж взяти точку перетину двох прямих на площині та точку поза площиною, то через будь-які дві точки простору можна провести пряму. Ця пряма матиме лише одну спільну точку з площиною, а значить, буде її перетинати. |
Задача 2.
|
Доведіть, що всі прямі, які перетинають дві дані паралельні прямі, лежать в одній площині. |
|
Доведення
Оскільки пряма a i b паралельні, то,за означенням, ці прямі лежать в одній площині a. Довільна пряма с, яка перетинає a i b, має з площиною a дві спільні точки – точки перетину. Згідно з теоремою 2, ця пряма належить площині a. Отже, всі прямі, які перетинають дві паралельні прямі, лежать в одній площині, що й вимагалося довести. |
Задача 3.
|
Доведіть, що коли прямі AB i CD не лежать в одній площині, то прямі AC i BD теж не лежать в одній площині. |
|
|
Доведення |
Чому саме так? |
|
Доведемо методом від супротивного. Припустимо, що прямі AC i BD лежать в одній площині. Тоді точки А, В , С, D належать цій площині, а тому прямі AB i CD належать цій площині, що суперечать умові. Припущення неправильне, тому прямі AC i BD не належать одній площині, що й вимагалося довести. |
Під час доведення належності чи не належності часто використовують метод доведення від супротивного. У цьому випадку він одразу виводить на суперечність, а значить – доводить вимогу задачі. |


про публікацію авторської розробки
Додати розробку