Організація самостійної діяльності учнів на уроках геометрії при вивченні теми "Аксіоми стереометрії" для 10 класу

Тема: Основні поняття стереометрії

Актуалізація опорних знань

 1. Фронтальне повторення аксіом планіметрії

 2. Математичний диктант

1. Які основні фігури на площині ви знаєте?
2. Як позначаються точка, пряма?
3. Наведіть приклади інших фігур на площині.
4. Що таке аксіома.

5. Дайте означення теореми.

6. Наведіть приклад будь-якої теореми.

       Перевірка математичного диктанту проводиться за допомогою взаємоперевірки, учні міняються зошитами, слухають правильну відповідь та ставлять «+» або «-».

 

Мовативація

       Перегляд учнівської презентації на тему «Просторові фігури» (випереджаюче креативне домашнє завдання)

 

Вивчення нового матеріалу

        Під час пояснення викладачем матеріалу учні самостійно складають опорний конспект

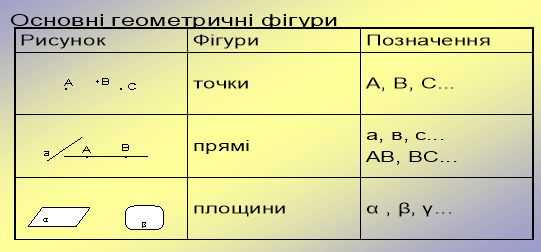
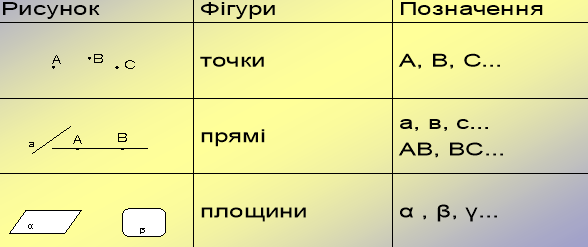«Основні геометричні фігури»

 

та заповнюють схему

«Логiчна будова геометрії»

 

 

 

 

 

 

 

 

 

 

 

 

 Первісне закріплення матеріалу

Вправи на розвинення просторових уявлень

№1. На рисунку зображено одну й ту саму фiгуру, але в рiзних положеннях. Де повинна стояти «зiрочка» у кожнiй iз фiгур?

 

№2. Куб iз ребром 5 см пофарбували в зелений колір. Потiм його розрізали на маленькі кубики, ребро кожного з яких дорівнює 1 см. Скiльки кубикiв мають:

а) одну зафарбовану грань;                   б) дві зафарбованi гранi;

в) три зафарбованi гранi;                       г) жодної зафарбованої гранi?

 

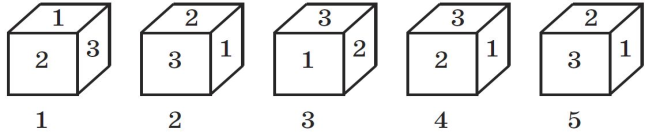№3.  Якi з кубикiв вiдрiзняються вiд першого тiльки розмiщенням у просторi?

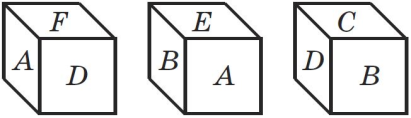
№4. На гранях куба написанi букви A, B, C, D, E, F. Визначте, якi букви написанi на протилежних гранях куба за його рисунками в трьох положеннях у просторi.

 

 

 

 

Підсумок уроку

1. Завдання

Побудуйте та запишіть за допомогою символів:

а) площину α і точку А, що лежить у ній;

б) площину α і точку В, яка не лежить у ній;

в) площину β, яка проходить через пряму а;

г) площину γ та пряму а, яка не лежить у площині γ;

д) дві площини α і β,  які проходять через пряму с.

 

     2. Рефлексія :

• Яку мету Ви ставили перед собою на початку уроку?
• Чи досягли Ви цю мету?
• Що нового Ви узнали на уроці?
• Що Вам запам’яталося на уроці?

 

Домашнє завдання

№1. Які з наведених фігур є основними в стереометрії:

1) точка;  2) відрізок;  3) промінь

4) пряма; 5) кут;           6) трикутник;

7) коло;  8) ромб;           9) куб

10) куля; 11) площина; 12) призма?

№2. Повторити метод доведення від супротивного.

 

 

Якщо ти пропустив урок…

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задача 1. Площини α та  β перетинаються по прямій b. Пряма а лежить у площині α та перетинає площину β у точці М. Доведіть, що точка М лежить на прямій b.              

Підказка до рішення задачі

Заповніть пропуски:

1) М α, М а,  α ∩ β = b (за умовою)

2) Тоді, М … (якій площині?).

3) Отже, М – спільна точка … (яких площин?);

4) А значить, М b (чому ? за якою аксіомою?)

 

Задача 2. Доведіть, що через пряму і точку, яка їй не належить, можна провести площину.

Розібрати розв’язування задачі за зразком