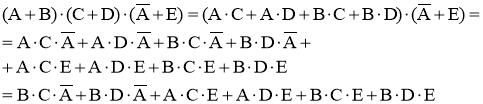Організаційно-методичні аспекти навчання стохастики в дев'ятих класах із поглибленим вивченням математики

ЗМІСТ

Стор.

ВСТУП

Актуальність дослідження. Стохастичні процеси притаманні усім галузям людської діяльності, і, звичайно, економічній. Методи теорії ймовірностей та математичної статистики (стохастики) поряд з іншими стали потужним інструментом дослідження сучасної економіки, вони широко використовуються при вивченні і прогнозуванні економічних явищ і процесів, пов’язаних з роздержавленням власності, розгортанням процесу приватизації, вдосконаленням ринкових відносин тощо.

Вивчення математики в сучасних умовах набуває особливої актуальності. Зумовлено це тим, що все більше спеціальностей потребують застосувань математичних знань, практичних навичок і умінь високого рівня. Сучасні трасформації національної школи України включають в себе удосконалення математичної освіти, основними напрямками якої є оновлення змісту і технології навчання математики. Особистісно орієнтоване навчання, рівнева і профільна диференціація, які ґрунтуються на розробках стандартів математичної освіти, є основою для створення умов досягнення кожним учнем оптимального для нього рівня математичних знань і умінь, загального та математичного розвитку.

Сучасне і, насамперед, майбутнє суспільство вимагає від працівників знань основ математичного аналізу, математичної логіки, теорії ймовірностей, інформатики, статистики.

Учні, які зацікавлені математикою, можуть одержати сучасну підвищену та поглиблену підготовку у класах з поглибленим її вивченням та в школах нового типу, де передбачається високий рівень математичної підготовки для здібних та обдарованих дітей (гімназіях, ліцеях, профільних класах різного спрямування), які набули останнім часом поширення в Україні. Ефективну діяльність таких шкіл і класів можна забезпечувати лише за умови розробки відповідної методичної системи навчання, зокрема,  уточнення цілі, завдань і змісту навчання;  наявності сучасних підручників для учнів і методичних посібників для вчителів з математики та інформаційних технологій.

Проблема ймовірнісно-статистичної освіти учнівства є актуальною, але не є новою в теорії та практиці шкільної математичної освіти. Вона має понад сторічну історію і над її розв’язанням працювали видатні вітчизняні та зарубіжні вчені: В.Я.Буняковський, Б.В.Гнєденко, В.П.Єрмаков, А.М.Колмогоров, А.Реньї, В.Г.Розумовський, М.М.Філіпов, С.П.Фролов та ін.

Одна із актуальних на сьогодні проблем полягає в тому, щоб, враховуючи сучасний розвиток математики та методики навчання математики, розкрити  можливості ефективної реалізації ї математичної підготовки учнів 9-х з поглибленим вивченням математики в процесі вивчення елементів стохастики, розвитку їхніх математичних здібностей. Вище названі чинники зумовили вибір теми нашого дослідження «Організаційно-методичні аспекти вивчення елементів стохастики в 9-х класах з поглибленим вивченням математики».

Об’єктом дослідження є процес вивчення елементів стохастики в 9-х класах з поглибленим вивченням математики.

Предметом дослідження є окремі компоненти методичної системи вивчення елементів стохастики в 9-х класах з поглибленим вивченням математики.

Мета дослідження полягає у розробці та теоретичному обґрунтуванні доцільності впровадження методики навчання стохастики в дев’ятих класах із поглибленим вивченням математики.

Гіпотеза дослідження. Якщо уточнити цілі,  завдання та зміст, розробити ефективні форми, методи і засоби вивчення елементів стохастики в 9-х класах з поглибленим вивченням математики, орієнтовані на розв'язання прикладних задач, враховуючи сучасні технології навчання та інформаційні технології, то можна забезпечити той рівень математичної підготовки із зазначених тем, який вимагається нормативними документами.

Мета і предмет та висунута гіпотеза дозволили визначити основні завдання дослідження:

1) проаналізувати психолого-педагогічну, навчальну, математичну і методичну літературу, яка має відношення до проблеми дослідження та вивчити сучасний стан навчання  елементів стохастики в 9-х класах з поглибленим вивченням математики;

2) виявити психолого-педагогічні передумови та методичні вимоги до структури змісту теоретичного матеріалу та системи задач із стохастики в 9-х класах з поглибленим вивченням математики;

 3) розробити компоненти методичної системи навчання елементів стохастики в 9-х класах з поглибленим вивченням математики;

4) експериментально перевірити ефективність розробленої методичної системи та внести необхідні корективи в методичні рекомендації.

Для досягнення мети і розв’язання поставлених завдань були використані такі науково-педагогічні методи  дослідження:

теоретичні: системний і порівняльний аналіз психолого-педагогічної і науково-методичної літератури з проблем дослідження; порівняння, узагальнення  і систематизація науково-теоретичних положень; моделювання педагогічних процесів, обробка результатів педагогічного експерименту методами математичної статистики.

емпіричні: діагностичні (бесіди з учителями, учнями та вчителями), обсерваційні (спостереження навчального процесу у класах з поглибленим вивченням математики, аналіз уроків, письмових робіт учнів, узагальнення передового педагогічного досвіду); експериментальний (організація і проведення констатуючого і формуючого експерименту).

Наукова новизна дослідження полягає в теоретичному і експериментальному обґрунтуванні методики вивчення елементів стохастики в 9-х класах з поглибленим вивченням математики, яка забезпечує формування стохастичного мислення учнів через моделювання стохастичних явищ, в основі яких лежать стохастичні задачі прикладного змісту.

Теоретичне значення дослідження полягає у виділенні психолого-педагогічних і методичних передумов, уточненні змісту навчання, визначенні цілей і завдань, доборі методів, організаційних форм та засобів, навчання та контролю успішності учнів, що сприяють поглибленому вивченню вивчення елементів стохастики в 9-х класах з поглибленим вивченням математики.

Практична значимість результатів дослідження визначається тим, що:

• впровадження в практику розробленої методичної системи вивчення елементів стохастики в 9-х класах з поглибленим вивченням математики буде сприяти підвищенню ефективності вивчення нової змістової лінії і шкільної математики в цілому, загальному та математичному розвитку учнів;
• підготовлені методичні рекомендації та дидактичні матеріали  допоможуть організувати на належному рівні вивчення теоретичного матеріалу і процес формування вмінь розв’язувати ймовірнісні задачі, в тому числі і прикладного змісту;
• розроблені  дидактичні матеріали забезпечать організацію контролю рівня успішності та математичного розвитку учнів 9-х класах з поглибленим вивченням математики.

Обсяг та структура роботи. Дипломна робота складається із вступу, двох розділів, висновків, списку використаних джерел 50.  Загальний обсяг роботи 75 сторінок. У першому розділі ми звернемо увагу на психолого-педагогічні передумови та методичні вимоги до структури змісту теоретичного матеріалу та системи задач із стохастики в 9-х класах з поглибленим вивченням математики, а в другому – на створення педагогічних умов вивчення елементів стохастики в 9-х класах з поглибленим вивченням математики; експериментальну перевірку ефективності розробленої методичної системи.

РОЗДІЛ  I РОЗВИТОК ЙМОВІРНО-СТАТИСТИЧНОЇ ЛІНІЇ В ТЕОРІЇ І ПРАКТИЦІЇ СУЧАСНОЇ ШКОЛИ

1.           Місце і роль теорії ймовірностей на уроках математики

Математична освіта є важливою складовою загальноосвітньої підготовки учнів. Місце математики в системі шкільної освіти визначається її роллю в інтелектуальному, соціальному та моральному розвитку особистості, розумінні будови і використання сучасної техніки, нових інформаційних технологій, сприйманні наукових і технічних ідей, формуванні наукової картини світу і сучасного світогляду.

Математика є опорним предметом при вивченні суміжних дисциплін, таких як: фізика, хімія, інформатика, біологія, географія, економіка, креслення. Зазначені дисципліни користуються математичними принципами і методами для розв’язання профільних задач, яке зводиться до абстрагування та побудови математичної моделі.

На сьогодні, зміст навчального матеріалу має забезпечувати не екстенсивне, а інтенсивне навчання і самонавчання учнів, перенесення акцентів із збільшення обсягу інформації, призначеної для засвоєння учнями, на вироблення вмінь її використовувати для досягнення конкретних цілей, тобто на інтелектуальний розвиток учня.

Знати математику – це вміти її застосовувати. Цей підхід передбачає не лише засвоєння готових знань, а й способів міркувань, що застосовуються в математиці, створення педагогічних ситуацій, що стимулюють самостійні відкриття учнями математичних фактів. З огляду на це навчальний матеріал повинен містити загальні схеми розв’язування задач, загальні підходи до моделювання прикладних ситуацій, відомості про суть задачі, їх склад і структуру [17].

Модернізація шкільного курсу математики за рахунок введення курсу початків теорії ймовірностей та елементів математичної статистики, безумовно, відіграє позитивну роль у посиленні його прикладної спрямованості.

Сфера застосувань теорії ймовірностей надзвичайно широка. Теорія ймовірностей вивчає всі масові явища, тобто випадки, що часто повторюються в будь-якій галузі життя, науки або техніки.

Останнім часом теорія ймовірностей набула важливого застосування в астрономії. Особливо, коли астрономи почали вивчати не лише окремі планети та зірки, а й цілі маси зірок – зоряні скупчення, а також позагалактичні туманності, або галактики, що складаються з величезної кількості окремих зірок. В астрономії почав розвиватися напрям, що вивчає методами теорії ймовірностей усю масу галактики, подібних до тієї величезної зоряної системи, до якої належить наше Сонце з усіма планетами.

Висновки теорії ймовірностей можна застосувати до фізичних явищ. У другій половині XIX ст. у працях англійця К. Максвелла, австрійця Л. Больцмана та американця Д.В.Гіббса зародилася така звана статистична фізика – галузь фізики, що вивчає величезні сукупності атомів чи молекул, з яких складається речовина.

Звільнення атомної енергії поставило нові серйозні завдання перед теорією ймовірностей. У будь-якій атомній установці основну роль відіграють ядерні реакції – процеси поділу або зміни атомних ядер, спричинювані їх випадковими зіткненнями з найдрібнішими елементарними частинками і однієї з одною. При цьому дуже важливо заздалегідь розрахувати хід усіх процесів в установці – найменша помилка може бути причиною грандіозної катастрофи. І тут на допомогу приходить теорія ймовірностей: незважаючи на випадковий характер окремих атомних зіткнень, вона дає змогу з великою точністю визначити, як відбуватимуться зміни в усій масі атомів [22].

Кожен з нас користується телефоном. Можливість обладнання телефонних автоматичних станцій обґрунтована теорією ймовірностей. Розглянемо такий приклад. Теорія ймовірності дала змогу розрахувати приблизну кількість людей, які одночасно звертаються до авто довідки служби часу. І хоч таких людей в місті дуже багато, авто довідка ніколи не буває зайнята. Це пояснюється тим, що теорія ймовірностей дає змогу зробити розрахунок, скільки людей і в який час звертатимуться за довідкою. Виходячи з цього, можна визначити мінімальну кількість комплектів автоматичних апаратів, потрібну для того, щоб задовольнити потреби мільйонів жителів міста.

Практичне значення теорії ймовірностей зростає з кожним роком. Саме ця обставина зумовлює необхідність вивчення елементів теорії ймовірностей в плані загальної математичної освіти.

Вивчення різних розділів курсу математики, має бути диференційованим. Це забезпечується відмінністю цілей, змісту, методики навчання різних категорій учнів. У процесі поглибленого вивчення математики основні завдання суттєво доповнюються. Математична освіта в профільних класах, повинна мати таку структуру: основний курс математики система спецкурсів або курсів за вибором, індивідуальна робота творчого характеру з учнями.

Вивчення питань з теорії ймовірностей в класах з поглибленим вивченням математики за навчальними програмами, які пропонує Міністерство освіти і науки України починається в восьмому класі. Для вивчення розділу «Множини. Елементи математичної логіки. Комбінаторика. Імовірність.» Відводиться 12 – 17 годин. До учнів ставляться такі вимоги: мати уявлення про теорію ймовірностей, як науку, подію, випадкову подію та статистичну ймовірність випадкової події та вміти розв’язувати найпростіші задачі на обчислення статистичних ймовірностей.

В дев’ятому класі з розділу «Множини. Комбінаторика. Імовірність.» (17 – 20 годин) вивчаються такі теми: «Випадкові події» та «Обчислення статистичних ймовірностей випадкових подій».

Основне вивчення початків теорії ймовірностей відбувається в одинадцятому класі.

Відповідно до Типових навчальних планів загальноосвітніх навчальних закладів, затверджених наказом Міністерства освіти і науки України, на вивчення теми «Початки теорії ймовірностей» у класах з поглибленим вивченням математики відводиться 25 годин у другому семестрі одинадцятого класу.

На рівні обов’язкових результатів навчання проект освітнього стандарту з математики для середньої школи передбачив такий зміст навчального матеріалу.

Початки теорії ймовірностей.

І. Предмет і методи теорії ймовірностей. Стохастичний експеримент. Елементарна подія. Множина елементарних подій. Операції над подіями, сума, добуток, різниця подій. Протилежна подія. Геометрична інтерпретація операцій над подіями.

ІІ. Поняття ймовірності випадкової події. Означення ймовірності. Дискретні і недискретні розподіли ймовірностей. Обчислення ймовірностей випадкових подій. Поняття про центр розподілу ймовірностей.

ІІІ. Умовні ймовірності. Залежні і незалежні події. Ймовірність добутку і суми подій. Повторні незалежні випробування. Формула Бернулі. Закон великих чисел [25].

Основна мета викладання зазначених тем – сформувати уявлення про основні поняття теорії ймовірностей та виробити вміння застосовувати їх до розв’язування простих задач.

Методичні підходи та організаційні форми навчання добираються вчителем відповідно до вікових особливостей учнів та змісту навчального матеріалу. Багаторічний досвід функціонування в Україні класів з поглибленим вивченням математики переконує в тому, що недоцільно надмірно заповнювати програму додатковими питаннями. Це спричиняє навантаження і, як наслідок відсів учнів. Розвитку стійких пізнавальних математичних інтересів сприяють дібрані в системі різноманітні складні задачі з достатнім евристичним навантаженням та пов’язаний з темою історичний матеріал.

До арсеналу засобів навчання повинні увійти дидактичні ігри та експерименти, живі спостереження та предметна діяльність учнів, зокрема лабораторні роботи з теорії ймовірностей та математичної статистики.

Лабораторні роботи повинні мати приблизно такий зміст:

Розглядається деяка ситуація, наслідки якої залежать від випадкових обставин і які не можна передбачити. Необхідно побудувати її імовірнісну модель. У межах цієї моделі пропонується знайти ймовірність деяких подій, побудувати закони розподілу кількох випадкових величин, обчислити їхні числові характеристики. Далі передбачається виконати експеримент, який моделював би ситуацію, що розглядається. За результатами цього експерименту обчислюються вибіркові середні для випадкових величин, що розглядались, та відносні частоти тих подій, про які йшлося. Ці характеристики порівнюються з відповідними теоретичними даними (звісно, їх необхідно розрахувати). Будуються графіки залежності вибіркових середніх та відносних частот від кількості дослідів.

Виконання таких робіт сприяє формуванню поняття стійкості у світі випадкового.

Поява імовірнісно-статистичної лінії в школі породила чимало проблем, неготовими виявились майже всі – від вчителів до авторів шкільних підручників. Дивно, але маючи одну з найбільш відомих і визнаних в усьому світі академічних шкіл теорії ймовірностей, ми досі не маємо загальної концепції викладання цього розділу математики у школі, ні достатньої кількості навчальних посібників для школярів, які б містили відповідний матеріал.

Розв’язання елементарних задач на обчислення ймовірності потребує наявності розвинутого імовірнісного мислення, а закласти основи такого мислення можна лише в школі. Змінюється концепція курсу для школи. Якщо в вищій школі основний акцент робиться на вивчення математичного апарату для аналізу імовірнісних моделей, то в школі учнів передусім необхідно ознайомити з процесом побудови моделі, вчити їх аналізувати, перевіряти адекватність побудованої моделі реальним ситуаціям, розвивати імовірнісну інтуїцію.

На шляху введення імовірнісно-статистичної лінії в шкільний курс математики потрібно зробити наступні кроки. По-перше, необхідно якомога раніше починати цілеспрямовано формувати й розвивати імовірнісно-статистичний тип мислення, неперервно нарощуючи обсяг та зміст навчального матеріалу, підвищуючи його рівень. По-друге, ця лінія повинна знаходитись у природному зв’язку з традиційним шкільним курсом математики. По-третє, слід забезпечити застосування імовірнісних знань в інших предметах. Знання та навички, набуті при вивченні ймовірності та статистики, повинні знайти застосування на уроках фізики, хімії, біології при оформленні лабораторних робіт, результатів спостережень і дослідів, на уроках географії, історії для сприйняття інформації, яка подана в табличній, або графічній формах.

Необхідною умовою успішного введення розділу «Теорія ймовірностей» в зміст шкільної математичної освіти є розробка якісного навчально-методичного забезпечення. Воно має бути традиційним для курсу математики і містити підручник (або розділи підручника), збірник задач, дидактичні матеріали, збірник тестів, посібник для вчителя. Але нова змістова лінія передбачає своєрідні форми, засоби та прийоми навчання. До арсеналу засобів навчання повинні увійти дидактичні ігри та експерименти, живі спостереження та предметна діяльність учнів, зокрема лабораторні роботи.

Успіх втілення нової змістової лінії в шкільний курс математики значною мірою залежить від всебічної готовності вчителя до цієї роботи: психологічної, математичної, методичної. Вчителю необхідно подолати такі труднощі, що постануть на його шляху:

1) ретельний добір змісту курсу;

2) кардинальне подсилення його прикладної спрямованості;

3) природне включення до курсу методичного наповнення;

4) застосування матеріалу, що вивчається, до розв’язання проблем суміжних дисциплін [26].

Однією з проблем вивчення початків теорії ймовірності є недостатність навчальної літератури, серед існуючих навчальних посібників лише деякі містять необхідний теоретичний та практичний матеріал з теми.

Основний підручник, який на сьогодні використовується в загальноосвітніх школах для вивчення математики в одинадцятих класах це – Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу 11 клас. Теоретичний матеріал подано в необхідному для рівня обов’язкових результатів навчання мінімумі. Текст супроводжується малюнками, наводяться приклади. Для практичної роботи учнів представлена добірка завдань, але задач недостатньо для того, щоб використати і для роботи на уроці, і для домашніх завдань і для перевірки рівня знань, вмінь та навичок.

Повно та змістовно розкрито зміст теоретичних питань з теорії ймовірностей в посібнику для вчителів М.І. Жалдака та Г.О. Михаліна «Елементи стохастики з комп’ютерною підтримкою». Задач, наведених в кожному пункті посібника, небагато, вони, як правило, двох типів. Перший тип спрямовано на засвоєння теоретичного матеріалу та на розвиток логічного мислення. Більшість цих задач можна розв'язувати усно. Задачі другого типу частіше технічного характеру. В більшості задач не потрібно будувати математичну модель, вони абстраговані, тому мають непривабливий вигляд для школярів.

Імовірнісні задачі мають корисні для педагога-практика особливості. У переважній більшості випадків їх можні сформулювати на дуже вузькій понятійній базі. Більш того, значну їх кількість можна подати у привабливому для учнів сюжетному оформленні. Навіть найабстрактніші і найскладніші з них, як правило, піддаються адаптації для школярів.

Отже, на першому місці має бути евристична задача, яка одна лише спроможна будити думку, обіцяти винагороду, плекати інтелект. Коли учень здолає навіть одну таку задачу із кількох десятків – це буде незрівнянно вартісніший для нього здобуток, ніж сто докучливих рецептурних вправ із ста. Які якості можуть виховувати у кращому разі алгоритмічні вправи? Терпіння, уважність, покірливість, почуття безнадійної приреченості: роби, що кажуть, і як кажуть. Натомість справжня математична діяльність – а такою є тільки розв’язування евристичних задач – виховує спостережливість, силу волі (не опускати руки коли задача вперто не піддається), мужність (відмовитись від помилкової гіпотези чи ідеї, яка не виправдала сподівань), вміння перевіряти й обґрунтовувати гіпотези та будувати доказові міркування, нарешті ініціативність та почуття прекрасного.

Імовірнісні задачі не є алгоритмічними. Усім їм притаманна об‘єктивна або, щонайменше, психологічна дистанційованість від алгоритмічних схем. Вони мають також низку інших позитивних дидактичних властивостей: чітке психологічно прийнятне для дітей формулювання, широкі можливості для експериментування, узагальнень та спеціалізацій, практично не обмежені можливості для дитячої задачної творчості, до того ж не примітивно-шаблонної, висока пізнавальна та естетична якість розв’язків. Імовірнісні задачі просто-таки просяться у шкільний курс.

2.          Теоретичні основи введення ймовірнісно-статистичної лінії в шкільний курс математики

Мета навчання стохастики була сформульована, ще Б.В. Гнєденко і  полягає в ідейному збагаченні поглибленого курсу математики і підсиленню його розвиваючого і прикладного потенціалу, формуванні стохастичного мислення.

На сучасному етапі шкільної математичної освіти основними цілями навчання початків теорії ймовірностей і вступу до статистики є:

1.               забезпечення свідомого і міцного оволодіння знаннями, навичками і уміннями з даної змістової лінії, які потрібні в повсякденному житті, майбутній професійній діяльності і яких буде достатньо для вивчення інших предметів, продовження освіти, формування навичок моделювання випадкових явищ під час досліджень природи і суспільства;
2.               розвиток імовірнісно-статистичного мислення учнів, математичної інтуїції і культури, формування самостійності, ініціативності, творчості, здатності адаптування до умов, що змінюються;
3.               формування наукового світогляду, поваги до національної культури і традицій України, позитивних рис характеру, доброзичливості, толерантності, сміливості, обґрунтованості суджень, економічне, екологічне, трудове виховання, професійна орієнтація.

Імовірнісно-статистична змістовно-методична лінія повинна ґрунтуватися на принципах: 1) прикладної спрямованості; 2)  інтегрованості; 3)  між- предметних зв'язків; 4)  довготривалості; 5)  диференціації.

Змістово-методична лінія містить: імовірнісну і статистичну складові, які органічно доповнюють одна одну. Їх взаємозв’язок  забезпечує системність уявлень про роль емпіричних засобів і теоретичних методів у пізнанні явищ навколишнього світу і їх імовірнісної структури.

Сучасний етап навчання початкам теорії ймовірностей і вступу до статистики характеризується такими протиріччями:

1. програми для шкіл і класів з поглибленим вивченням математики не в повній мірі відповідають сучасним вимогам суспільства і потребам особистості учнів, тоді як володіння ними необхідне кожному учаснику виробничого процесу і суспільного життя;
2. обсяг і рівень складності навчального матеріалу з початків теорії ймовірностей і вступу до статистики для ліцеїв і класів з поглибленим вивченням математики є завищеним по відношенню до рівня,  необхідного при поглибленому навчанні. Надмірний обсяг і невиправдана складність перешкоджає розумінню і розвивають в учнів невіру у свої сили;
3. існує наявний розрив між знаннями, навичками і вміннями учнів: процес формалізації практичної задачі, пов’язаної з випадковим явищем, викликає великі труднощі навіть при наявності теоретичних знань;
4. більшість учнів не можуть розв’язувати навіть прості ймовірнісні задачі, оскільки нечітко уявляють, що таке випадкова подія, елементарна випадкова подія. Дуже часто плутають поняття незалежність і несумісність випадкових подій. А це в свою чергу призводить до неправильного використання теорем додавання і множення ймовірностей;
5. учні іноді не можуть відрізняти імовірність перетину випадкових подій від умовної ймовірності;
6. не завжди правильно розуміють імовірнісний зміст числових характеристик випадкових величин, не говорячи про економічний, технічний [23].

Для глибокого і правильного розуміння основних положень теорії ймовірності необхідно чітке розуміння  змісту початкових фундаментальних понять учнями, потрібен постійний зв’язок  теорії з практикою.

Етапи формування стохастичних уявлень, знань і умінь учнів, які мають здібності до математики, полягають у: знайомстві з найпростішими стохастичними ситуаціями; накопиченні систематизованих уявлень про явища стохастичної природи; створенні науково-технічної основи стохастичних уявлень.

Сформульовані методичні вимоги до навчання елементів стохастики в ліцеях і класах з поглибленим вивченням математики:

1. чітке визначення цілей і завдань навчання нової змістової лінії у зазначених класах;
2. зміст повинен забезпечувати наявність системи теоретичних імовірнісно-статистичних знань, відображати сучасний стан розвитку науки і техніки;
3. забезпечення формування міцних навичок і вмінь при  розв’язуванні стохастичних задач;
4. спрямування на встановлення тісного зв’язку ймовірнісних моделей з предметним світом, організацію побудови і тлумачення моделей як провідних форм діяльності учнів;
5. навчання повинно бути націленим на використання творчих можливостей  школярів як послідовності самостійних „відкриттів”, тобто повинно мати евристичний характер;
6. у навчанні повинні встановлюватися і реалізовуватися міжпредметні зв’язки в якості взаємодії між шкільними дисциплінами;
7.  навчання повинно здійснюватись на основі профільної і рівневої диференціації;
8. поряд з традиційними засобами навчання мають набути широкого використання засоби іформаційно-комунікаційних технологій  [19].

Основними складовими взаємозв’язків наступності у процесі навчання початкам теорії ймовірностей і вступу до статистики є: пропедевтика і наступність; наступність і повторення; наступність і міжпредметні зв’язки; наступність і перевивчення.

При розгляді питання методики структурування теоретичного матеріалу в умовах диференціації передбачається тісний взаємозв’язок з класичними галузями математики, що описують детерміновані явища, сприяють розкриттю потенціалу стохастики для підсилення внутрішньо предметних і міжпредметних зв’язків, допомагають усвідомити нові можливості шкільної  математики у пізнанні існуючих у дійсності взаємозв’язків і взаємозалежностей.

Вибір стилю подання початків теорії ймовірностей і вступу до статистики в класах різних профілів є досить істотним. Тут треба йти шляхом розумного компромісу між строгістю, доступністю й прикладною спрямованістю, не забуваючи  про жодну. 

У математичних класах виклад матеріалу носить досить абстрактний характер з високим ступенем формальних доведень, залишаючи більшу частину матеріалу, що вивчається, для самостійної роботи. Більшу ефективність дає лекційна форма роботи з наступними семінарськими заняттями.

У роботі використовується емпіричний підхід до формування поняття ймовірності, це дає змогу сформувати в учнів інтуїтивне уявлення не тільки  про ймовірність, а й про сучасний, тобто (аксіоматичний), метод побудови теорії ймовірностей. Поняття статистичної ймовірності  (відносної частоти) значно легше сприймається учнями з врахуванням їхніх вікових особливостей, бази математичних знань, життєвого досвіду, сформованості абстрактного мислення, здатності до узагальнень. Тому, формування основних понять теорії ймовірностей та математичної статистики природно починати з вивчення поняття статистичної ймовірності  та її властивостей.

При навчанні початків теорії ймовірностей і вступу до статистики доцільно використовувати ППЗ GRAN1, Microsoft EXEL.

Система задач, призначених для вивчення початків теорії ймовірностей і вступу до статистики, поряд з традиційними типами задач, включає задачі, які відсутні у діючих шкільних підручниках, але мають важливе значення в процесі вивчення даної змістової лінії. Тематика традиційних типів задач повинна бути розширена, фабула переважної більшості вдосконалена.

При вивченні початків теорії ймовірностей і вступу до статистики, як і при вивченні будь-якої змістової лінії алгебри і початків аналізу, найбільші труднощі викликає використання теорії для розв’язання практичних і прикладних задач.

При розробці методики формування імовірнісно-статистичного мислення учнів у процесі розв’язання задач з початків теорії ймовірностей і вступу до статистики необхідно вказати, що однією з основних проблем при цьому є відбір до кожної теми відповідних видів задач, які найбільш доречні з точки зору формування стохастичного мислення, формування відповідних умінь і, разом з тим,  доступних учням.

Система задач при навчанні початкам теорії ймовірностей і вступу до статистики повинна бути побудована за такими принципами: доступності, прикладної спрямованості і міжпредметних зв’язків, різноманітності, диференціації навчання, повторення та послідовного наростання труднощів, реалізації контролюючої функції, відповідності наявності часу, експериментально-дослідницький [18].

Система поточного і тематичного контролю, система індивідуальних задач, диференційованих за рівнями, дає змогу контролювати і закріпляти отримані знання, навички і вміння з початків теорії ймовірностей і вступу до статистики.

Індивідуалізація самостійних і домашніх завдань з обов’язковою подальшою перевіркою дозволить прищепити навички самостійної роботи, а індивідуальний практикум з розв’язання стохастичних задач сприятиме відпрацюванню певних умінь використання імовірнісно-статистичних понять і методів у школі.

Підсумовуючи вищевикладене, зазначимо, що ретроспективний аналіз розвитку шкільного курсу математики показав, що пропозиції щодо введення в шкільну програму початків теорії ймовірностей і вступу до статистики висувалися ще в кінці ХІХ століття видатними математиками і відомими діячами системи математичної освіти. Серед математиків ця пропозиція висувалася в Україні, зокрема, М.В.Остроградським  і професором В.П.Єрмаковим.

З різних причин склалося так, що до 70-х років ХХ століття колишній СРСР був єдиною розвиненою країною, в якій початки теорії ймовірностей і вступу до статистики не були включені в шкільні програми. Разом з тим ці теми вивчалися вже в усіх розвинених країнах світу (Великобританія, Німеччина, Франція, США, Польща, Угорщина, Японія та ін.)

Сучасний розвиток суспільства, науково-технічний прогрес,  перехід економіки на ринкові відносини  висунули в 90-х роках ХХ століття нові вимоги до математичної підготовки випускників середньої школи. Саме вимоги суспільства і потреби особистості поставили середню школу перед безумовною необхідністю введення початків теорії ймовірностей і вступу до статистики, що було відображено в освітньому стандарті. Разом з тим, методика  вивчення цих нових для школи тем не була розроблена з врахуванням диференціації навчання і особистісно орієнтованого підходу до навчання. Це значною мірою стосується ліцеїв і класів з поглибленим вивченням математики.

Система вивчення початків теорії ймовірностей і вступу до статистики повинно, безумовно, мати прикладну спрямованість, диференційовану реалізацію і особисто орієнтований підхід. Це означає, що при вивченні теоретичного матеріалу, і особливо при формуванні навичок та умінь, необхідно використовувати змістові прикладні задачі, в тому числі і міжпредметного змісту.

Система задач повинна відбиратись за принципами доступності, прикладної спрямованості, міжпредметних зв’язків, диференціації навчання, послідовного наростання труднощів, експериментально-дослідницького принципу. Задачі не повинні містити попередньо не засвоєних учнями понять і відношень.

3.          Психолого-педагогічні передумови та методичні вимоги до навчання елементів стохастики в 9-х класах з поглибленим вивченням математики

Загальна мета вивчення елементів стохастики у середній школі визначен наприкінці 60-х років ХХ сторіччя академіком Б.В. Гнєденком: „ознайомлення школярів із закономірностями більш широкого типу, ніж класичний детермінізм, а саме – зі статистичними закономірностями”. З того часу завдання розвитку у школярів статистичних закономірностей прийнято називати у методичній літературі задачею формування стохастичного мислення учнів.

Критеріями розв’язання завдання формування стохастичного мислення є: розуміння сутності понять і законів стохастики; вміння розв’язувати якісні стохастичні задачі, тобто вміння робити якісні висновки на базі наявних статистичних даних керуючись провідними міркуваннями, що базуються на інтуїції.

Треба зазначити, що навчання теорії ймовірностей, яке базується лише на вивченні конкретних імовірнісних моделей, може не призвести до розв’язання завдання – формування статистичного мислення учнів. За умови достатнього знайомства з певною імовірнісною моделлю учень зможе формально оперувати з нею достатньо впевнено, проте з точки зору завдань навчання це не є достатнім, оскільки таке оперування ще не свідчить про сформованість стохастичного мислення, оскільки учень може бути безпорадним при побудові нових, навіть досить простих імовірнісних моделей. Достатньо глибоке проникнення у імовірнісні моделі неможливе, якщо не існує фундаменту для цього. Звідси випливає необхідність формування стохастичних уявлень та розвитку імовірнісної інтуїції учнів протягом всього навчання.

Дослідження психологів показують, що людина початково погано пристосована до імовірнісної оцінки, до усвідомлення та ймовірнісної інтерпретації імовірнісно-статистичних даних. Експериментально встановлено, що навіть ґрунтовні знання і розуміння інших розділів математики (які, як правило, мають учні в ліцеях і класах з поглибленим вивченням предмету) ще не забезпечують розвитку стохастичного мислення і не позбавляють навіть від тривіальних імовірнісних забобонів і оман.

Методичною аксіомою можна вважати те, що стохастичне мислення у більшій мірі можна сформувати, але не відразу, не в одну мить. Однак питання про вік, найбільш сприятливий для ефективного розвитку стохастичного мислення, розв’язується не так одностайно .

Досвід показує, що в учня початкової школи недостатньо сформоване уявлення про світ, не вистачає математичного апарату (перш за все звичайних дробів) для формування уявлень про імовірність. Водночас знайомство з простими випадковими експериментами та їх результатами – елементарними подіями, формування поняття випадкової події та її абсолютної ча стоти, основи описової статистики, таблиці, діаграми є можливим і навіть необхідним для введення в початкову школу [5].

Також встановлено, що починати навчання основ теорії ймовірностей у старших класах – малоефективно. Напрацьоване до цього часу прагнення до швидкої формалізації знань, сформоване традиційним курсом математики, бажання засвоїти на уроці перш за все певний набір правил, алгоритмів і методів обчислення фактично замінює формування імовірнісних уявлень формальним вивченням формул комбінаторики і обчисленням ймовірностей за класичною моделлю Лапласа.

Навіть у ліцеях і класах з поглибленим вивченням математики навчання теорії ймовірностей традиційним шляхом дає в основному негативний результат. Навіть для учнів даних класів матеріал здавався складним, формальним, погано засвоювався.

Змальована ситуація схожа на проблеми вивчення геометрії в школі, де на сьогодні, загальновизнаним є необхідність періоду „наочної геометрії” і попередньої роботи з учнями стосовно формуванню просторових уявлень ще до систематичного вивчення курсів планіметрії і стереометрії.

Для того щоб усі теоретико-імовірнісні висновки і конструкції були ясними і зрозумілими учням 9-х класів, необхідно систематизувати стихійно виникаючі інтуїтивні уявлення. Це вимагає, як говорить А.Плоцкі, «умілого введення учня в процес вивчення теорії, розгорнутої пропедевтики теоретичного матеріалу» [4, с.17].

Реальні випадкові події широко представлені в навколишньому світі. Пізнання дитиною навколишнього світу починається від сприйняття одиничних предметів і явищ до утворення конкретних уявлень і від узагальнення останніх до формування понять. Тому, початком формування стохастичних уявлень треба вважати сприйняття дітьми конкретних, випадкових явищ, знайомство з конкретними статистичними сукупностями: „Я пам’ятаю, як одного разу, коли я був ще дитиною, мій батько привів мене на край міста, де на березі стояли верби, і велів мені зірвати навмання сотню листочків верби. Після відбору листя з пошкодженими кінчиками у нас залишилося 89 цілих листочків, коли ми повернулися додому, ми розташували їх у ряд у порядку зростання, як шеренгу солдат. Потім мій батько крізь кінчики листків провів криву і сказав: „Це і є крива Кетле.

Подивись на неї, ти бачиш, що посередності завжди складають більшість і лише дехто піднімається вище або так і залишається внизу” [1, с.84].

Сьогодні ми знаємо цього хлопчика як чудового математика Б.Л. Ван дер Вардена. Його курс математичної статистики наповнений реальними живими прикладами з фізики, хімії, астрономії, геодезії і метеорології, біології і психології, медицини і гігієни, статистики населення, економічної статистики, технічних додатків.

Розрізняють такі три етапи формування стохастичних уявлень школярів:

1)знайомство з найпростішими стохастичними ситуаціями;

2)нагромадження систематизованих уявлень про явища стохастичної природи;

3)створення науково-теоретичної основи стохастичних уявлень.

Перші два етапи пов'язані з формуванням початкових стохастичних уявлень, третій – з вивченням елементів стохастики.

Якщо учень тільки спостерігає за випадковим явищем, а не бере участі у процесі його зародження, то це явище може виявитись для нього чужим, далеким і недостатньо зрозумілим. Треба, щоб учень був поставлений віч-на-віч з самим явищем, а для цього він повинен виконувати певні предметні дії, що призводять до появи випадкових явищ. Виходячи з цього, необхідно включити в процес формування початкових стохастичних уявлень предметні дії учнів з різними об’єктами. Щоб розв’язати цю проблему, звернемося до історії зародження теорії ймовірностей.

Багато задач практики, що служили основою для зародження теорії ймовірностей, як науки, були занадто складними, щоб помітити в них закони випадкового, тоді як в азартних іграх випадок виступає досить чітко і не затушовувалися занадто великим числом факторів, що їх ускладнюють. Крім того, азартні ігри дозволяють спостерігати випадкові явища велике число раз, тобто задовольняють основній вимозі, при дотриманні якої можливий прояв законів випадкових явищ, а саме - їх масовості.

Ця своєрідна роль азартних ігор у виникненні теорії ймовірностей як науки відбилася й у її вивченні. Дотепер, при вивченні початків теорії ймовірностей, у методичних цілях, часто звертаються до прикладів, пов'язаних з підкиданням монети, грального кубика, гральними картами, урнами, рулетками і т.п., за допомогою яких легко проілюструвати поняття випадкової події та її ймовірності і способи підрахунку ймовірностей різних подій.

Однак застосування азартних ігор може мати негативний вплив на моральне виховання учнів. Саме така гра характеризується прагненням будь-що виграти, а при невдачі відігратися. Чи треба дивуватися, що в гравців у всі часи виявлялися тіньові грані характеру. Історія азартних ігор багата спокусами, підробками і злочинами, що знайшло відповідне відображення в літературі і мистецтві. Причиною такого явища служить матеріальний стимул, що закладений в основу правил азартних ігор. Може здаватися, що коли виключити матеріальний зиск й установити інші стимули, то азартні ігри, звільнившись від свого пороку, можуть бути використані в школі. Однак цього неможливо зробити, тому що правила азартних ігор такі, що рано або пізно гра призводить до необхідності встановлення якого-небудь матеріального стимулу, без якого вона стає безглуздою. Тому не може бути і мови про використання азартних ігор у школі.

У практиці навчання елементів стохастики визначені такі організаційні засоби розвитку первісних стохастичних уявлень учнів:

стохастичні ігри;

стохастичні експерименти (експерименти з випадковими витоками);

стохастичні дослідження; уявні стохастичні експерименти; імітація (моделювання).

Завдяки даним організаційним засобам процес навчання школярів стохастики зближується з дослідницьким процесом.

„Всі наші задуми, всі пошуки і побудови перетворюються у тлін, якщо немає в учнів бажання навчатися”, писав В.А. Сухомлинський [6]. Тому вчитель повинен викликати в учнів таке бажання, а це означає, що він повинен сформувати у них відповідну мотивацію. Одним з шляхів досягнення основної мети навчання елементів стохастики є активізація процесу навчання.

Цілі навчання досягаються з використанням різних форм, тобто способів організації навчання. Сучасна дидактика визначає такі форми навчання: урок, семінар, диспут, дидактична гра, практикум, екскурсія, домашні завдання, залік, колоквіум, лабораторні роботи, форуми, роботи в мережі Internet, виконання проектних розробок, дистанційне навчання.

У 9-х класах в процесі вивчення математики застосовуються уроки різних типів, у тому числі і нестандартні: інтегровані, міжпредметні, бінарні, із різновіковим складом учнів. Цікавими елементами цих уроків можуть бути стохастичні ігри, стохастичні експерименти, статистичні дослідження. Це дасть змогу розбудити природні задатки, розвинути здібності дитини, підняти рівень творчості, сприяти розвиткові особистості, виростити інтелектуального учня, плекати талановиту особистість. Наприклад, спрямувати діяльність учнів до «відкриття» поняття ймовірності та математичного сподівання можна, організувати наступний стохастичний експеримент формі гри. Учні класу розподіляються за парами і кожна пара проводить досліди з підкиданням металевої канцелярської кнопки. Якщо кнопка впаде гострим кінцем донизу, то один з гравців записує собі 2 очка, а другий 1 очко. Якщо кнопка впаде гострим кінцем догори, то, навпаки, перший записує 1 очко, а другий 2 очка. Порівнюючи суми очок, вони визначають переможця. Все це проводиться в рамках позакласної діяльності.

На уроці розглядають таблиці частот, які склала кожна з пар гравців. Учням необхідно запропонувати уявити, що число випробувань при проведенні цього експерименту достатньо велике, наприклад 100000. Такий експеримент проводити досить важко, однак ми можемо уявити, які значення частот при цьому найбільш можливо очікувати. Цьому допомагає і огляд таблиці об’єднаних результатів випробувань всіх учнів класу.

Є підстави вважати, що при досить великій кількості випробувань частота появи кнопки гострим кінцем донизу буде наближатись до деякого числа Р (наприклад P ≈ 0.4, якщо відповідні частоти дорівнюють 0.391; 0.412; 0.398; 0.397; 0.401 і т.д.). Вчитель повідомляє, що теоретичне значення частоти яке очікують називають імовірністю випадання кнопки гострим кінцем донизу.

Аналогічне міркування проводиться для випадіння кнопки гострим кінцем угору.

Далі перед учнями ставлять питання про середній виграш. Наприклад, середнє арифметичне виграшів першого і другого гравців відповідно до наведених таблиць дорівнюють:

2*0,95+1*0,45=1,595

1*0,95+2*0,45=1,405

Порівнюючи середнє арифметичне, її обчислене за результатами експерименту для кожної пари, робимо висновок, що практично у всіх парах перші гравці у середньому вигравали більше число очок, ніж другі. Складаються дві послідовності значень середніх арифметичних. Члени кожної з цих послідовностей, за рідким винятком, будуть близькі один до одного. Імовірно, числа першої послідовності будуть наближатися до 1.6, а другої – до 1.4. Прогнозуючи результати експериментів з великим числом випробувань, учні самі висувають гіпотезу про існування деяких теоретично очікуваних чисел М1 і М2, до яких наближаються середні арифметичні відповідних послідовностей при збільшенні числа випробувань. Від учителя вони взнають, що прийнято говорити так: число М1 – це математичне сподівання виграшу першого гравця; число М2 – математичне сподівання виграшу другого гравця.

У класах з поглибленим вивченням математики перевага віддається організації самостійної діяльності учнів у здобутті нових знань, дослідницькому методу вивчення навчального матеріалу.

Результати статистичних досліджень можна тлумачити як створення учнями освітнього продукту, в процесі отримання якого задовольняються потреби у самореалізації і складаються сприятливі умови для розвитку відповідних особистісних якостей: когнітивних, креативних, оргдіяльнісних та ін.

При навчанні елементів стохастики необхідно прищеплювати критичне ставлення до статистичних висновків і узагальнень, вміння правильно тлумачити матеріал, самостійно викривати різного роду фальсифікації, ретельно замасковані під личиною витончено дібраних „правдоподібних” відомостей.

Корисно показати учням конкретні ситуації, в яких тенденційно дібрані статистичні показники можуть служити основою для хибних висновків про події, що відбуваються у політичному і економічному житті суспільства. Розвиток у майбутніх дорослих громадян критичного мислення, вміння розуміти скритий смисл того або іншого повідомлення, протистояти маніпулюванню свідомості індивіда з боку засобів масового інформування.

Розглянемо такий приклад. Господар одного приватного підприємства звілнив більшу частину робітників, а тим що залишилися, знизивь заробітну плату (табл. 1.1). Після чого він заявив, що се редній заробіток працівників на його підприємстві підвищився. Чи так це?

Таблиця 1.1

Зміна заробітної плати

Обчислення середніх характеристик підтверджують, що середні характеристики дійсно збільшилися. До звільнення:

x = 1000 * 200 + 400 * 800 / 1000 =520 грн.

Мода дорівнює 400 грн., медіана дорівнює 400 грн.

Після звільнення:

x = 800 * 200 + 320 * 120/1000 =620 грн.

Мода дорівнює 800 грн., медіана дорівнює 800 грн.

Однак з таблиці видно, що життя робітників не стало кращим, а навпаки, не говорячи про тих, хто втратив роботу.

Оманлива думка про підвищення зарплати складається через звільнення значної частини робітників з низькою зарплатою. Висновки з розв’язання задачі суперечать здоровому глузду.

Наслідком неправильних або суперечливих висновків може бути і неадекватний вибір критеріїв, за якими інтерпретуються статистичні дані. У зв’язку з цим доречно нагадати наступне оповідання.

Кожна з двох фірм, що спеціалізуються з виготовлення взуття відправили до деякої африканської країни свого агента для з’ясування ситуації стосовно реалізації своєї продукції. Агент першої фірми телеграфував: «Чудовий ринок з реалізації взуття – тут 90% населення ходять босоніж». Агент другої фірми сповістив: «Ринок взуття тут відсутній – 90% населення не носять черевиків».

Імовірнісно-статистична лінія забезпечує умови створення учнями індивідуально-творчих продуктів діяльності, що сприяє розвитку креативних якостей людини. Евристичний характер стохастичних умовиводів вимагає так організувати математичну діяльність учнів, щоб вивчення понять і методів доведення тверджень і розв’язування задач відбувалося у формі відкриттів нових специфічних інструментів пізнання оточуючого світу. Особливу роль відіграє тут аналіз імовірнісних парадоксів і несподіванок, що створює сприятливий ґрунт для евристичної діяльності.

Все вище сказане дозволяє виділити такі методичні вимоги до навчання елементів стохастики в 9-х класах в процесі вивчення математики:

1) чітке визначення цілей і завдань навчання нової змістової лінії у зазначених класах;

2) зміст повинен забезпечувати наявність системи теоретичних імовірнісно-статистичних знань, відображати сучасний стан розвитку науки і техніки;

3) забезпечення формування міцних навичок і вмінь при розв’язуванні стохастичних задач;

4) спрямування на встановлення тісного зв’язку імовірнісних моделей з предметним світом, організацію побудови і тлумачення моделей як провідних форм діяльності учнів;

5) навчання повинно бути націленим на використання творчих можливостей школярів як послідовності самостійних „відкриттів”, тобто повинно мати евристичний характер;

6) у навчанні повинні встановлюватися і реалізовуватися міжпредметні зв’язки у якості взаємодії між шкільними дисциплінами, особливо профільними (за профілем ліцею, класу);

7) навчання повинно здійснюва тись на основі профільної і рівневої диференціації;

8) поряд з традиційними засобами навчання мають набути широкого використання засоби інформаційно - комунікаційних технологій.

ВИСНОВКИ ДО ПЕРШОГО РОЗДІЛУ

Пропозиції щодо введення в шкільну програму початків теорії ймовірностей і вступу до статистики висувалися ще в кінці ХІХ століття видатними математиками і відомими діячами системи математичної освіти. Серед математиків ця пропозиція висувалася в Україні, зокрема, М.В.Остроградським  і професором В.П.Єрмаковим.

Система вивчення початків теорії ймовірностей і вступу до статистики повинно, безумовно, мати прикладну спрямованість, диференційовану реалізацію і особисто орієнтований підхід. Це означає, що при вивченні теоретичного матеріалу, і особливо при формуванні навичок та умінь, необхідно використовувати змістові прикладні задачі, в тому числі і міжпредметного змісту.

Система задач повинна відбиратись за принципами доступності, прикладної спрямованості, міжпредметних зв’язків, диференціації навчання, послідовного наростання труднощів, експериментально-дослідницького принципу. Задачі не повинні містити попередньо не засвоєних учнями понять і відношень.

Методичні вимоги до навчання елементів стохастики в 9-х класах в процесі вивчення математики:

1) чітке визначення цілей і завдань навчання нової змістової лінії у зазначених класах;

2) зміст повинен забезпечувати наявність системи теоретичних імовірнісно-статистичних знань, відображати сучасний стан розвитку науки і техніки;

3) забезпечення формування міцних навичок і вмінь при розв’язуванні стохастичних задач;

4) спрямування на встановлення тісного зв’язку імовірнісних моделей з предметним світом, організацію побудови і тлумачення моделей як провідних форм діяльності учнів;

5) навчання повинно бути націленим на використання творчих можливостей школярів як послідовності самостійних „відкриттів”, тобто повинно мати евристичний характер;

6) у навчанні повинні встановлюватися і реалізовуватися міжпредметні зв’язки у якості взаємодії між шкільними дисциплінами, особливо профільними (за профілем ліцею, класу);

7) навчання повинно здійснюва тись на основі профільної і рівневої диференціації;

8) поряд з традиційними засобами навчання мають набути широкого використання засоби інформаційно - комунікаційних технологій.

РОЗДІЛ II МЕТОДИЧНЕ ЗАБЕЗПЕЧЕННЯ ВИВЧЕННЯ ЕЛЕМЕНТІВ СТОХАСТИКИ В 9-Х КЛАСАХ З ПОГЛИБЛЕНИМ ВИВЧЕННЯМ МАТЕМАТИКИ

1.          Організаційно-методичне забезпечення вивчення елементів стохастики учнями 9-х класів на уроках математики

Перейдемо до методики викладання елементів стохастики в 9-х класах з поглибленим вивченням математики.

Операції над подіями, їх геометрична інтерпретація

Оскільки події – це деякі підмножини множини Ω елементарних подій, то для подій можна ввести за аналогією такі самі операції, як і для множин.

На початку уроку з даної теми доцільно провести опитування, щоб пригадати операції над множинами.

Можливі питання:

1.          Яку множину ми називаємо сумою кількох множин?
2.          Як позначається сума множин (двох, кількох)?
3.          Дайте означення добутку множин.
4.          Що ми називаємо різницею двох множин?

Кількість питань за необхідністю можна збільшити.

Основні властивості, якими володіють події Ω, А, В, С як множини:

1. Ǿ .

2. Якщо і , то .

3. А = А.

4. Якщо А = В, то В = А.

5. Якщо А = В, В = С, то А = С.

Нехай і – деякі події.

Сумою подій А і В називають таку подію С, яка відбувається тоді і тільки тоді, коли відбувається принаймні одна з подій А або В.

Діти мають розуміти, що це означає, що кожна елементарна подія, що не належить до множини С, не належить принаймні до однієї з множин А або В, і навпаки, якщо або , то .

Аналогічно визначається сума довільної кількості подій , зокрема, – сума скінченої кількості n подій, а – сума зчисленої кількості подій (тут номер події набуває значень з множини N натуральних чисел). Суму скінченої або зчисленої кількості подій позначають , а також .

Нагадаємо, що для того, щоб одержати об’єднання (суму) двох множин А і В, треба до однієї з низ приєднати ті елементи іншої, яких немає в першій множині.

Позначення, які використовуються для сум:

.

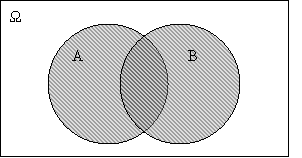
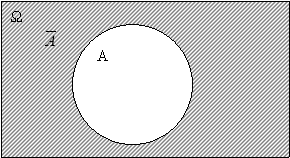
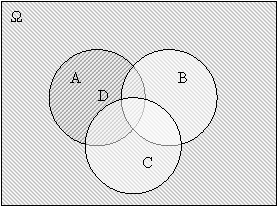
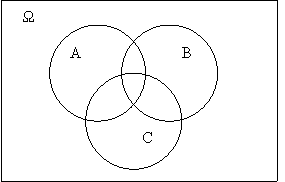
Геометричне тлумачення суми подій А і В подано на рисунку 19, де прямокутником зображено множину елементарних подій Ω, один з кругів – подія А, іншими – подія В застрахована множина – подія

Рис.2.1. .

Пояснення нового матеріалу супроводжується прикладами.

Приклад 1. Нехай – множина елементарних подій, що відповідає підкиданню експериментального кубика один раз, – подія, що полягає у випаданні на верхній грані числа, кратного 3, – подія, що полягає у випаданні парного числа. Тоді , – подія, яка полягає в тому, що на верхній грані кубика випаде або число, кратне 3 (відбудеться подія А), або число, кратне 2 (відбудеться подія В). – подія, яка полягає в тому, що на верхній грані кубика випаде парне число (відбувається подія В), кратне 3 (відбувається подія А). (рис. 20).

Ω

А В

Рис. 2.2.

Добутком подій А і В називають таку подію С, яка відбувається тоді і тільки тоді, коли відбуваються обидві події А і В.

Це означає, що кожна елементарна подія Е, що належить С, належить також до обох множин А і В, тобто і і навпаки, якщо і то . Отже, .

Добуток подій А і В позначають також А ∙ В, або просто АВ. Аналогічно визначається добуток довільної кількості подій , зокрема – добуток скінченої кількості n подій, – добуток зчисленної кількості подій. Добуток скінченої або зчисленної кількості подій позначають , а також .

Нагадаємо, що для того, щоб одержати переріз (добуток) двох множин А і В треба взяти все елементи, які належать до обох цих множин.

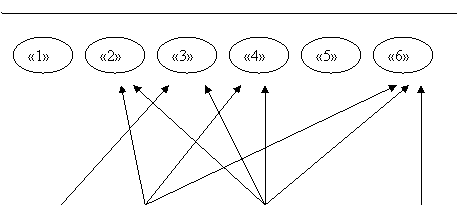
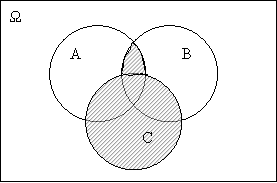
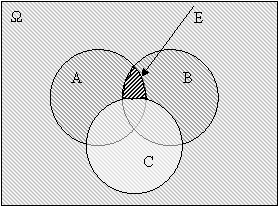
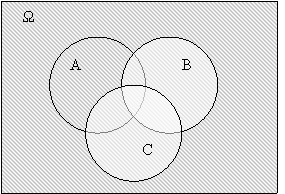
Геометричне тлумачення добутку подій А і В Подано на рисунку 21, де заштрихована множина точок – подія .

Рис. 2.3. .

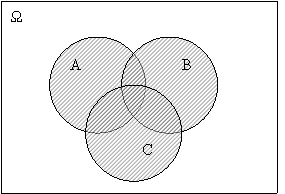
Різницею подій А і В (А мінус В) називають таку подію С, яка відбувається тоді і тільки тоді, коли відбувається подія В.

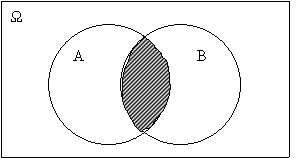
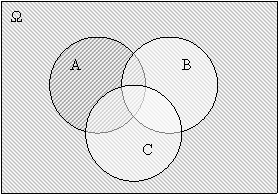
Це означає, що кожна елементарна подія Е, що належить до множини С, належить також до множини А і не належить до множини В, і навпаки, якщо і , то . Адже С = А\В. Тоді різницю подій А і В (А мінус В) позначають як А – В.

Нагадаємо, що для того щоб одержати різницю множин А і В, треба із множини А вилучити всі елементи множини В. Геометричне тлумачення різниці подій А і В подано на рисунку 2.2, де заштрихована множина точок А\В.

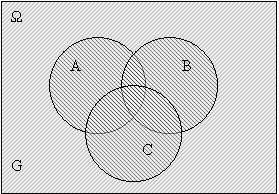
Важливим є означення протилежної події. Різницю Ω/А називають подією, протилежною до події А і позначають . Отже, подія протилежна до А, відбувається тоді і тільки тоді, коли не відбувається подія А. Очевидно, події А і несумісні. Геометричне тлумачення протилежної події подано на рисунку 2.3, де заштрихована множина точок – подія , протилежна до події А.

Рис. 2.3. А\В. Рис. 23. .

Прикладом для пояснення протилежної події може стати такий:

Приклад 2. В урні знаходяться білі й чорні кулі, які виймають по одній. Множина елементарних подій Ω = {«біла куля», «чорна куля»}. Якщо подія А полягає в тому, що вийняли білу кулю, то протилежною буде подія, коли вийняли чорну кулю.

Подія , протилежна вірогідній, є неможливою. Неможливій події відповідає порожня множина можливих наслідків випробування.

Важливим для учнів є знання основних законів.

Нехай А, В і С – довільні випадкові події, Ǿ – неможлива подія. Введені операції над подіями задовольняють таким законам:

1. – закон подвійного заперечення;

2.

3. АВ = ВА  комутативні (переставні) закони додавання і множення

4.

5.     асоціативні закони додавання і множення

6. – перший дистрибутивний (розподільний) закон

7. – другий дистрибутивний (розподільний) закон

8. А + А = А

9. А ∙ А = А

10.

11. Ǿ

12. A + Ω = Ω

13. AΩ =A

14. A + Ǿ = A

15. А Ǿ = Ǿ

16.

17.   закони двоїстості (правила де Моргана)

Рівності 1 – 5, 8 – 15 випливають безпосередньо з наведених вище означень.

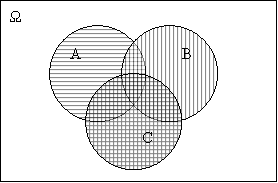
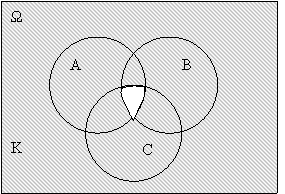
Розглянемо, наприклад, рівність 7: .

Геометрично цей закон можна проілюструвати так, як показано на рисунку 2.4 та рисунку 2.5. При порівнянні цих зображень, можна впевнитися, що множини збігаються.

                  Рис. 2.4. .                                Рис. 25. .

Система вправ до цієї теми:

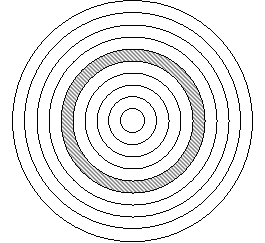
1. Мішень складається з 10 кругів, обмежених концентричними колами з радіусами : . Подія полягає у влученні в круг з радіусом . Що означають події:

1) ;

2) ;

3) ;

4) ;

5) . [17, стор. 12].

1) Влучено принаймні в один круг з шести, обмежених колами, радіуси яких дорівнюють , , , , , (рис. 26).

2) Влучено в круг, обмежений колом з радіусом .

3) Влучено в кільце, обмежене колами з радіусами та , k=1, 2….

                         Рис. 2.6.                                           Рис. 27.

4) Ця подія неможлива, бо вона означає, що влучено в круг з радіусом і при цьому не влучено в круг з радіусом , а за умовою < .

5) Не влучено в круг з радіусом , k= 1, 2…10.

2. Маємо події А, В и С. Записати вирази для подій, які полягають в тому, що:

а). настала лише подія А;

б). настали А і В, С не настала;

в). настала принаймні одна з цих подій;

г). не настала жодна з подій;

д). настали всі три події;

е). настало не більше двох подій.

Зобразити ці події за допомогою кругів Ейлера.

а). (рис. 28.) б). (рис. 2.9.)

Рис. 2.8. D.   Рис. 2.9. E.

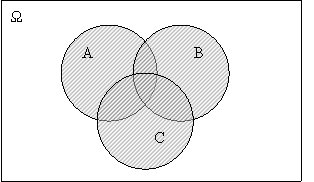
в)., г). (рис. 31.)

де АВ = А·В. (рис. 30.)

Рис. 2.10. F.  Рис. 2.111. G.

д). (рис. 2.12.) е). (рис. 2.13.)

Рис. 2.12. H.  Рис. 2.13 K.

3. В полі зору мікроскопа знаходяться чотири клітини. За час спостерігання кожна з них може як розділитися, так і не розділитися. Розглядаються події:

A – «розділилась лише одна клітина»;

B – «Розділилась хоча б одна клітина»;

C – «Розділилося не менше двох клітин»;

D – «Розділилося рівно дві клітини»;

M – «Розділилося рівно три клітини»;

F – «Розділилися усі чотири клітини».

Запишіть словами вирази 1 – 7.

Чи вірні рівності 8, 9?

1) , 2) , 3) , 4) , 5) , 6) , 7) ,

8) , 9) . [6, стор. 256].

1) – «розділилися усі чотири клітини»;

2) – «розділилась хоча б одна клітина»;

3) – «розділилась лише одна клітина»;

4) – «розділилась хоча б одна клітина»;

5) – «розділилося не менше двох клітин»;

6) – «розділилося не менше двох клітин»;

7) – «розділилися усі чотири клітини»;

8)

, , отже рівність вірна;

9)

Рівність не вірна, бо .

4. Назвіть для вказаних подій протилежні:

A – «Випало два герба» (підкидання двох монет);

B – «Вийняли білий шар» (виймають один шар з ящика, де лежать білі, червоні та сині шари);

C – «Три влучання» (зробили три постріли по мішені);

M – «Не більше двох влучань» (п’ять пострілів);

D – «Хоча б одне влучання» (п’ять пострілів);

F – «Виграв Петренко» (партія в шахи Петренко – Василенко).

– «випало дві цифри, або цифра та герб»;

– «вийняли червоний, або синій шар»;

– «менше, ніж три влучання»;

– «не менше трьох влучань»;

– «жодного влучання»;

– «виграв Василенко, або нічия».

5. Які з наступних пар подій не сумісні:

а) навмання вибране натуральне число від 1 до 100 включно ділиться на три; є простим числом;

б) влучання при одному пострілі; промах;

в) виграш у футбольному матчі; програш.

б) влучання при одному пострілі; промах; та в) виграш у футбольному матчі; програш.

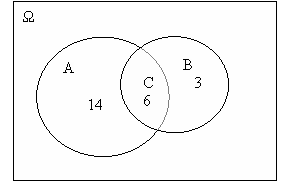
6. З 25 учнів 20 чоловік займаються спортом (подія А), 9 – музикою (подія В), 6 – музикою і спортом (подія С). З’ясувати, в чому складаються події , та . [33, стор. 15].

, С = 6.

– «14 учнів займаються лише спортом»;

– «троє учнів займаються лише музикою».

Отже, і музикою і спортом займаються 23 учня, а тому подія полягає в тому, що лише 2 учні з 25 не займаються ні музикою, ні спортом (рис. 2.14).

Рис. 2.14.

7. Брауну, Джонсу, та Сміту висунуто звинувачення в співучасті в пограбуванні банку. Грабіжники втекли на автомобілі, що очікував їх за рогом. На допиті Браун розповів, що злочинці були на блакитному «Б’юіку», Джонс дав свідчення, що це був чорний «Крайслер», а Сміт стверджував, що автомобіль був марки «Форд Мустанг» ні в якому разі не блакитний. Стало відомо, що прагнучи заплутати слідство, кожен з них вказав вірно лише або марку машини, або її колір. Якої марки та якого кольору був автомобіль, на якому втекли грабіжники банку? [33, с. 326].

Позначимо події так: в пограбуванні брав участь автомобіль

A – блакитного кольору;

B – марки «Б’юік»;

C – чорного кольору;

D – марки «Крайслер»;

E – марки «Форд Мустанг».

В кожному окремому свідченні освітлюється пара подій, одна з яких відбулася, тобто відбулася сума цих двох подій.

– свідчення Брауна;

– свідчення Джонса;

– свідчення Сміта.

З того, що ці всі події відбулися випливає, що відбувся їх добуток

Якщо вилучити неможливі події, тобто ті події, що не можуть відбутися (наприклад: - злочинців чекав автомобілі, одночасно і блакитного, і чорного кольору марки «Форд Мустанг»), залишається лише подія . Можна зробити висновок, що грабіжники втекли на чорному «Б’юіку».

8. Чи може сума двох подій А та В співпадати з їх добутком?.

Так, може, якщо події рівнозначні, тобто якщо з події А випливає подія В і, навпаки з події В випливає подія А.

Для більш реального представлення подій, які описані в задачі №1 використовується зображення мішені, яка складається з концентричних кругів, або гра «Дарц».

Задача №2 відкриває вчителю великий простір для творчості. Подану суху, майже шаблонну задачу можна наповнити змістом – реальними подіями, які можуть як перетинатись, так і не перетинатись.

Наприклад: В інкубаторі закладено три яйця, які позначено цифрами 1, 2, 3. В заздалегідь відомий час з них мають вилупитись: з першого – курча, з другого – гусеня, з третього – каченя. Подія А полягає в тому, що вилупилось курча, В-гусеня, С – каченя.

Необхідно привчити учнів до використання як знаків « *», «·» так і « », як знака « +», так і « ». В одному завданні (в одному виразі) використовувати лише один з пари знаків.

Важливим для учнів є вміння зображати вирази операцій над подіями графічно, за допомогою кругів Ейлера.

Ось приблизний алгоритм розв’язку завдання на зображення подій за допомогою кругів Ейлера:

1. Якщо необхідно, спрощуємо чи перетворюємо поданий вираз.
2. Прямокутником зображаємо множину елементарних подій Ω.
3. На ній розміщуємо у вигляді кругів випадкові події, позначаємо їх літерами (необхідно врахувати можливі умови, наприклад А = В, чи АВ = Ǿ, ).

Якщо розглядаються три випадкові події, найбільш прийнятне таке розміщення, як показано на рисунку 2.15.

Рис. 2.15.

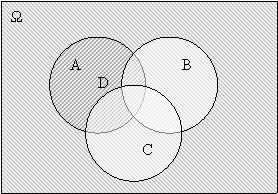
4. Послідовно, враховуючи дужки штрихуванням показуємо події які є результатом кожної операції.

5. Виділяємо шукану подію (її можна заштрихувати унікальним способом, або іншим кольором, позначити границі) та позначаємо її літерою.

Якщо ж шукана подія сформульована словами, необхідно самостійно скласти вираз.

Розв’яжемо за цим алгоритмом завдання №2, а).

Нехай шукана подія – D.

1. .

2. рисунок 2.16. 3. рисунок 2.17.

Рис. 2.16.                           Рис. 2.17.

4.1. (рис. 2.18) 4.2. (рис. 2.19)

Рис. 2.18.       Рис. 2.19.

5. рисунок 2.20.

Рис. 2.20.

При розв’язуванні завдання №8 доречно розглянути такий приклад:

Нехай здійснюється один постріл по мішені. Приймемо таку умову, що влучання в мішень неодмінно призводить до її руйнування і ніяким іншим засобом мішень зруйнувати не можливо. Тоді дві події: А – влучання в мішень і В-руйнування мішені еквівалентні (А = В).

Для них

А + В = А = В

А*В = А = В.

2.          Використання комп’ютерних програм на уроках математики при вивченні елементів стохастики в 9-х класах

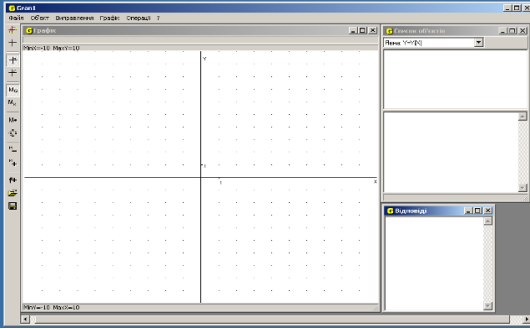
Під час опрацювання статистичних даних, особливо коли вони мають досить великий обсяг, доводиться мати справу з великою кількістю нетворчих, нецікавих, рутинних обчислювальних і графічних операцій. Особливо це стає проблемою, коли вчитель не має достатньої кількості учбових годин, а є бажання запропонувати учням цікаві завдання, або й залучити їх самих до збирання та обробки статистичних даних. Тут в нагоді стане меж предметний зв’язок математики та інформатики.

Заняття з математики, орієнтовані на використання педагогічних програмних засобів навчання, мають проходити у відповідно оснащеному досконалими технічними засобами класі. У таких класах мають вивчатися всі навчальні предмети без винятку, а не лише основи інформатики та обчислювальної техніки. Це сприятиме розширенню і поглибленню інтеграції навчальних предметів, та дасть можливість оволодіти елементами нових інформаційних технологій, з використанням їх на практиці.

Прикро, але сьогодні в школі не використовується в повному обсязі можливості прикладного програмного забезпечення для різноманітних навчальних дисциплін. Роботу з комп’ютером залишають викладачеві інформатики. Нажаль, вчителі інших предметів досить рідко використовують можливість зацікавити своїх учнів дисципліною, що викладають, урізноманітнити свої уроки та полегшити як свою, так і учнівську роботу.

Міністерством освіти і науки України під час вивчення в школі курсу алгебри та початків аналізу, а також деяких розділів геометрії, для аналізу функціональних залежностей та статистичних закономірностей рекомендовано використання педагогічних програмних засобів GRAN1 та Derive. Вони призначені насамперед для розв’язування широкого класу задач шляхом моделювання об’єктів, що фігурують в умові задачі.

Розглянемо можливості застосування програмного засобу GRAN1 при викладанні початків теорії ймовірностей. За його допомогою можна виконати велику кількість обчислень і графічних побудов. Він полегшує опрацювання статистичного матеріалу, оскільки всі обчислення, побудови графіків (полігонів частот, гістограм, функцій дискретних та неперервних розподілів відносних частот), визначення деяких параметрів розподілу (середнє значення, характеристики розсіювання і т. п.) комп’ютер виконує автоматично і практично миттєво – досить звернутися до відповідної послуги програми. Тому з’являється можливість основну увагу зосередити на з’ясуванні сутності явищ, які вивчаються, їх властивостей, причинно-наслідкових зв’язків, різних особливостей окремих їх проявів. Усі рутинні операції, пов’язані з виконанням обчислень та графічних побудов, перекладаються на комп’ютер.

GRAN1 досить легкий в застосуванні, з простим інтерфейсом. Він не вимагає ні від вчителя, ні від учнів якихось особливих знань з інформатики чи програмування. Достатньо буде мінімума навичок користувача. Є змога обрати українську мову або російську мову.

Робоче вікно GRAN1 (Windows) містить панель інструментів, меню та три вікна: Графік, Список обєктів та Відповіді (рисунок 2.21). Надалі GRAN1 (W) будемо позначати як GRAN1.

Рис. 2.21

У вікні Графік будуються графічні зображення об'єктів. При переміщуванні мишки у вікні відповідним чином переміщується і покажчик координат (зображується перехрестям) та виводяться значення координат у верхній частині вікна. Цей покажчик можна переміщувати і за допомогою клавіш управління курсором. У вікні також можна робити пояснювальні написи за допомогою міток. За допомогою послуги меню Графік / Параметри вікна «Графік» можна встановити різні характеристики цього вікна.

Вікно Список обєктів містить список для вибору типу об'єкту, що буде створюватися, список введених об'єктів та панель виведення інформації про поточний об'єкт (об'єкт на якому знаходиться курсор – зображуються інверсним кольором у списку об'єктів). Операції програми виконуються над поточним об'єктом або над відміченими об'єктами.

У вікні Відповіді подаються результати виконання операцій програми.

Меню програми складається з наступних пунктів: Файл, Об’єкт, Виправлення, Графік, Операції та Допомога(«?»). Послуги пункту меню Файл призначені для запису або читання математичних об'єктів у файл чи з файлу на диску. Пункт Об’єкт обслуговує роботу з математичними об’єктами. Послуги Виправлення призначені для роботи з буфером обміну. Графік – для проведення операцій над графіками, що відповідають введеним математичним об'єктам. Послуги пункту меню Операції призначені для виконання певних математичних операцій над введеними об'єктами.

Окремі послуги меню винесено на панель інструментів та, залежно від призначення, деякі пункти повторено в контекстних меню вікон програми.

Для ефективного використання педагогічного програмного засобу GRAN1 необхідно побудувати послідовність уроків таким чином, щоб на одному з уроків можна було б з учнями розібрати негроміздку задачу, побудувати вручну полігон чи гістограму. А на наступному уроці в кабінеті, обладнаному комп’ютерами, цю ж саму задачу розв’язати за допомогою GRAN1. Це буде своєрідним повторенням, та самоперевіркою. Діти зможуть одразу відчути переваги використання GRAN1, як програмний засіб полегшує обробробку статистичних даних та скорочує час, затрачаний на розв’язання задачі. Потім можна запропонувати учням самостійно розв’язати задачі з більшим об’ємом статистичних даних.

Звичайно, якщо діти ще не працювали з цією програмою, то для роботи в комп’ютерному кабінеті краще запланувати зпарений урок, в першій частині якого провести знайомство з GRAN1 (не обов’язково при цьому розглядати створення математичного об’єкту «статистична вибірка», можна почати з простої явно заданої функції). Другий з двох спарених уроків присвячуємо саме розв’язанню задач за допомогою GRAN1. Один з варіантів проведення цих уроків – лабораторні роботи.

Осі орієнтовний зміст лабораторних робіт наведено нижче в косих дужках (\\) – коментарі для викладача:

Лабораторна робота №1.

Обробка статистичних даних за допомогою GRAN1.

Мета: узагальнити та систематизувати знання, сформувати необхідні вміння та навички розв’язування статистичних задач за допомогою GRAN1.

Обладнання: ПК, програмний засіб GRAN1.

Порядок роботи:

Задача 1: Проведіть експеримент: підкиньте 50 разів дві гральні кості і запишіть суму для кожного кидка. Яка сума з’явилась частіше? Яка – найменшу кількість разів? Яке число з’явилось частіше: 3 або 12?

Ми вже розглядали розв’язування цієї задачі.

Таблиця 2.1 – таблиця експерименту:

Таблиця 2.1

Крок 1. Актуалізація знань.

Цей крок не обов’язково включати до методичних рекомендації, які роздаються учням. Опитування необхідно провести ще до початку роботи за комп’ютером.

Дайте відповіді на питання:

1. Що ми називаємо елементарною подією? Наведіть приклади.
2. Дайте означення випадкової події. Приклад випадкової події.
3. Поясніть різницю між елементарною подією і випадковою подією, використовуючи конкретний приклад.Дайте означення статистичної ймовірності елементарної події.
4. Дайте означення статистичної ймовірності випадкової події.
5. За якими формулами обчислюються статистичні ймовірності подій?
6. Який алгоритм побудови полігону для дискретного варіаційного ряду частот?

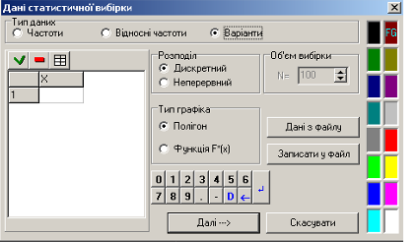
Крок 2. Початок роботи.

Завантажте GRAN1.

Крок 3. Створення об’єкту «статистична вибірка».

В вікні Список обєктів зі списку для вибору типу об’єкту обираємо статистичну вибірку. Використавши або контекстне меню цього вікна (права кнопка миші), або головне меню Об’єкт, обираємо послугу Створити. На екрані з’являється вікно Дані статистичної вибірки (рисунок 2.23).

Рис. 2.23

Перемикач в розділі Тип даних ставимо навпроти пункту Варіанти.

В таблицю вводимо наші дані. Після вводу числа, натискаємо Enter і з’являється новий рядок для наступного числа. В нагоді стануть кнопки Вставити рядок(), Вилучити рядок() та Очистити таблицю().

В розділі Тип графіка обираємо Полігон.

За бажанням можемо змінити колір, яким буде зображено наш полігон, вибравши його в палітрі.

Тиснемо на кнопку Далі. В нижній частині вікна Список обєктів зявляться підраховані деякі параметри нашої виборки.

Крок 4. Побудова полігону варіаційного ряду.

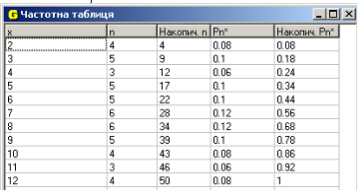
Скориставшись об’єктом панелі інструментів , або пунктом меню Графік / Побудувати, будуємо полігон варіаційного ряду.

Для наочності можна зменшити масштаб, або в послузі меню Графік / Масштаб / Масштаб користувача обрати оптимальний. Масштаб відображається у верхній частині вікна. Ті значення на осях, які нас цікавлять, можна позначити, використовуючи мітки.

Крок 5. Вивчення частотної таблиці.

За допомогою послуги меню Операції/Статистика / Частотна таблиця відкриваємо таке вікно, як показано на рисунку 44.

Рис. 2.24.

Розгляньте цю таблицю, які дані містяться в кожній колонці? Які можна зробити висновки за інформацією, отриманою з частотної таблиці?

Крок 6. Відповіді.

Тепер ми можемо відповісти на поставленні питання. Найчастіше з’явилися суми 7 та 8; найменшу кількість разів – 4 та 11. Частіше отримували суму 3, ніж 12. (див Приклад1.gr1)

Використовувати GRAN1, оброброблюючи статистичні дані, дуже зручно, але існують деякі мінуси. Розрахунки виконуються автоматично, учень навіть не замислюється, що саме: математичне сподівання, моду чи середнє квадратичне, йому необхідно обчислити, щоб відповісти на запитання, поставлене в задачі. GRAN1 не вимагає у каристувача знання формули за якою необхідно вести розрахунки.

GRAN1 доцільно використовувати як засіб наглядності. Вчитель може заздалегідь до уроку створити математичний об’єкт «статистична вибірка» з необхідними даними і параметрами та зберегти його. А на уроці лише відкрити програму та показати учням готові результати, не витрачаючи час на побудови того ж полігону на дошці, підрахування різних властивостей вибірки за формулами.

Нажаль, не завжди є змога провести урок математики в кабінеті, обладнаному комп’ютерами чи використати один комп’ютер для демонстрації наочності і прикладів. В такому випадку можна використати GRAN1 для розробки дидактичного матеріалу. Наприклад, створити картки для розглянутого нами приклада, як наочне представлення простої статистичної вибірки, або більш складної задачі з великим об’ємом статистичних даних.

Ось приклади задач, розв’язаних за допомогою GRAN1:

Задача 2: Побудувати дискретний варіаційний ряд і накреслити полігон для розподілу 45 пар чоловічого взуття, проданого магазином за день:

41, 40, 39, 40, 42, 41, 42, 40, 44, 41, 43, 42, 43, 42, 39, 41, 39, 41, 42, 43, 37, 41, 42, 43, 38, 41, 40, 42, 41, 40, 40, 42, 40, 41, 39, 40, 44, 38, 41, 40, 39, 38, 43, 42, 41 [14, стор. 504].

Першим етапом є самостійне розв’язання задачі. Вона не дуже складна, тому вчитель може обрати один з двох варіантів: або розв’язувати її на уроці, або дати як домашнє завдання перед уроком в комп’ютерному кабінеті.

Проаналізувавши статистичні дані, отримаємо таблицю 2.2.

Таблиця 2.2

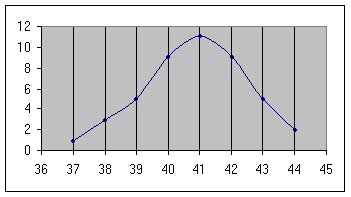
Відкладаємо на осі ОХ розміри взуття, а на осі ОY – кількість проданих магазином пар. Масштаб обираємо таким чином, щоб висота полігону відносилась до його ширини, як 3:5 (рисунок 2.25).

Рис. 2.25

Наступним етапом розв’язання цієї задачі є перевірка отриманих результатів за допомогою GRAN1.

Діти створюють математичний об’єкт «статистична вибірка», заносять статистичні дані в таблицю, потім отримують полігон, параметри вибірки та, за допомогою послуги меню «Операції/Статистика / Частотна таблиця», частотну таблицю.

Порівнявши полігон, отриманий самостійно, та той, що одержано за допомогою GRAN1, діти зможуть адекватно оцінити свою роботу, та побачити власні помилки. Вчитель повинен стати координатором ціого процесу.

Наступною має стати задача з більшим об’ємом статистичних даних, або ж з даними, що представлені дробами чи великими числами.

Задача 3: Підприємство «Аква» випускає різноманітну продукцію, щодня товар реалізується, причому різним покупцям. Керівник зацікавився, які з партнерів цього підприємства є найбільш активними покупцями, а які ні. Розгляньте реєстр видаткових накладних фірми «Аква», де вказано суми та назви фірм, дайте відповідь на це питання.

Для більш зручної обробки даних, в зазначеній таблиці поряд з колонкою, що містить назву покупця, розміщено колонку з номером, який присвоєно кожному покупцю

Для зручності введення даних, кожному учневі роздається таблиця реєстру.

Родзинка задачі полягає в тому, що питання поставлено не в формалізованій формі. Звісно, тут нама б було чаго робити, якщо б задача вимагала знайти середнє значення, або просто побудувати полігон.

Створивши за введеними данними математичний обєкт (див. Приклад3.gr1), ми одразу отримаємо відповідь на питання: кого можна назвати постійним клієнтом фірми «Аква». Побудова полігону – це лише наочне представлення. За частотною таблицею (див. додаток 8) можна охарактеризувати кожного з покупців.

Отже, постійним клієнтом фірми «Аква» є покупець, позначений номером 8, – це фірма «Інвест». І маємо цілу низку клієнтів (16 фірм), якім «Аква» за розглянутий період постачала свій товар лише один раз:

4 – Приморец;

14 – Промтепловоз ДЗРТ;

15 – ТЕХРЕМ ООО;

17 – Лик-СВ ООО;

20 – Прогресс;

21 – Транзас Украина;

24 – Донэлектро ООО;

26 – Азовкомплект ООО НПП;

27 – Модус-Сервис ООО ПКФ;

28 – Промсбыт ООО;

30 – Астапов;

32 – Керченський судоремонтный завод;

33 – НКМЗ ЗАО;

34 – Технохим ЗАО;

36 – Порт Мариупольский торговый;

38 – Индустриал-2000.

Процес розв’язання задач за допомогою GRAN1 дозволить перевірити учнів на наявність знань про способи оцінки даних за розподілом частот, виявлення міри центральної тенденції (центрального положення).

Найпростіше знайти міру центральної тенденції за допомогою моди.

Мода – це значення ознаки, яке зустрічається найчастіше в данному ряді розподілу.

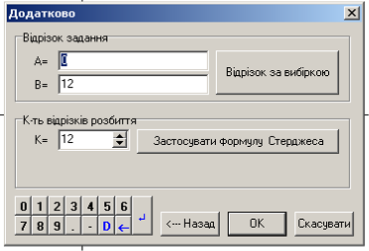
Проте не кожна сукупність значень має єдину моду в строгому розумінні ціого означення. Якщо два сусідніх значення мають однакову частоту і вона більше від частоти будь-якого іншого значення, мода є середнє цих двох значень. Повернемося до першої задачі. Найчастіше в нас з’явилися суми 7 та 8, а .

GRAN1 також дозволяє будувати гістограми, для цього в вікні «Дані статистичної вибірки», перемикач в розділі «Розподіл» ставимо навпроти пункту «Неперервний», в розділі «Тип графіку» замість полігону з’являється вибір гістограми. Після введення даних і натиснення кнопки «Далі» переходимо до вікна «Додатково» (рисунок 2.26), де обираємо відрізок, на якому будуємо гістограму, та кількість відрізків розбиття.

Рис. 2.26

Якщо витрати часу на занесення даних досить значні, можна скористуватися послугами Записати у файл та Дані з файлу. Це доречно, якщо комп’ютери об’єднано в локальну мережу. Вчитель при підготовці до уроку створює об’єкт статистична вибірка та заносить данні, потім, натиснувши на кнопку Записати у файл в вікні Дані статистичної вибірки, зберігає статистичні дані в файлі (обирати назву файлу доцільно якомога близькою до змісту). Потім учні при роботі з GRAN1, замість того, щоб вручну вводити дані, натискають кнопку Дані з файлу і таблиця статистичних даних автоматично заповнюється.

Задачі, рекомендовані до розв’язання за допомогою GRAN1:

Задача 4.

4.1. Побудувати полігон відносних частот появи спостережених значень досліджуваної величини, якщо задано розподіл частот (таблиця 10)

Таблиця 2.3

4.2. За данними вправи 4.1. побудувати гістограму інтервального розподілу відносних частот появи спостережених значень досліджуваної величини, якщо розглядаються інтервали (-3,5; -2,5), (-2,5; -1,5), (-1,5; -0,5), (-0,5; 0,5), (0,5; 1,5), (1,5; 2,5), [2,5; 3,5].

4.3. Знайти середнє арифметичне спостережених значень досліджуваної величини та середнє квадратичне. [14, стор. 144].

Задача 5. Побудувати ряд розподілу і полігон частот для вибірки, яку утворюють відхилення результатів вимірювання відстані між двома точками від істиного значення цієї відстані: -50, 20, -10, 10, 20, -50, -20, -10, 40, -20, -30, -10, 10, 20, -40, 50, -10, 10, 50. [14, стор. 161].

Задача 6. При визначенні похибки вимірювального прикладу зроблено 40 вимірів, при яких зафіусовано похибки: -2,5; 3; 4; 2; 0,5; -1; 2; 4; -4; 0; -05; -0,5; 1; 0,5; 2,5; -0,5; 2; 1; -4; -2; -1; 1,5; 0,5; 4; -1,5; -1; 0; 1; 0; 1; -0,5; 1,5; 0,5; 0,5; -0,5; -1,5; -0,5; -1; 2; 0,5.

Побудувати інтервальний ряд розподілу частот і гістограму частот, поклавши n=8. [14, стор. 161].

Задача 7. 9-А клас, що складається з двадцяти учнів, здавав норматив зі стрибків у висоту. Було зафіксовано такі результати: 137, 140, 143, 135, 142, 139, 141, 137, 142, 131, 145, 138, 141, 143, 130, 138, 140, 135, 137, 138. норматив зараховується, якщо отримано результат від 140 і вище. Скільки учнів будуть перездавати стрибки у висоту? Який з результатів найкращій?

Задача 8. На 100 однакових за розмірами навмання вибраних ділянках землі в даному районі висаджено по 100 саджанців фруктових дерев. Для кількості саджанців, що прийнялися, побудовано інтервальний розподіл спостережених частот (таблиця 2.3)

Таблиця 2.3

Визначити значення функції розподілу частот в кінцях заданих інтервалів і побудувати її графік. [14, стор. 161].

Задача 9. На 100 однакових за розмірами навмання вибраних ділянках землі з однаковою кількістю внесених добрив зібрано різний урожай зерна. Результати проведених спостережень подано у таблиці 2.4

Таблиця 2.4

Побудувати полігон частот. Визначити середнє арифметичне і середнє квадратичне відхилення. [14, стор. 161].

Задача 10. Кількість викликів, що поступають на АТС за 1 годину, є випадкова величина. Для спостережень протягом кількох днів навмання вибрано 10 разів по 1 годині між дев’ятою і дванадцятою годиною і одержано такі результати: таблиця 2.5.

Таблиця 2.5

Побудувати полігон частот. Знайти середнє арифметичне і середнє квадратичне відхилення для досліджуваної величини. [14, стор. 161].

Задача 11. Одна і та ж віддаль вимірюється багато разів. Результати 10 різних вимірювань наведено в таблиці 2.6

Таблиця 2.6.

Побудувати полігон частот. Знайти числові характеристики статистичної вибірки. [14, стор. 162].

Задача 12. Візьміть сторінку будь-якого тексту, який не містить цифри та будь-які спеціальні знаки, а лише слова, що складаються з літер. Які літери найвживані, а які навпаки мало використовуються в словотворенні. Для розгляду не враховувати знаки пунктуації.

2.3. Експериментальне дослідження ефективності вивчення елементів

стохастики в 9-х класах з поглибленим вивченням математики

та аналіз його результатів

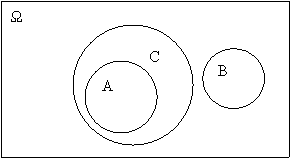
Для підтвердження гіпотези дослідженя, було вирішено провести формуючий експеримент. Для цього був обраний 9-ий клас з поглибленим вивченням математики та фізики загальноосвітньої школи села Чкалове Веселівського району. Клас, обраний для апробації експериментального дослідження складається з 28 учнів, рівень успішності достатньо високий. Відчувається стійкий усвідомлений інтерес дітей до математики.

Під час проведення занять з розділу «Початки теорії ймовірностей та математичної статистики» в 9-му класі була застосована експериментальна методика викладання теоретичного матеріалу, введення основних понять, формування необхідних знань та вироблення вмінь, навичок розв’язання імовірнісних задач. Розроблена система практичних завдань використовувалась на уроках при поясненні нового матеріалу, для повторення, перевірки, систематизації та закріплення вже отриманих знань та умінь, для домашніх завдань. Окремі задачі в трохи зміненому за змістом вигляді були включені в навчальний процес як евристичні (як проблемні ситуації). Використання проблемного методу навчання дуже ефективне в класах з поглибленим вивченням математики.

Задачі викликали інтерес та зацікавленість у учнів, вони охоче та успішно їх розв’язували. Особливо привабливими виявились задачі експериментального характеру, які потребували проведення конкретної кількості випробувань. Фіксація результатів та їх обробка проводилась дуже ретельно. Для дітей було важливим виконати завдання не для того, щоб отримати високий бал, а з цікавості самостійно отримати статистичні результати та зробити необхідні висновки.

При вивченні тем «Поняття випадкової події. Вірогідна та неможлива події», «Операції над подіями» виникли деякі ускладнення з розумінням учнями геометричних зображень відношень між подіями. Вирішено було запропонувати задачі подібного змісту:

Встановити за рисунком 2.2. які відношення між множинами А, В та С. Чи спричиняє множина В множину С? Чи є спільні елементарні події у множин А та В, у множин А та С?

Рис. 2.28

Було проведено три уроки в кабінеті, обладнаному комп’ютерами. два з яких – у вигляді лабораторних робіт: «Знайомство з програмою GRAN1» та «Обробка статистичних даних за допомогою GRAN1». Робота з комп’ютером викликала в учнів позитивні емоції. Вони були вражені і здивовані, що інформаційні технології можуть стати корисними не лише на уроках інформатики. Діти відчули, як педагогічний програмний засіб полегшує їхню роботу, та виникли питання: які ще задачі з математики можна розв’язати за допомогою GRAN1, чи існують інші програми для розв’язування математичних задач.

Задача до теми «Простір елементарних подій» (Проведіть наступний експеримент: підкиньте 50 разів дві гральні кості і запишіть суму для кожного кидка. Яка сума з’явилась частіше? Яка – найменшу кількість разів? Яке число з’явилось частіше: 3 або 12?) була запропонована як домашнє завдання після першої лабораторної роботи в комп’ютерному класі. Перед наступним заняттям учні почали порівнювати отримані результати, вчитель вирішив використати цю ідею. При виконані другої лабораторної роботи діти використовували кожен свої статистичні дані. Потім вчителем було запропоновано зібрати та скласти всі результати в один. На уроці були присутні 25 учнів. На дошці зобразили таблицю 2.28

Таблиця 2.28

Потім її заповнили та отримали середній результат для 25 досліджень. У більшості випадків він співпав з результатами досліджень.

Під час проведення експериментального дослідження виникли деякі методичні рекомендації:

1. У цілях вдосконалення навчання математики доцільною є подальша розробка нових методик викладання розділів, що вводяться в зміст шкільної освіти.
2. В процесі цілеспрямованого навчання учнів розв’язанню задач, вчити їх спостерігати, користуватися аналогією, індукцією, порівняннями й робити відповідні висновки.
3. Необхідно враховувати індивідуальні особливості школярів, диференціацію пізнавальних процесів в кожного з них, використовуючи завдання різноманітного типу.

Після проведення тематичного оцінювання отримали такі результати, як в таблиці 2.29

Таблиця 2.29

Аналіз результатів експерименту дає підставу зробити такі висновки: дана методика може бути реалізована в загальноосвітній школі, вона дозволяє підвищити якість навчання при вивченні вивчення елементів стохастики в 9-х класах з поглибленим вивченням математики.

Все вищезазначене є підставою для підтвердження гіпотези дослідження.

ВИСНОВКИ ДО ДРУГОГО РОЗДІЛУ

 Введення імовірнісно-статистичної лінії до шкільного курсу математики суттєво підвищує прикладну спрямованість навчання математики. З’являється змога навіть за допомогою невеликого математичного апарату, якім оволодіватимуть учні, та імовірнісного мислення, яке в них формуватиметься, розв’язувати задачі, які мають громадську цінність. Але цей процес супроводжується складнощами. Одною з проблем є розробка якісного навчально-методичного забезпечення, яке б змістовно допомогло вчителям математики та підвищило рівень навчання.

Заняття з математики у відповідно оснащеному досконалими технічними засобами класі, з використанням педагогічних програмних засобів навчання – це один зі способів підвищити у учнів інтерес до навчання, урізноманітнити уроки та полегшити як учительську, так і учнівську роботу.

При викладанні початків теорії ймовірностей доцільно використовувати для аналізу статистичних закономірностей педагогічний програмний засіб GRAN1, рекомендований Міністерством освіти і науки України. Але необхідно раціонально розробити поурочний план та підібрати відповідні задачі.

Аналіз результатів апробації експериментальної методики дає підставу стверджувати, що її реалізація в загальноосвітній школі допоможе вчителям при викладанні початків теорії ймовірностей в одинадцятих класах з поглибленим вивченням математики та дасть змогу підвищити рівень навчання.