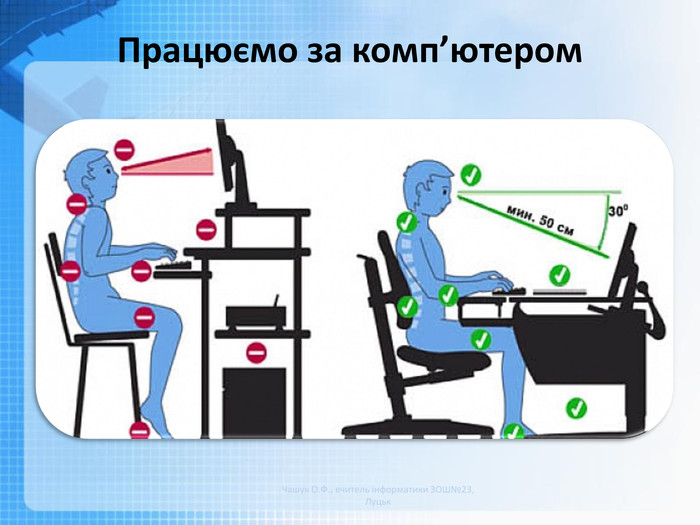
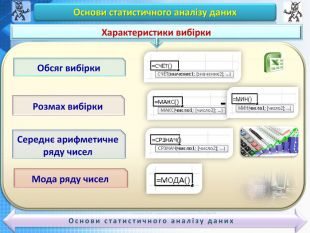
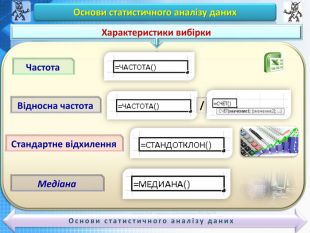
Основи статистичного аналізу даних. Ряди даних. Обчислення основних статистичних характеристик вибірки. Практична робота «Обчислення основних статистичних характеристик вибірки»

Основи статистичного аналізу даних. Ряди даних. Обчислення основних статистичних характеристик вибірки. Практична робота «Обчислення основних статистичних характеристик вибірки».

Актуалізація знань

1. Як обчислити середнє арифметичне кількох чисел? Для чого воно використовується? Наведіть приклади.

2. Що таке ряди даних у табличному процесорі? Наведіть приклади.

3. З якою метою проводять опитування? У яких опитуваннях ви брали участь?

ВИБІРКА І РЯДИ ДАНИХ

Вам уже відомо з курсу алгебри 9-го класу, що в багатьох дослідженнях для аналізу даних, установлення певних закономірностей, формулювання висновку, надання рекомендацій, прогнозування тощо потрібно використати багато даних. Ви знаєте, що методи отримання, опрацювання й аналізу даних, які характеризують масові явища, вивчає наука статистика (лат. status — стан).

Так, наприклад, для аналізу тенденцій змінення маси учнів 10-х класів України за останні роки, ризику серцевих захворювань людей певного віку на планеті, популярності продуктів харчування серед населення певного регіону потрібно проаналізувати сотні тисяч або навіть мільйони даних.

Зрозуміло, що провести зважування, вивчити історії хвороб, провести анкетування сотень тисяч або навіть мільйонів людей практично неможливо. Тому для аналізу створюють певну вибірку об’єктів дослідження, тобто з усієї множини об’єктів дослідження відбирають певну кількість і на ній проводять дослідження. Чим більше така вибірка, тим точніше буде проведено аналіз і зроблено відповідні висновки. Тобто вибірка повинна бути масовою.

Але не тільки кількість даних у вибірці визначає рівень точності аналізу і висновків. Так, у першому і другому з наведених вище прикладів доцільно вибирати людей різних регіонів і різної статі, а у третьому — людей різного віку. Кажуть, що вибірка даних має бути репрезентативною (франц. representatif — показовий, характерний, типовий).

Дані, отримані з дослідженої вибірки, найчастіше заносять у таблицю. Така форма подання даних з вибірки зручна для їх аналізу та прогнозів. Дані з кожного рядка і стовпця такої таблиці утворюють ряди даних.

Довідничок. Тенденція

Тенденція — це напрям розвитку, схильність, спрямованість.

Розглянемо кілька прикладів вибірок і рядів даних.

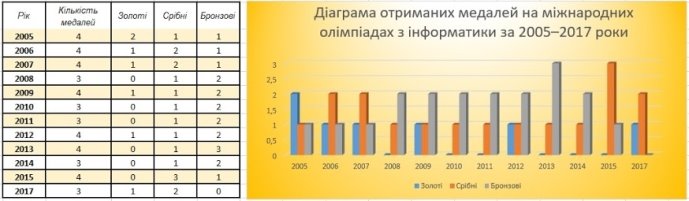
У таблиці подано результати виступів команди учнів України на міжнародних олімпіадах з інформатики з 2005 по 2017 рік. Тут вибіркою є вказані в таблиці роки, а рядами даних — загальна кількість медалей у ці роки, а також кількість золотих, срібних і бронзових медалей у вказані роки.

Зауважимо, що Україна бере участь у таких олімпіадах, починаючи з 1992 року. Команда кожної країни складається із чотирьох учнів. У 2016 році команда України не брала участі у такій олімпіаді.

За цими рядами даних або за деякими з них можна побудувати графіки або діаграми і візуалізувати їх, використовуючи, наприклад, табличний процесор.

Результати виступу команди учнів України на міжнародних олімпіадах з інформатики за 2005–2017 роки

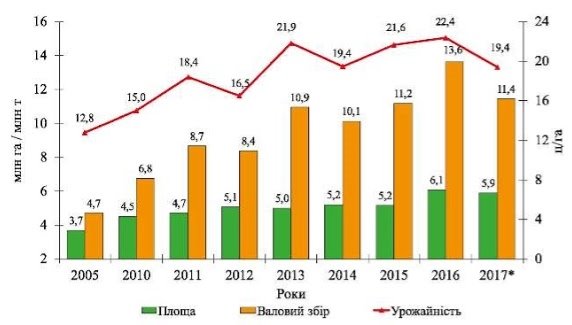
На малюнку подано діаграму динаміки посівних площ соняшнику в Україні в 1998–2015 роках і графік врожайності соняшнику в Україні за ці роки. Тут вибіркою є 2005–2017 роки, а рядами даних — посівні площі та врожайність соняшнику в ці роки.

Як приклад розглянемо роботу синоптичної служби. Синоптична служба збирає і зберігає дані про температуру, опади, атмосферний тиск та інші показники вже понад 160 років.

Для прогнозування температури та ймовірності опадів у Львові в першій декаді червня наступного року для проведення екскурсії потрібно вибрати відповідні дані, наприклад, за останні 10–15 років саме про Львів і саме про першу декаду червня, проаналізувати отримані два ряди даних (про температуру і кількість опадів) і зробити відповідний прогноз погоди.

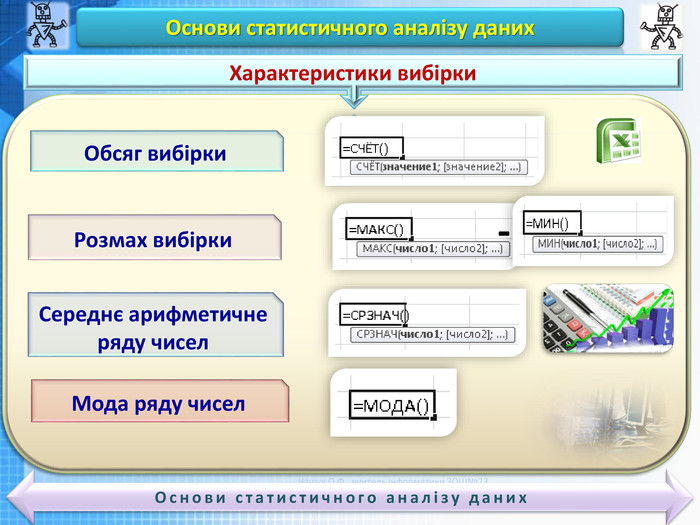
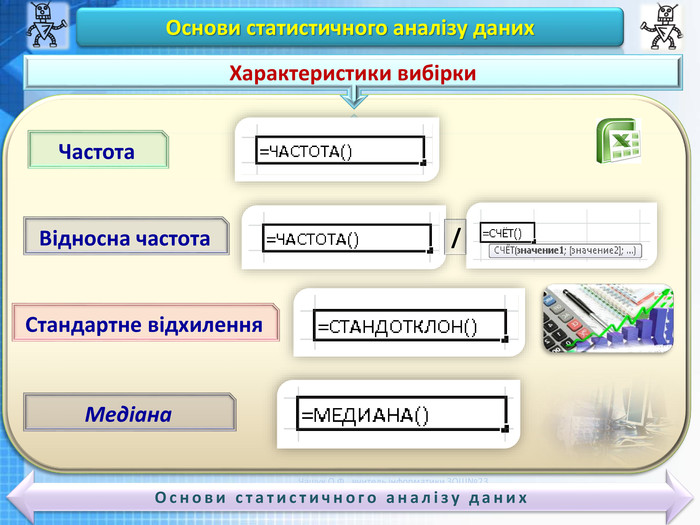
ДЕЯКІ СТАТИСТИЧНІ ХАРАКТЕРИСТИКИ РЯДУ ДАНИХ|

Розглянемо деякі статистичні характеристики ряду даних: середнє арифметичне. стандартне відхилення, мода і медіана.

Ви знаєте, що середнім арифметичним n чисел називається сума цих чисел, поділена на число n.

Так можна знайти середнє арифметичне врожайності соняшнику в Україні за 2006-2015 роки, використовуючи, наприклад, табличний процесор. Для обчислення середнього арифметичного в табличному процесорі можна використати відому вам функцію AVERAGE (англ. avеragе — середній), Нагадаємо, що аргументами цієї функції може бути діапазон клітинок, список клітинок, а також їх комбінації,наприклад AVERAGE(B2:D5; F4; E7). На малюнку 2,8 наведено приклад обчислення середньої врод-кайності соняшнику за 2006-2015 роки і формулу для її обчислення =AVERAGE(C3:C12).

Обчислене в наведеному прикладі середнє арифметичне визначає,яка б була врожайність кожного року (1.67 T/ra), якшо вона щороку була б однаковою. Аналогічно середнє арифметичне будь-якого ряду даних визначає, які б були значення в цьому ряді, якщо б вони всі були однакові. Зазначимо, що не для всіх рядів даних середнє арифметичне є показовою характеристикою самого цього ряду.

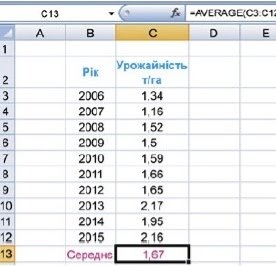
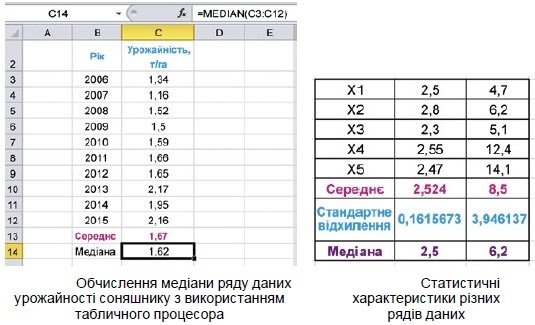
Обчислення середньої врожайності соняшнику за 2006-2015 роки

Наприклад, для ряду даних 2.5; 2.8; 2.3; 2.55; 2.47, у якому дані незначно відрізняються одне від одного, середнє арифметичне дорівнює 2.524, що незначно відрізняється від усіх членів цього ряду, а значить, достатньо показово характеризує весь цей ряд даних. А для ряду 4.7; 6.2; 5.1; 12.4; 14.1, у якому дані значно відрізняються одне від одного, середнє арифметичне дорівнює 8,5, що значно відрізняється від усіх членів цього ряду, а значить, недостатньо показово характеризує весь цей ряд даних.

Для визначення, наскільки показово середнє арифметичне ряду даних характеризує весь ряд даних, можна використати таку характеристику ряду даних, як стандартне відхилення. Стандартно відхилення характеризує, наскільки широко розташовані значення ряду даних відносно їх середнього арифметичного.

Стандартне відхилення обчислюється за формулою:

Обчислення основних статистичних характеристик вибірки засобами електронного процесора

Пригадайте можливості електронного процесора. Наведіть приклади використання автоматизованого опрацювання табличних даних.

Розглянемо, як можна використовувати програмний засіб MS Excel для обчислення статистичних даних на прикладі.

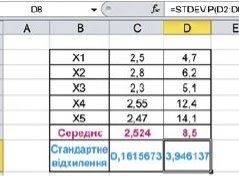
Очевидно, що середнє арифметичне першого ряду даних менше відрізняється від усіх членів ряду даних, а значить, більш показово характеризує весь цей ряд даних.

А середнє арифметичне другого ряду даних більше відрізняється від усіх членів ряду даних, а значить, менш показово характеризує весь цей ряд даних.

Автоматизувати обчислення стандартного відхилення в табличному процесорі можна, використавши функцію STDEV.P (англ. standard deviarion — стандартне відхилення) (для версії нижче 2010 — STDEVP).

Ще однією характеристикою ряду даних є мода.

Мода — це значення в ряді даних, яке повторюється найчастіше. Таке значення є показовим, наприклад, під час дослідження цін на ринку (ціна, яка трапляється найчастіше), під час дослідження попиту взуття, одягу (розміри, які купують найбільше) та ін.

У розглянутому вище прикладі мода кількостей медалей, які вибороло учнівство України на міжнародних олімпіадах з інформатики за 2005-2017 роки, дорівнює 4 (тому, що найчастіше в ці роки команда нашої країни завойовувала 4 медалі), мода кількостей золотих медалей – 0, мода кількостей срібних медалей – l, мода кількостей бронзових медалей - 2.

Якщо в ряді даних два або більше значень повторюються найбільшу кількість разів, то кожне з них вважається модою ряду даних. Так, наприклад, у ряді даних 2, 3, З, 2, 1 модою є і число 2, і число 3.

У табличному процесорі є спеціальна функція для обчислення моди ряду даних. Обчислення стандартного відхилення в табличному процесорі якщо вона одна – MODE.SNGL (англ. mode single — мода одинарна). Аргументами цієї функцції може бути діапазон клітинок, список клітинок. а також їх комбінації, наприклад AIODE.SNGL(B2:D5; F4; E7).

На малюнку наведено приклад обчислення моди для кількостей завойованих медалей і формула для її обчислення: =MODE.SNGL(E6:E17).

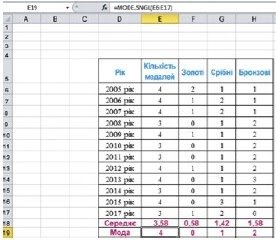
Обчислення моди в Excel, якщо вона єдина

Розглянемо ще одну характеристику ряду даних - медіану.

Медіаною впорядкованого ряду даних називається значення, яке поділяє ряд даних на дві рівні частини, тобто зліва і справа від цього значення знаходиться однакова кількість членів упорядкованого ряду даних.

Якщо у впорядкованому ряді даних непарна кількість членів, то медіана такого ряду даних дорівнює значенню його середнього члена, а якщо в такому ряді даних парна кількість членів, то його медіана обчислюється як середнє арифметичне значень двох середніх членів.

Наприклад. для ряду даних 2; З; 5; б; 7 медіана дорівнює 5, для ряду даних 2; З; 5; б: 7; 9 медіана дорівнює (5 + 6) :2 = 5,5. а для ряду даних 2; 2; 4: 4: 4; 5; 6 медіана дорівнює 4.

Медіана використовується. наприклад. для визначення місця побудови шкіл, дитячих садочків, магазинів. підприємств побуту тощо. Потрібно визначити ряд відстаней, які мають подолати мешканці певної місцевості до цього закладу, і побудувати його в точці. яка визначається медіаною цього ряду.

У табличному процесорі є спеціальна функція для обчислення медіани ряду даних - MEDIAN (англ. median— середній). Аргументами цієї функції може бути діапазон клітинок, список клітинок, а також їх комбінації, наприклад MEDIAN(В2:D5; F4: E7).

На малюнку наведено приклад обчислення медіани ряду даних урожайності соняшнику з використанням табличного процесора за формулою =MEDIAN(С3:С12).

Звертаємо вашу увагу, що в електронній таблиці для знаходження медіани ряд даних не обов'язково має бути впорядкований. Табличний процесор спочатку впорядковує ряд даних, а потім визначає його медіану.

Зазначимо, що коли члени ряду даних незначно відрізняються одне від одного, то і середнє арифметичне, і медіана більш показово характеризують весь цей ряд.

А якщо члени ряду даних значно відрізняються одне від одного, то медіана більш показово характеризує весь цей ряд даних, ніж середнє арифметичне.

Оскільки найбільш поширені функції винесено окремо на стрічці Формули та на стрічці Основне, скористаємося останньою для обчислення значень функцій Середнє арифметичне, Максимум та Мінімум.

Розглянемо детально, як використовувати функції статистичного аналізу в MS Excel.

Група Статистичні функції знаходиться в групі Інші функції, ця сама група відображається у вікні, яке викликається командою Вставити функцію.

Практична робота

Для розуміння, як використовувати функції підрахунку статистичних характеристик, виконайте практичну роботу.

Увага! Під час роботи з комп'ютером дотримуйтеся вимог безпеки життєдіяльності та санітарно-технічних норм.

Задача На шкільних змаганнях з легкої атлетики проводять два півфінальних забіги. У фінал проходить половина учасників кожного півфіналу. У таблиці наведено результати учасників одного з півфіналів. Обчисліть середнє арифметичне, стандартне відхилення, моду й медіану наведеного ряду даних.

Для цього:

1. Запустіть табличний процесор.

2. Заповніть діапазони клітинок В2:В15 і C2:C11 відповідно до зразка.

3. Уведіть у клітинку C12 формулу =AVERAGE(C2:C11).

4. Уведіть у клітинку C13 формулу =STDEV.P(C2:C11).

5. Уведіть у клітинку C14 формулу =МODE.SNGL(C2:C11).

6. Уведіть у клітинку С15 формулу =МEDIAN(C2:C11).

7. Збережіть електронну книгу у вашій папці у файлі з іменем вправа 2.2.

8. Запишіть у зошит пояснення. яка з отриманих характеристик указаного ряду даних визначить. хто з учасників цього півфіналу вийде у фінал.

9. Змініть 2-3 числа у клітинках C2:C11. Запишіть у зошит, у яких клітинках ви змінили значення і на які а також, як змінилися результати обчислень за формулами у клітинках C12: C15.

10 Закрийте вікно табличного процесора

Запитання для самоперевірки знань

1. Які групи функцій містять функції обчислення статистичних характеристик?

2. Яким сполученням клавіш користуються для підтвердження опрацювання даних масиву?

3. Які функції містить MS Excel для обчислення моди?

4. Чому для обчислення моди резервують більше однієї клітинки?

5. Як ви розумієте «інтервал значень» як аргумент функції ЧАСТОТА? Поясніть на прикладі.

6. Яке призначення статистичної характеристики відносної частоти? У якому форматі краще аналізувати вказану характеристику: у відсотковому чи ні?

Дайте відповіді на запитання

1) Що вивчає наука статистика? Наведіть приклади.

2) Яким вимогам має відповідати вибірка об’єктів дослідження? Поясніть кожну з них.

3) Шо таке ряд даних? Наведіть приклади.

4) Що характеризує середнє арифметичне ряду даних?

5) У яких випадках середнє арифметичне більш показово характеризує весь ряд даних, а у яких - менш показово?

6) Що таке стандартне відхилення ряду даних? Шо воно характеризує?

7) Що таке мода ряду даних? Що вона характеризує?

8) Що таке медіана ряду даних? Що вона характеризує?

9) У впорядкованому ряді чисел найбільше число збільшили на 5. Як зміняться значення середнього арифметичного, моди і медіани цього ряду? Відповідь поясніть.

Тренувальні вправи. Робота за ПК

1) Є ряд даних: 56,5; 27,9; 32,4; 59,23; 44,87; 41; 39,7; 49,98. Обчисліть середнє арифметичне стандартне відхилення моду й медіану для цього ряду даних. Електронну книгу збережіть у вашій папці у файлі з іменем завдання 2.2.1.

2) Є відомості про зріст кожного учня та учениці вашого класу. Обчисліть ceреднє арифметичне, стандартне відхилення, моду й медіану для рядів даних таких вибірок: половина хлопців вашого класу, половина дівчат вашого класу, усі хлопці вашого класу, усі дівчата вашого класу. Проаналізуйте отримані результати і запишіть висновки. Електронну книгу збережіть у файлі з іменем Завдання 2.2.2.

3) Є відомості про масу кожного учня та учениці вашого класу. Обчисліть середнє арифметичне, стандартне відхилення, моду й медіану для рядів даних таких вибірок: третина хлопців вашого класу, третина дівчат вашого класу, усі хлопці вашого класу, усі дівчата вашого класу. Проаналізуйте отримані результати і запишіть висновки. Електронну книгу збережіть у вашій папці у файлі з іменем завдання 2.2.3.

4) Складіть таблицю кількостей опадів у вашому регіоні за кожний місяць минулого року. Обчисліть середнє арифметичне, стандартне відхилення, моду і медіану для цього ряду даних. Проаналізуйте отримані результати і запишіть висновки. Електронну книгу збережіть у вашій папці у файлі з іменем завдання 2. 2. 4.

5) Cкладіть таблицю з ваших оцінок за минулий навчальний рік. Обчисліть ceреднє арифметичне, стандартне відхилення моду й медіану для цього ряду даних. Проаналізуйте отримані результати і запишіть висновки. Електронну книгу збережіть у вашій папці у файлі з іменем завдання 2. 2. 5.

6) Проведіть опитування серед учнів і учениць 10- х класів вашого навчального закладу (якими видами спорту займаються, на яких музичних інструментах грають, які кінофільми люблять дивитися, яку літературу люблять читати тощо). Для кожного опитування складіть таблиці. Обчисліть статистичні характеристики отриманих рядів даних. Проаналізуйте отримані результати і запишіть висновки. Електронну книгу збережіть у вашій папці у файлі з іменем завдання 2.2.6.

 

Microsoft Excel

“Основи статистичного аналізу”

Вправа 1. Порівняння двох вибірок

Туристична фірма, що реалізує путівки у семи містах країни, провела рекламну кампанію. У таблиці наведено дані про кількість путівок, проданих протягом тижня до проведення рекламної кампанії та протягом тижня після неї. Потрібно, обчисливши характеристики центру та варіації розподілу, порівняти дві вибірки та зробити висновки щодо впливу рекламної кампанії на обсяги продажу путівок.

1.                Створіть у новій електронній книзі аркуш з іменем Вправа 9-1, а у ньому таблицю за зразком, наведеним на рис. 1, та збережіть документ під іменем Вправа 1.xlsх.

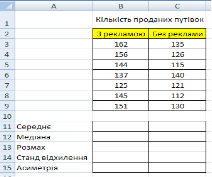
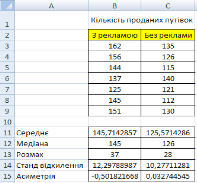
Рис. 1. Дані про діяльність турагенства Рис. 2. Статистичні характеристики вибірки

2. Такий показник, як мода, обчислювати недоцільно, оскільки відомості про те, яка кількість проданих путівок траплялася найчастіше, навряд чи можна якось використати. Тож обчисліть середнє значення для обох вибірок,

а) Скориставшись кнопкою Вставка функції, введіть у клітинку В11 формулу =АVERAGE(ВЗ:В9). У цій клітинці буде обчислено середнє значення для стовпця 3 рекламою; воно дорівнює 145,71.

б) Скопіюйте формулу з клітинки В11 у клітинку С12. У ній буде обчислено середнє значення для стовпця Без реклами.

3. Аналогічним чином у діапазоні В12:С15 обчисліть для обох вибірок медіану, розмах, стандартне відхилення та асиметрію. Для обчислення розмаху скористайтеся функціями МІМ та МАХ, оскільки розмах — це різниця найбільшого та найменшого елемента вибірки. Ви маєте отримати такі результати, як на рис. 2. Збережіть таблицю.

4. Зробіть висновки. Середнє значення та медіана вибірки 3 рекламою значно перевищують відповідні показники вибірки Без реклами, що свідчить про позитивний вплив рекламної кампанії на обсяги продажу путівок. З іншого боку, після рекламної кампанії збільшилися розмах вибірки та стандартне відхилення. Це означає, що обсяги продажу путівок у різних містах стали більше різнитися між собою, стали менш однорідними та передбачуваними. Можливо, такий результат обумовлений тим, що якість рекламної кампанії в різних містах була різною або жителі різних міст по-різному на неї відреагували. Значення асиметрії до рекламної кампанії майже дорівнювало нулю. Це є свідченням того, що в містах, де обсяги продажів були великими, вони приблизно настільки ж перевищували середній обсяг, наскільки маленькі обсяги продажів були менші за нього. Після рекламної кампанії ми отримали суттєву від'ємну асиметрію вибірки. Це означає, що в деяких містах обсяги продажів стали значно меншими за середні, в той час як великі обсяги перевищують середню величину менш істотно. Інакше кажучи, незважаючи на загальний позитивний вплив рекламної кампанії, у деяких містах вона фактично провалилася.

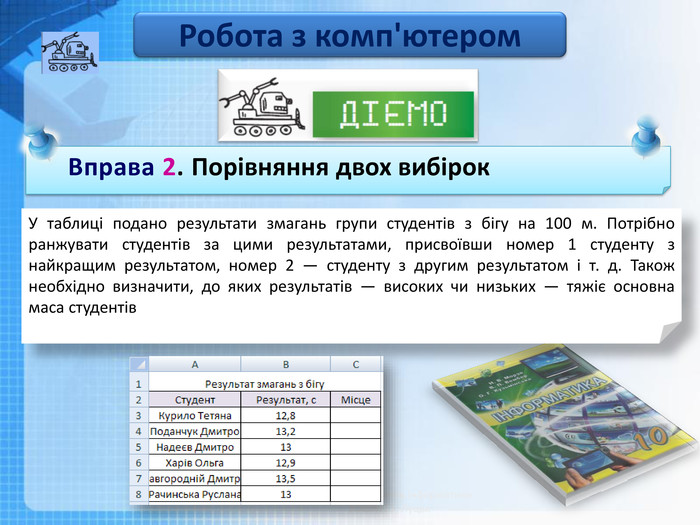
Вправа 2. Ранжування вибірки

У таблиці, наведеній на рис. 3, подано результати змагань групи студентів з бігу на 100 м. Потрібно ранжувати студентів за цими результатами, присвоївши номер 1 студенту з найкращим резуль­татом, номер 2 — студенту з другим результатом і т. д. Також необхідно визначити, до яких результатів — високих чи низьких — тяжіє основна маса студентів.

1.                Відкрийте файл Вправа 1-2.xlsх та додайте аркуш із іменем Вправа 9-2, на якому створіть таку таблицю, як на рис. 3.

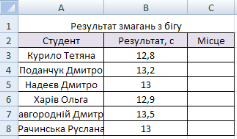
Рис. 3. Таблиця з вихідними даними

2.                Для ранжування студентів скористайтеся функцією РАНГ, яку потрібно ввести у клітинку СЗ і скопіювати у діапазон С4:С42. Формула у клітинці СЗ має бути такою: =РАНГ(В3;В$3:В$8;1). Клітинка С3 містить число, яке ранжується, В$3:В$8 — діапазон усіх результатів. Зверніть увагу, що номери стовпців у діапазоні результатів фіксовані, а посилання на клітинку, ранг якої обчислюється, відносне. Тому після копіювання цієї формули значення, ранг якого обчислюється, змінюватиметься, а весь діапазон значень залишатиметься тим самим. Місця студентів у змаганнях з бігу мають відобразитися у стовпці С.
3.                Щоб визначити, до яких значень — високих чи низьких — тяжіють результати основної маси студентів, варто обчислити асиметрію вибірки. Отже, уведіть у будь-яку клітинку поза межами таблиці формулу =СКОС(В3:В8), і буде обчислено асиметрію розподілу результатів змагань з бігу. Вона дорівнює приблизно —1,1. Знайдіть найкращий результат (це студент з рангом 1), він дорівнює 12,8 с. Зменште його до 10 с, і асиметрія стане меншою, оскільки найкращий результат став ще рідкіснішим.