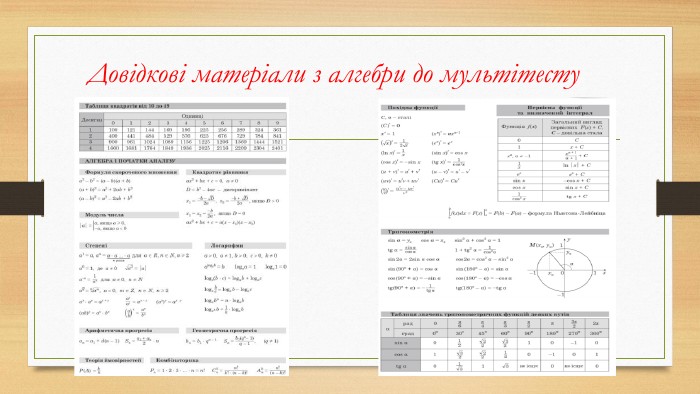
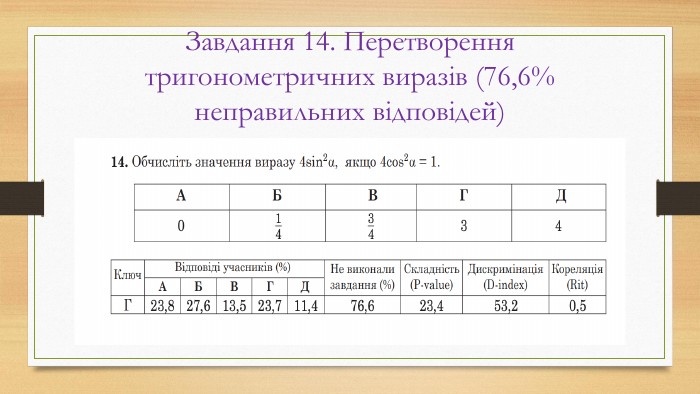
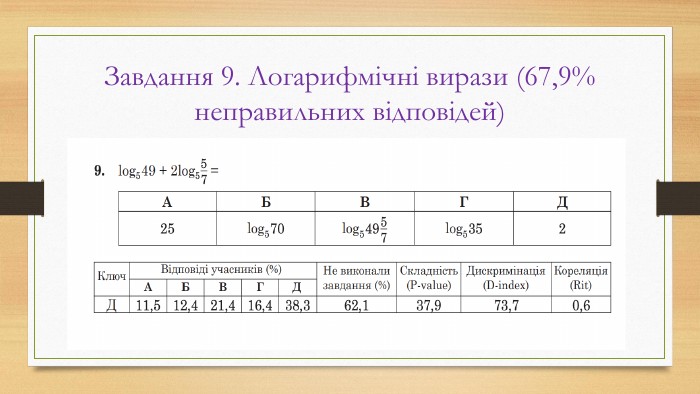
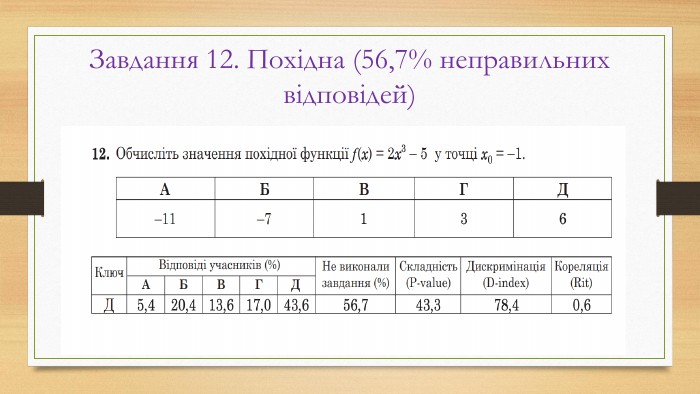
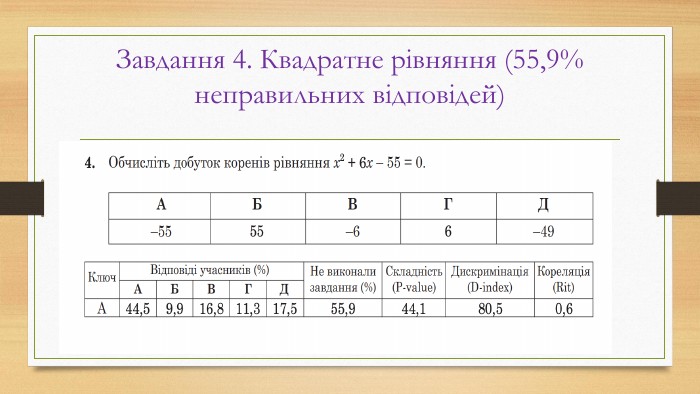
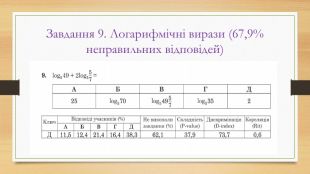
Основні помилки НМТ з математики у 2022 році
Про матеріал
Матеріал призначений для учнів 11 класів , які готуються до НМТ з математики у 2023 році Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку