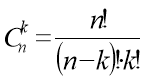Основні поняття комбінаторики. Розміщення, перестановки, комбінації.

Тема.  Основні поняття комбінаторики. Розміщення, перестановки, комбінації.

Спеціальність: «Кухар. Кондитер».

Мета уроку:

Навчальна: ознайомити учнів з елементами комбінаторики, комбінаторними правилами суми та добутку, з формулами для обчислення числа перестановок, розміщень і комбінацій; учити використовувати ці формули під час розв'язування задач; дати схему розв'язування комбінаторних задач;

Розвиваюча: розвивати в учнів пізнавальний інтерес, логічне мислення, уміння використовувати навички й уміння в нових ситуаціях; формувати навички контролю та самоконтролю; прищеплювати інтерес до вивчення математики.

Виховна: виховувати відповідальність та зібраність до навчального процесу; сприяти розширенню кругозору учнів; виховувати ерудованість, математичну грамотність, наполегливість та любов до обраної професії.

Тип уроку: урок засвоєння нових знань.

Міжпредметні зв’язки: основи галузевої економіки та підприємництва, організація виробництва та обслуговування.

Очікувані результати: учні повинні знати правило суми та правило добутку, означення розміщення, перестановки, комбінації та формули для обчислення їх кількості;  вміти розрізняти сполуки і знаходити їх кількість за відповідними формулами; розв’язувати задачі, що передбачають використання комбінаторних правил суми та добутку; наводити приклади застосування правил комбінаторики.

ХІД УРОКУ

І. Організаційний момент

Перевірка готовності учнів до уроку. Фіксація відсутніх на уроці. Налаштування на роботу.

ІІ. Мотивація навчальної діяльності учнів

Сьогодні на уроці ми будемо вивчати основні поняття комбінаторики і покажемо важливість теми у математиці та у вашій професії.

Створення проблемної ситуації.

Уявіть ситуацію:

На роботу у новий великий ресторан прийшли працювати 15 чоловік. Директору треба вибрати шеф-кухара та су-шефа. Скількома способами це можна зробити?

Як ви вважаєте, що для вирішення даної ситуації нам необхідно знати?

Після обговорення ситуації, учні доходять висновку, що, для того щоб дати відповідь на запитання задачі треба знайти всі можливі варіанти, а їх дуже багато.

Відповідь можна надати швидко, якщо знати формулу, з якою ми ознайомимося сьогодні на уроці. Адже, недарма ще французький  письменник Анатоль Франс говорив, що недостатньо знати, необхідно також вміти застосовувати.

ІІІ. Актуалізація опорних знань. Перевірка домашнього завдання.

Перш ніж розпочати вивчення нового матеріалу давайте пригадаємо вивчений матеріал, розгадавши кросворд за посиланням https://onlinetestpad.com/f4fhnt7ht53xm (платформа Online Test Pad).

З допомогою слів-підказок вгадати ключове слово кросворду.

ПО ВЕРТИКАЛІ:

1.     Діаграми Ейлера-Венна.
2.     Будь-яке явище, що може відбутися або не відбутися у результаті експерименту.
3.     Об’єкти множини.
4.     Умови, в результаті яких відбувається ( чи не відбувається) подія.
5.     Відношення числа подій, які сприяють виконанню даної події, до загальної кількості подій простору елементарних подій.
6.     Подія, яка внаслідок даного випробування не може відбутися.
7.     Подія, яка внаслідок даного випробування обов’язково відбудеться.
8.     Скільки відсотків становить вірогідна подія.
9.     Подія, яка може відбутися або не відбутися під час даного випробування.
10. Множина, в якій порядок елементів важливий.
11. Випробування – підкидання грального…
12. Відомий математик, пов'язаний з терією ймовірностей.

 

			4
				5						11		13
		3				7		9	10
	2						8
1					6						12

Відповіді до кросворду.

ПО ВЕРТИКАЛІ:

1.               Круги.
2.               Подія.
3.               Елементи.
4.               Випробування.
5.               Ймовірність.
6.               Неможлива.
7.               Випадкова.
8.               Сто.
9.               Вірогідна.
10.          Впорядковані.
11.          Множина.
12.          .Кубика.
13.          Ферма.

ПО ГОРИЗОНТАЛІ: КОМБІНАТОРИКА.

IV. Сприйняття та усвідомлення нового матеріалу.

Комбінаторика – це розділ математики, що вивчає розташування об'єктів у відповідності з спеціальними правилами і методи підрахунку числа всіх можливих способів, якими ці розташування можуть бути зроблені.

Методи комбінаторики відіграють важливу роль при обчисленні ймовірностей різних подій, пов'язаних з експериментами, що мають скінченне число результатів випробувань.

Сформулюємо основні поняття комбінаторики.

Правило суми. Якщо деякий вибір А можна здійснити n різними способами, а деякий інший вибір В можна здійснити m способами, то вибір або A, або В можна здійснити n+m способами.

Приклад. З Києва до Кропивницького веде n різних доріг через Кагарлик і m доріг через Бориспіль. Якою кількістю різних доріг можна доїхати з Києва до Кропивницького?

Розв'язання.  3 Києва до Кропивницького можна доїхати, вибравши одну з n+m можливих доріг. Тому загальна кількість доріг рівна n + m.

Правило множення. Якщо деякий вибір А можна здійснити n різними способами, а для кожного з цих способів деякий інший вибір В можна здійснити m способами, то вибір А і В (у вказаному порядку) можна здійснити n•m способами.

Приклад. З Києва до Кропивницького веде m різних доріг, а з Кропивницького до Одеси - n доріг. Якою кількістю різних доріг можна здійснити подорож з Києва до Одеси через Кропивницький?

Розв’язання. Вибравши одну з m можливих доріг з Києва до Кропивницького, далі можна продовжити подорож  n способами. Тому загальна кількість доріг рівна n • m.

Поняття факторіала.

Факторіалом числа n, де n – ціле невід’ємне число, називається добуток усіх натуральних чисел від 1 до n.

Позначається n! (читається «ен факторіал»).

.

За означенням приймають .

Наприклад:  .

Дуже часто трапляються випадки коли треба спростити вираз в якому існують факторіали.

Наприклад: .

Комбінації (сполучення) з n по k.

Нехай Х - множина з n елементів. Довільну k-елементну підмножину Y множини X з n елементів називають комбінаціями з n по k. Порядок елементів в підмножині несуттєвий. Число сполучень з n по k позначається  .

Число сполучень з n елементів по k рівне

 

Приклад. Скільки карток „Спортлото" 5 із 36 треба заповнити, щоб серед них обов'язково одна була з п'ятьма вгаданими номерами?

Розв'язання. Оскільки порядок „викреслювання" не має значення, то мова йде про сполучення 5 з 36. Якщо одна картка буде відрізнятися від іншої хоча б одним викресленим номером, то перебравши усі сполучення по 5 з 36, отримаємо одну картку з п'ятьма вгаданими номерами.

Тобто число карток рівне

.

Відповідь: 376992 картки.

Впорядковані множини, перестановки.

Множину називають впорядкованою, якщо кожному елементу цієї множини поставлене у відповідність деяке число (номер елемента) від 1 до n, де n - кількість елементів множини, так, що різним елементам відповідають різні числа. Очевидно, кожну множину, що містить більше одного елемента, можна впорядкувати не єдиним способом. Впорядковані множини вважаються різними, якщо вони відрізняються порядком розташування елементів. Перестановками називають сукупність впорядкованих множин, які можна отримати із п елементів.

Число перестановок з n елементів позначають через .

Число всіх можливих перестановок із n елементів дорівнює добутку всіх натуральних чисел від 1 до n: .

Приклад. В кондитерський магазин завезли 6 видів тортів. Скількома способами їх можна розставити на вітрині.

Розв'язання. Оскільки в цьому випадку одна комбінація відрізняється від іншої тільки порядком заданих елементів, то мова йде про перестановки. Кількість різних способів розставити торти на вітрині дорівнює числу перестановок із шести елементів: .

Відповідь: 720 способів.

Розміщення з n по k. Розглянемо впорядковані підмножини даної множини Х. Саму множину Х вважаємо невпорядкованою, тому кожну її підмножину можна впорядкувати яким-небудь можливим способом. Число всіх k-елементних підмножин множини Х рівне . Кожну підмножину можна впорядкувати k! способами. Таким чином, отримаємо всі впорядковані k-елементні підмножини множини Х і їх число рівне

.

Число впорядкованих к-елементних  підмножин множини з n елементів рівне

 

Впорядковані к-елементні підмножини множини з n елементів називаються розміщеннями з n елементів по k. Розміщення з n по k відрізняються складом елементів або їх порядком.

Приклад. Припустимо, що мобільний телефонний номер семизначний (код оператора не враховується). Скільки існує номерів, в яких не повторюється ні одна цифра? (номери можуть починатися з 0).

Розв'язання. Відомо, що мобільний телефонний номер складається із різної послідовності семи цифр. При складанні телефонного номера із 10 цифр вибирають 7. Один номер відрізняється від іншого або різними цифрами, або їх порядком.

Таким чином, кількість телефонних номерів, у яких цифри не повторюються, дорівнює числу розміщень із 10 по 7:

.

Відповідь: 604800 номерів.

Всі формули можна звести в одну таблицю

1. ВИБІР ПРАВИЛА
ПРАВИЛО СУМИ		ПРАВИЛО ДОБУТКУ
Якщо елемент А можна вибрати n способами, а елемент В – m способами, то А або В можна вибрати m+n способами		Якщо елемент А можна вибрати n способами, а для кожного з цих способів деякий елемент В – m способами, то А і В можна вибрати m∙n способами
2. ВИБІР ФОРМУЛИ
Чи враховується порядок розміщення елементів?
ТАК		НІ
Чи всі елементи входять до сполучення?
ТАК	НІ
ПЕРЕСТАНОВКИ	РОЗМІЩЕННЯ	КОМБІНАЦІЇ

V. Осмислення і закріплення знань учнів.

Вирішення проблемної ситуації.

На роботу у новий великий ресторан прийшли працювати 15 чоловік. Директору треба вибрати шеф-кухара та су-шефа. Скількома способами це можна зробити?

Розв'язання. Шеф-кухарем може стати будь-хто з 15 чоловік. Після обрання шеф-кухара на роль його заступника су-шефа можуть претендувати 14 чоловік, які залишилися. Таким чином, всього є 15∙14 = 210 різних варіантів виборів, тому що вибір шеф-кухара обмежує коло претендентів на роль заступника: шеф-кухар не може бути су-шефом. Таким чином, вибори шеф-кухара та його заступника су-шефа не є незалежними.

Розв’язування задач

Задача 1. На тарілці лежать 6 яблук і 9 груш. Скількома способами можна взяти один фрукт?

Розв 'язання.

Очевидно, що в задачі треба використати правило суми, тому що можна обрати яблуко або грушу.

Відповідь: 15 способів.

 

Задача 2. Маємо набір з 10 різних цифр і 5 різних букв. Скількома способами можна обрати набір з однієї цифри і однієї букви?

Розв 'язання.

Так як необхідно вибрати одну цифру і одну букву, то, звісно, що в задачі використовується правило множення.

Отримаємо: .

Відповідь: 50 способів.

 

Задача 3. Скільки різних слів можна отримати, переставляючи літери слова "ВЕКТОР"?

Розв'язання.

Оскільки всі літери слова різні, то всього можна отримати 6!=720.

Відповідь: 720 слів.

 

Задача 4. В країні 20 міст, кожні два з яких з'єднані авіалінією. Скільки авіаліній в цій країні?

Розв'язання.

Кожна авіалінія з'єднує два міста. За перше місто можна взяти будь-яке з 20 міст (місто А), за друге – будь-яке з 19, які залишилися (місто В). Перемноживши ці числа, дістаємо 20∙19 = 380. Але при цьому підрахунку кожна авіалінія врахована двічі (перший раз, коли за перше місто було вибрано місто А, друге – місто В, а другий раз – навпаки). Таким чином, кількість авіаліній дорівнює 380:2 = 190. 

Відповідь: 190 авіаліній.

 

Задача 5.  Скількома способами можна розставити на полиці 5 різних книжок?

Розв’язання.

Розв’яжемо задачу через формули комбінаторики.

Для цього дамо відповідь на 2 запитання з таблиці:

1) Чи враховується порядок розміщення елементів? Так.

2) Чи всі елементи входять до сполуки? Так.

В такому разі обчислюємо перестановки 5 книг

 Відповідь: 120 способів.

 

Задача 6. Скількома способами можна подати страви дитячого святкового меню складеного з 5 страв, якщо в кафе пропонують на вибір 10 різних страв?

Розв’язання.

Перевіряємо умову: 1) Чи враховується порядок розміщення елементів? Так, тому що всі страви різні.

2) Чи всі елементи входять до сполуки? Ні, оскільки маємо 10 різних страв і всього 5 треба вибрати. Тому застосовуємо розміщення з 10 по 5

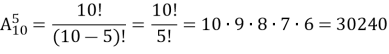Відповідь: 30240 способів.

 

Задача 7. Скількома способами можна з 20 чоловік призначити двох чергових в їдальні з однаковими обов’язками?

Розв’язання.

Всі хто хотів робити по аналогії з попередніми завданнями отримають відповідь 20•19=380, що є неправильним.

А все тому, що маємо підказку «чергові з однаковими обов’язками», тобто Андрій, Василь чи Василь, Андрій є одним і тим самим, однією комбінацією.

А на перше питання «Чи враховується порядок розміщення елементів?» маємо відповідь «Ні». Тому тут слід використовувати формулу комбінацій з 20 чоловік по 2

Відповідь: 190 способів.

 

Задача 8. (задача підвищеної складності).

Із 3 кухарів та 5 офіціантів треба створити команду з 4 чоловік, в яку має обов’язково входити хоча б один кухар.

Розв’язання.

Розглянемо різні випадки

1.               Можна взяти 1 кухара з 3, тобто комбінація з 3 по 1

 

і 3 офіціанта з 5, тобто комбінація з 5 по 3

.

Тоді використаємо правило множення, тому що треба і кухар і офіціанти. Отримаємо

2.               Можна взяти 2 кухара з 3, тобто комбінація з 3 по 2

 

і 2 офіціанта з 5, тобто комбінація з 5 по 2

.

Тоді знову треба використати правило множення, тому що треба і кухарі і офіціанти. Отримаємо .

3.               Можна взяти 3 кухара з 3, тобто комбінація з 3 по 3

 

і 1 офіціант з 5, тобто комбінація з 5 по 1

.

Використавши правило множення, отримаємо .

Тепер треба об’єднати всі три варіанти. Так як можливий один з трьох випадків, або перший, або другий, або третій, необхідно скористатися правилом суми. Тобто,

.

Відповідь: 65 способів.

 

Тестування за посиланням

https://wordwall.net/play/14358/369/277

(платформа Wordwall)

1.              Скількома способами можна розставити 6 книжок на полиці?
   1.               120;
   2.               6;
   3.               720;
   4.               24.
2.              Скільки 4-цифрових чисел можна скласти з цифр 2, 7, 8, 6 таким чином, щоб цифри не повторювались? 
   1.               24;
   2.               4;
   3.               120;
   4.               16.
3.              На столі лежать 6 яблук та 3 сливи. Скількома способами можна взяти 1 яблуко і 1 сливу?
   1.               6;
   2.               3;
   3.               9;
   4.               18.
4.              У групі туристів 16 осіб. Скількома способами можна сформувати з них групу з 3 туристів для екскурсії?
   1.               560;
   2.               1680;
   3.               48;
   4.               3360.
5.              Скільки існує варіантів розподілу 3 призових місць, якщо в конкурсі фахової майстерності беруть участь 25 учнів?
   1.               2300;
   2.               13800;
   3.               75;
   4.               125.
6.              В нову кав'ярню прийшли працювати 18 працівників. Скількома способами можна обрати адміністратора та його помічника?
   1.               4896;
   2.               36;
   3.               153;
   4.               306.
7.              Скількома способами можна обрати 4 блюда для обіду з меню, що складається з 19 страв?
   1.               76;
   2.               1938;
   3.               3876;
   4.               204.
8.              В групі навчається 21 учень. Скільки існує варіантів вибору 2 учнів для чергування?
   1.               630;
   2.               315;
   3.               42;
   4.               10.
9.              В ювелірну майстерню привезли 6 алмазів та 9 ізумрудів. Ювеліру замовили браслет в якому має бути 3 алмази і 5 ізумрудів. Скількома способами він може вибрати камені на браслет?
   1.               2520;
   2.               146;
   3.               20;
   4.               126.

Задача 9. (Додаткове завдання підвищеної складності).

Підприємство може надати роботу за однією спеціальністю чотирьом жінкам, за другою – шести чоловікам і за третьою – трьом робітникам незалежно від статі. Є 14 претендентів: 6 жінок і 8 чоловіків. Скількома способами можна заповнити вакантні місця?

VІ. Підбиття підсумків уроку.

Я дякую всім вам, дорогі учні за цікавий урок. Закінчити хочеться словами  видатного педагога сучасності Василя Сухомлинського «Математика вчить мислити й разом з тим вселяє віру в безмежні сили людського розуму. Вона виховує волю, характер».

Рефлексія.

Питання до всіх учнів:

• Cподобався вам урок?
• Що найбільше вам сподобалось?
• Що нового дізнались?
• З якими труднощами зустрілись?

VІІ. Домашнє завдання  

1.               Вивчити формули.
2.               Пройти тестування за QR_CODЕ (інтерактивна вправа на онлайн сервісі LearningApps)

3.               Розв’язати задачі.

1.  Скількома способами можна розмістити 10 відвідувачів кафе за одним столом біля якого 10 стільців?
2.  Скількома способами із 9 членів комісії можна вибрати голову, заступника і секретаря?
3.  В цеху на кондитерській фабриці працює 15 чоловік. Скількома способами можна обрати 5 кондитерів для роботи в першій зміні?
4.  Після успішного написання ЗНО з математики, п’ятеро щасливих учнів здійснили подорож до Чорного моря, замовивши для цього автомобіль з водієм на 5 пасажирських місць. Господар автомобіля запропонував їм такий відпочинок щороку і кожного разу сідати у той самий автомобіль по іншому. Після того, як усі способи будуть вичерпані, їх возитимуть безкоштовно. Через скільки років настане цей щасливий день?

4). Скласти та розв’язати задачу, що стосується професії, яку необхідно розв’язувати за допомогою комбінаторики.