Основні поняття теорії імовірності

Основні поняття теорії ймовірностей.

РЕБУС «ПОДІЯ»

ПОДІЯ Подія – це явище, про яке можна сказати, що воно відбувається чи не відбувається за певних умов. Події позначаються великими літерами латинського алфавіту: А, В, С … НАПРИКЛАД. Підкидаємо шестиграний гральний кубик. Визначаємо події: А {випало парне число очок}; В {випало число очок, кратне 3}; С {випало більше 4 очок}. Будь-яка подія відбувається внаслідок випробування (експерименту, досліду) 

Випробування (дослід) Випробування – це умови, в результаті яких відбувається (чи не відбувається) подія. Наприклад, випробування – підкидання кубика події: А – “поява 1 очка”, В – “поява 2 очок”, С – “поява 3 очок”, D – “поява 4 очок”, E – “поява 5 очок”, G – “поява 6 очок”. 

Приклади здача екзамена, спостереження за дорожньо -транспортними пригодами, вистріл з гвинтівки, підкидання грального кубика, хімічний експеримент, і т.п.

Розглянемо декілька прикладів випадкових експериментів, які розглядають в теорії імовірностей.

Дослід 1: Підкидання монети. Випробування – підкидання монети; події – монета впала «гербом» або «цифрою». 

Дослід 2: Підкидання кубика. Випробування – підкидання кубика; події – випало 1, 2, 3, 4, 5 або 6 очок (і інші). 

Дослід 3: Вибір перчаток. В коробці лежать 3 пари однакових перчаток. З неї, не дивлячись, виймають дві перчатки. «Завтра дньом – ясна погода». Тут настання дня – випробування, ясна погода – подія.   Дослід 4:

Виконання вправ Відокремте події і випробовування: а) тягнемо екзаменаційний білет, випадає білет № 13; б) дістаємо лампу з коробки, вона бракована; в) набираємо навмання телефонний номер і чуємо голос знайомого; г) відкриваємо поштову скриньку і знаходимо лист; д) стріляємо і влучаємо в ціль. 2. Наведіть свої приклади випробовувань і подій.

Типи подій ВІРОГІДНА НЕМОЖЛИВА ВИПАДКОВА ПОДІЯ

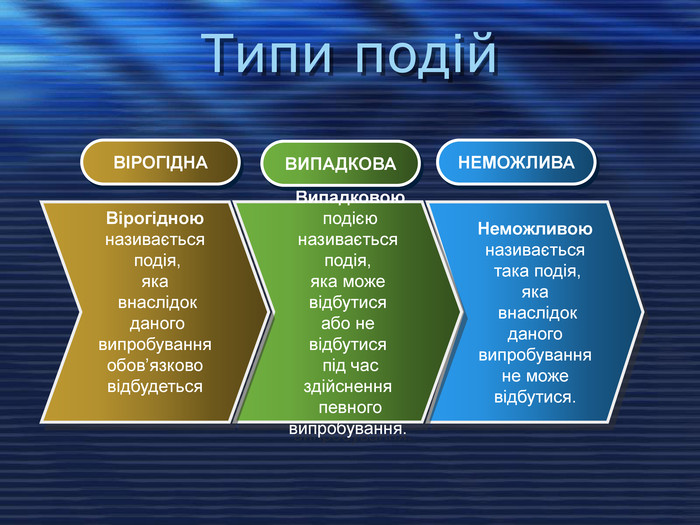
Типи подій Неможливою називається така подія, яка внаслідок даного випробування не може відбутися. Випадковою подією називається подія, яка може відбутися або не відбутися під час здійснення певного випробування. Вірогідною називається подія, яка внаслідок даного випробування обов’язково відбудеться ВІРОГІДНА ВИПАДКОВА НЕМОЖЛИВА

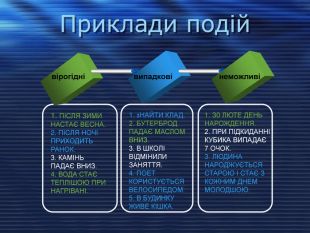
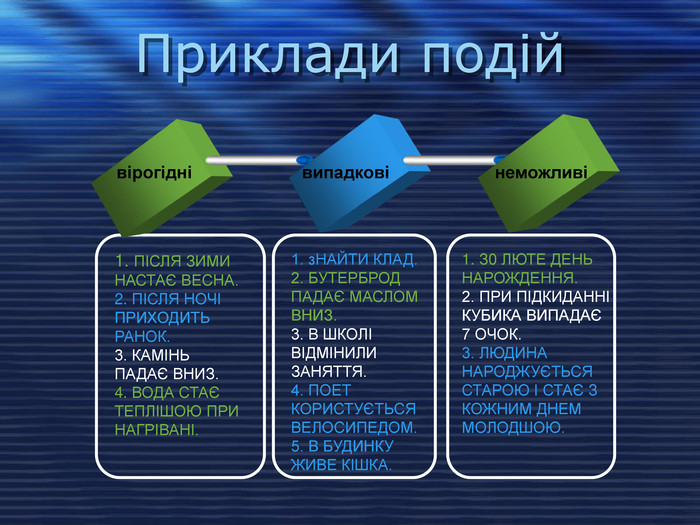
Приклади подій вірогідні випадкові неможливі 1. ПІСЛЯ ЗИМИ НАСТАЄ ВЕСНА. 2. ПІСЛЯ НОЧІ ПРИХОДИТЬ РАНОК. 3. КАМІНЬ ПАДАЄ ВНИЗ. 4. ВОДА СТАЄ ТЕПЛІШОЮ ПРИ НАГРІВАНІ. 1. зНАЙТИ КЛАД. 2. БУТЕРБРОД ПАДАЄ МАСЛОМ ВНИЗ. 3. В ШКОЛІ ВІДМІНИЛИ ЗАНЯТТЯ. 4. ПОЕТ КОРИСТУЄТЬСЯ ВЕЛОСИПЕДОМ. 5. В БУДИНКУ ЖИВЕ КІШКА. З0 ЛЮТЕ ДЕНЬ НАРОЖДЕННЯ. 2. ПРИ ПІДКИДАННІ КУБИКА ВИПАДАЄ 7 ОЧОК. 3. ЛЮДИНА НАРОДЖУЄТЬСЯ СТАРОЮ І СТАЄ З КОЖНИМ ДНЕМ МОЛОДШОЮ.

 Випадковою подією називається подія, яка може відбутися або не відбутися під час здійснення певного випробування. Наприклад: під час витягування навмання однієї карти з колоди ви взяли короля. Подія А – „взято короля ” є випадковою. Випадкові події можуть бути масовими та одиничними.

Масовими називають однорідні події, що спостерігаються за певних умов, які можуть бути відтворені (можна спостерігати) необмежену кількість разів. Наприклад, влучення або промах в серії пострілів; поява бракованих деталей при серійному випуску; радіоактивний розпад атомів речовини; і т. д. Прикладом одиничної випадкової події є падіння Тунгуського метеорита. Теорія ймовірностей вивчає лише масові випадкові величини. 

 Вірогідною називається подія, яка внаслідок даного випробування обов’язково відбудеться. Наприклад, подія А – “поява на одній із граней грального кубика натурального числа, меншого за 7” – є вірогідною. Неможливою називається така подія, яка внаслідок даного випробування не може відбутися. Наприклад, подія А – “поява на одній із граней грального кубика цифри 7” 

Виконання вправ 1. Наведіть приклади вірогідних подій. 2. Наведіть приклади неможливих подій. 3. Які із подій є вірогідними: А – „ два попадання при трьох пострілах ”; В – “навмання вибране трицифрове число не більше 1000”; С – „випадання 12 очок при киданні двох гральних кубиків”; Е – „випадання цифри 3 при киданні монети”? 4. Які із подій є неможливими: А – „випадання 13 очок при киданні двох гральних кубиків”; В – „поява слова „мама” при випадковому наборі букв а, а, м, м”. С – „чотири попадання при трьох пострілах”; Е – „поява на одній грані грального кубика числа 8”?

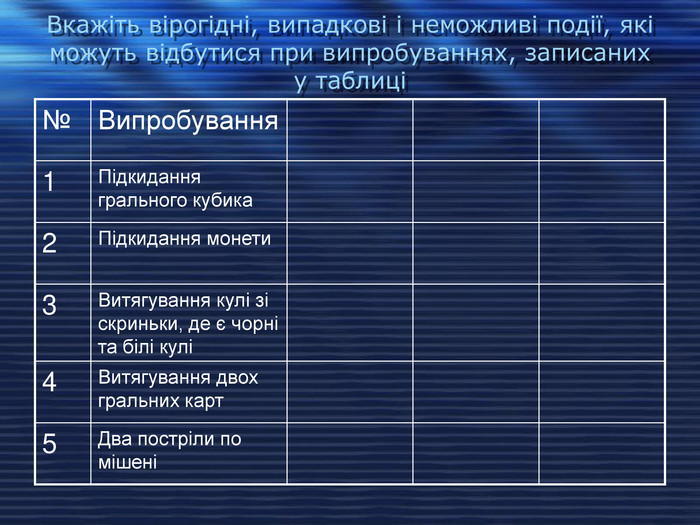
Вкажіть вірогідні, випадкові і неможливі події, які можуть відбутися при випробуваннях, записаних у таблиці № Випробування 1 Підкидання грального кубика 2 Підкидання монети 3 Витягування кулі зі скриньки, де є чорні та білі кулі 4 Витягування двох гральних карт 5 Два постріли по мішені

повна група подій попарно несумісні події рівноможливі події елементарні події.

Повною групою подій називається множина таких подій, що в результаті кожного випробування обов’язково повинна відбутися хоча б одна із них. Наприклад: у випробуванні – кидання грального кубика повну групу подій становлять події: А1 – „поява числа 1”; А2 – „поява числа 2”; А3 – „поява числа 3”; А4 – „поява числа 4”; А5 – „поява числа 5”; А6 – „поява числа 6”, Або події: В1 – „поява парного числа”; В2 – „поява непарного числа”.

Виконання вправ Чи утворюють повну групу такі групи подій: 1. Випробування – кидання монети; події: А1 – „поява герба”; А2 – „поява цифри”. 2. Випробування – кидання двох монет; події: А1 – „поява двох гербів”; А2 – „поява двох цифр”. 3. Випробування – два постріли по мішені; події: А1 – „жодного попадання”; А2 – „одне попадання”; А3 – „два попадання”. 4. Випробування – два постріли по мішені; події А1 – „хоча б одне попадання”; А2 – „хоча б один промах”. 5. Випробування – витягування карти із колоди карт; події: А1 – „поява карти червоної масті”; А2 – „поява карти бубнової масті”; А3 – „поява карти трефової масті”; А4 – „поява карти пікової масті”; А5 – „поява короля”; А6 – „поява дами”.

Попарно несумісні події – це події, дві з яких не можуть відбуватися разом. Наприклад, попадання і промах при одному пострілі – це дві несумісні події; поява цифр 1, 2, 3, 4, 5, 6 при одному киданні грального кубика – це шість несумісних подій.

Виконання вправ Чи є несумісними такі події: 1. Випробування – кидання монети; події: А1 – „поява герба”; А2 – „поява цифри”. 2. Випробування – кидання двох монет; події: В1 – „поява герба на першій монеті”; В2 – „поява цифри на другій монеті”. 3. Випробування – два постріли по мішені; події С0 – „жодного попадання”; С1 – „одне попадання”; С2 – „два попадання”; 4. Випробування – два постріли по мішені; події: D1 – „хоча б одне попадання”; D2 – „хоча б один промах”; 5. Випробування – витягування двох карт колоди; події: Е1 – „поява двох чорних карт”; Е1 – „поява туза”; Е3 – „поява дами ”;

Рівноможливі події – це такі події, кожна з яких не має ніяких переваг у появі частіше за іншу під час багаторазових випробувань, що проводяться за однакових умов. Наприклад, поява цифр 1, 2, 3, 4, 5, 6 при киданні грального кубика – рівноможливі події.

Виконання вправ Чи є рівноможливими такі події: 1. Випробування – кидання монети; події: А1 – „поява герба”; А2 – „поява цифри”. 2. Випробування – кидання неправильної (зігнутої) монети; події: В1 – „поява герба”; В2 – „поява цифри”. 3. Випробування – постріл по мішені; події С1 – „ попадання”; С2 – „промах”. 3. Випробування – кидання двох монет; події: D1 – „поява двох гербів”; D2 – „поява двох цифр”. D3 – „поява одного герба і однієї цифри”. 4. Випробування – витягування карти із колоди карт; події: Е1 – „поява карти червоної масті”; Е2 – „поява карти бубнової масті”; Е3 – „поява карти трефової масті”; Е4 – „поява карти пікової масті”; 5. Випробування – кидання грального кубика; події: F1 – „поява не менше трьох очок”; F2 – „поява не більше чотирьох очок”;

Якщо події: утворюють повну групу подій; є несумісними; є рівноможливими; то такі події називаються елементарними й утворюють простір елементарних подій.

Виконання вправ Чи утворюють простір елементарних подій такі події: Випробування – кидання монети; події: А1 – „поява герба”; А2 – „поява цифри”. Випробування – кидання двох монет; події: В1 – „поява двох гербів”; В2 – „поява двох цифр”. Випробування – кидання грального кубика; події: С1 – „поява не більше двох очок”; С2 – „поява трьох і чотирьох очок”; С3 – „поява не менше п’яти очок”; Випробування – постріл по мішені; події D1 – „ попадання”; D2 – „промах”. Випробування – два постріли по мішені; події: Е1 – „жодного попадання”; Е2 – „одне попадання”; Е3 - „ два попадання”; Випробування – витягування двох карт колоди; події: F1 – „поява двох червоних карт”; F1 – „поява двох чорних карт”;

Підведення підсумків уроку. №1. Поясніть, що таке достовірна, неможлива і випадкова подія. Наведіть приклади. №2. Вкажіть, яка з подій вірогідна, яка – неможлива і яка випадкова: а) літніх канікул не буде; б) бутерброд впаде маслом вниз; в) навчальний рік коли-небудь закінчиться. №3. Петя и Толя порівнюють свої дні народженя. Вкажіть, яка з подій вірогідна, яка – неможлива і яка випадкова: а) їх дні народження не співпадають; б) їх дні народження співпадають; в) Петя народився 29 лютого, а Толя – 30 лютого; г) дні народження обох припадають на свята – Новий рік (1 січня) і День незалежності України (24 серпня); д) дні народження в цьому році.

Домашнє завдання. Розділ 7 § 36, 37. Зап. № 1-6.