Методи розв*язування олімпіадних завдань

 Змагання в історії математики відомі з давніх давен. Ще Архімед посилав для розв’язування задачі своїм колегам і суперникам в Александрію. Математичні турніри процвітали в Неополітанському Королівстві Фрідріха ІІ Гогенштауфена (ХІІІ ст..) з яким пов’язано ім’я визначного математика європейського середньовіччя Леонардо Фібоначчі ( Леонардо Пізанський з Пізи, 1170-1250 роки).  В історії розв’язування  алгебраїчних рівнянь 3-го і 4-го порядків (ХVІ ст..) велике місце займали «Математичні змагання». Ці змагання носили особливий характер, чим сучасні олімпіади: наприклад змагання, в яких приймали участь Іоганн Палермський і Леонардо  Пізанський (ХІІІ ст.) або Ніакело Тарталья і Антоніо Фіорі (ХVІ ст..) можна називати математичними дуелями. В ХVІІІ столітті були популярні «Змагання за листуванням» в яких приймали участь Бернуллі, Лейбніц, Ньютон, Ейлер і інші. Пізніше  систематично проводились змагання на приз французької Академії наук, в яких приймали участь С.В.Ковалевська і Б.Ріман.

Математичні змагання є досить популярними серед школярів України. Це й індивідуальні змагання – математична олімпіада, командні – турнір юних математиків або математичні бої. Участь у цих змаганнях надає можливість школярам долучитися до  прекрасного світу цікавих і нестандартних задач, перевірити свої знання з математики, повірити у в власні сили або віднайти в собі хист до математики.

Історія математичного олімпіадного руху України розпочалася з Київських математичних олімпіад. Перша в Україні олімпіада пройшла в Києві в приміщенні Київського державного університету ( нині Київський національний університет імені Тараса Шевченка) у 1935 році з ініціативи видатного українського математика Михайла Пилиповича Кравчука (1892-1942). Наступного року в Київській олімпіаді взяли участь і учні інших міст України. Зокрема, у 1936 році серед переможців олімпіади був харківських десятикласник Олексій Погорєлов, який згодом пов’язав свою наукову діяльність з геометрією, ставши видатним геометром, академіком Національної академії наук України та Російської академії наук, автором шкільного підручника з геометрії, за яким кілька десятиліть успішно навчалися й радянські школярі, й українські школярі після здобуття Україною незалежності. У тому ж 1936 році було започатковано районні олімпіади та проведено першу Всеукраїнську олімпіаду.

У 1938 році М.П.Кравчука було репресовано, але небайдужі до математики молоді вчені зберегли традицію щорічно проводити Київську математичну олімпіаду. У 1942-1945 рр. під час великої Вітчизняної війни олімпіади не проводились, а потім їх проведення поновили. Важливу роль у поновленні Київської математичної олімпіади відіграв Микола Миколайович Боголюбов, що на той час був молодим професором фізико-математичного (нині механіко-математичний) факультету Київського державного університету. У післявоєнні роки до організації Київських математичних олімпіад школярів за пропозицією М.М.Боголюбова долучилися відомий  педагог та історик математики Любов Миколаївна Граціанська. На той час учні 7-10 класів, що цікавилися математикою, мали можливість щонеділі відвідувати математичні гуртки при Київському державному університеті, організацією яких керувала Л.М.Граціанська. заняття гуртка проводили студенти механіко-математичного факультету, які згодом і очолили математичний олімпіад ний рух України. Серед них А.В. Скороход, М.Й.Ядренко, В.А.Вишенський, В.І.Михайловський та інші. Гуртківці традиційно брали участь у київських математичних олімпіадах. Зазначимо, що тоді учасниками Київської олімпіади могли стати як школярі Києва, так і учні з інших міст України, бо до 1961 року олімпіада проводилася лише в Києві. І нині, за традицією, у Київській математичній олімпіаді можуть брати участь усі охочі школярі.

У 1961 році організатори Московської математичної олімпіади запросили до участі в ній школярів з різних республік тодішнього СРСР. Так відбулася перша математична олімпіада, учасники якої були з різних республік СРСР, а олімпіаду назвали всесоюзною. Участь у ній взяли й представники України. Щоб і надалі щорічно змагатися. Необхідно було відбирати сильну команду учасників, збираючи талановитих школярів по різних куточках України. Це завдання могла вирішити Республіканська математична олімпіада, у якій мали між собою змагатися переможці українських обласних олімпіад, міст Києва і Севастополя та Автономної Республіки Крим, тобто школярі з усіх регіонів України. саме 1961 рік вважають роком заснування Республіканської олімпіади – заключного етапу математичної олімпіади в Україні, який став прототипом четвертого етапу нинішньої Всеукраїнської учнівської олімпіади з математики. Отже, у 1961 році Республіканська олімпіада з математики стала освітянською подією загальнодержавного значення. Саме з її переможців надалі й формувалася команда юних математиків для участі у Всесоюзних олімпіадах.

Олімпіадні задачі в математиці – це задачі, для розв’язування яких потрібний нестандартний і оригінальний підхід. Математичні олімпіади за аналізом змісту повинні включати:

• зростання складності завдань від  першого  до наступного;
• завдання складати на основі програм з математики шкільного курсу;
• в комплект входять завдання з геометрії, алгебри, комбінаторики ( в молодших класах – по арифметиці, логічні задачі; в старших класах – по теорії чисел,   математичному аналізу); повинні бути задачі, які об’єднують різні розділи шкільного курсу.
• завдання нестандартні, які володіють певною новизною для учасників олімпіади.

Для прикладу приведу теми по яких можна складати варіанти шкільних олімпіад.

5 клас. Числові ребуси. Задачі  на розрізняння, переливання зважування. Логічні або  текстові   задачі.

6 клас. Числові ребуси. Властивості геометричних фігур. Логічні або      текстові задачі. Парність.

7 клас. Числові ребуси. Завдання на складання рівнянь. Подільність натуральних чисел. Задачі на переливання,  зважування. Логічні задачі.

8 клас. Перетворення алгебраїчних виразів. Побудова  графіків функцій. Основні елементи трикутника . Подільність натуральних чисел. Логічні задачі.

9 клас. Подільність. Квадратний  тричлен і його властивості. Перетворення алгебраїчних виразів. Основні елементи  трикутника. Задачі на комбінаторику.

Методи розв’язування олімпіадних завдань

До методів розв’язування олімпіад них завдань відносяться: Доведення від супротивного. Принцип Діріхлє. Розв’язування методами іншої науки. Правило крайнього. Розв’язування з кінця. Шукання інваріанту. Побудова контрприкладу. Математична індукція. Метод інтеграцій, аналогій, провокацій. Координатний метод. Векторний метод.

Наведу декілька методів, які широко використовуються при розв’язуванні завдань математичної олімпіади.

Метод доведення від супротивного.

Суть цього методу можна передати слідуючими пунктами:

1. Спочатку робиться припущення протилежне тому, яке потрібно довести.
2. Тоді виясняється, що випливає із даного припущення (на основі теорем, аксіом і т.п.)
3. Встановлюємо протиріччя нашого припущення із теоретичними даними.
4. Робиться висновок про те, що наше припущення є хибним, а вірне твердження протилежне тому, тобто те,   що потрібно було довести.

Принцип Діріхлє

В комбінаториці принцип Діріхлє  ( принцип ящиків) твердження, зформульоване німецьким математиком в 1834 році, яке встановлює зв’язок між об’єктами («кроликами») і контейнерами («клітками») при виконанні певних умов. В англійській або інших мовах дане твердження відомо, як «принцип голубів і ящиків».

Принцип Діріхлє застосовується в теорії діофантових наближень при аналізі системи лінійних нерівностей. Найбільш найпоширенішим формуванням цього принципу: якщо кролики розмістити в клітки, число кроликів більше числа кліток, то хоча б в одній із кліток буде знаходитись більше одного кролика.

Загальне формулювання звучить так: якщо M кроликів розмістити в N кліток, то хоча б в одній із кліток знаходитимиться не менше кроликів, а також хоча б одній клітці знаходитиметься не більше M/N кроликів.

Має право на існування і таке формулювання: якщо число кліток більше за число кроликів, то як мінімум одна клітка порожня.

Контрприклад

Контрприклад – який заперечує вірність деякого твердження. Побудова контрприкладів – звичайний спосіб заперечення гіпотези. Якщо маємо твердження « Для будь якого Х з множини М виконується властивість А» , то контрприкладом для даного твердження буде: «Існує об’єкт  із множини М,  для якого властивість А не виконується».

Щоб знайти контрприклад  трапляється певні складності. В таких випадках на допомогу приходить комп’ютер. Програма для знаходження контрприкладу може просто перебирати елементи множини М і перевіряти виконання властивості А. Більш складнішим, але ефективним є підхід в побудові контрприкладу «по частинах». При цьому вибираючи чергову «частину» відразу відкидаються варіанти, які ведуть до заперечення твердження. Це дає можливість пришвидшити роботу. Необхідно пам’ятати, що відсутність контрприкладу  не є доведенням гіпотези.

Доведення такого роду можна будувати, якщо  множина , яку ми розглядаємо, є скінченною. В цьому випадку достатньо перебрати всі елементи, і якщо контрприкладу серед них немає, то твердження буде доведене.

Інваріант

Інваріант в математиці – це властивість деякого класу (множини) математичних об’єктів залишатися незмінними при перетвореннях певного  типу.

При розв’язуванні деяких  завдань потрібно розглядати крайні випадки (правило крайнього). Більш природніше ситуація виникає тоді, коли потрібно знайти число елементів скінченної множини, а відповідь неоднозначна. При подальшому вивченні властивості елементів числової множини, бажано вивчати чи вірні умови для більшого або найменшого елемента множини (при умові, що існує найбільший і найменший елемент). Якщо мова іде про множину точок площини, то бажано розглядати крайню ліву (праву) або верхню (нижню) точки цієї площини.

Метод перебору

Метод перебору застосовується при розв’язуванні завдань в яких доводиться перебирати різні варіанти. Перебор повинен бути вірним, тобто таким, при використанні якого розглядаються всі випадки, які можуть відкинути завідомо непотрібні варіанти, що дає зменшити об’єм роботи. Застосовуються в основному тоді, коли значення шуканої величини може бути тільки цілим числом,  (а) множина значень є скінченною. Метод перебору широко застосовується при розв’язанні задач на відновлені запису при виконанні дій над числами і близьких до них  завдань на числові ребуси.

Графи

Графом на площині називають скінченну множину точок площини, деякі з них з’єднані лініями. Ці точки називають вершинами графа, а з’єднання їх лініями – ребрами. Число ребер, яка слідує із вершини графа, називають степенем цієї вершини. Прикладом графів може бути будь-яка карта  доріг, електросхема, креслення многокутників і т.п. Довгий час панувала думка, що теорія графів застосовувалась тільки при розв’язанні логічних задач.

Індукція

Індукція – метод отримання загального твердження із окремих спостережень. Метод доведення, при якому перевіряється твердження для кінцевого числа випадків, які вичерпують усі можливі варіанти називають повною індукцією. Цей метод називають методом  математичної індукції. Цей термін з’явився у 1838 році в статті де Моргана  в Британській енциклопедії. Цей метод вперше був розроблений в 1665 році Б.Паскалем. Зараз він широко використовується в математиці для доведення тотожностей, нерівностей та інших математичних тверджень. Спосіб доведення методом математичної індукції полягає в слідуючому:

1. створити базу індукції  ( доводять або безпосередньо перевіряють твердження ( формули )для n=1);
2. здійснюють індуктивний перехід (пропонують справедливість для деякого натурального числа n= k);
3. доводять справедливість твердження для n=k+1.

Заочна математична олімпіада

Основним завданням заочної математичної  олімпіади (шкільної,  об’єднаної громади, району) проявити інтерес до математики, розвивати математичні здібності учнів, створювати умови, які забезпечать можливість інтелектуально обдарованим дітям систематично на протязі навчального року приймати участь у розв’язанні математичних завдань.

Такі олімпіади можна проводити протягом навчального року в чотири тури (І, ІІ, ІІІ, IV чверті) для учнів 5-11 класів. Результати кожного туру і кінцеві (в кінці навчального року) визначають переможців кожного туру і по підсумку навчального року. Переможцям заочних олімпіад надано право приймати участь в районних олімпіадах.

В канікулярний час   проводити заняття  факультативів по розбору  розв’язків задач заочної неперервної олімпіади.

Пропоную завдання заочної неперервної математичної олімпіади для 7 класу.

Завдання 1 туру неперервної заочної математичної олімпіади

7 клас.

1. Учень не помітив знак множення між двома трьохзначними числами і написав шестизначне число, яке в сім разів більше за добуток. Знайти це число.
2. Кооператив отримує яблучний і виноградний сік в однакових бідонах і випускає яблучно-виноградний напій в однакових банках. Одного бідона яблучного соку вистачає рівно на 6 банок напою, а одного бідона виноградного – рівно на 10. Коли рецептуру напою змінили, то одного бідона яблучного соку вистачило рівно на 5 банок напою. На скільки банок напою вистачає    одного бідона виноградного соку? (напій водою не розбавляється)
3. У вершинах трикутника записано по одному натуральному числу, на кожній стороні – добуток чисел, які написані на кінцях сторін, а в середині трикутника – добуток чисел записаних у його вершинах. Сума всіх чисел рівна 1000. Які числа записані у вершинах трикутника?
4. Дерев’яний куб пофарбували з усіх сторін, а згодом розпилали його на 27 однакових кубиків. Скільки серед кубиків мають одну, дві, три зафарбованих грані ?. Скільки кубиків  не пофарбовані?
5. Довести, що 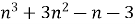   ділиться на 48 при довільних непарних n.

Завдання 2 туру.

1. Дано три різні не рівні нулю цифри. Із них складаються всі можливі тризначні числа. Довести, що сума цих чисел обов’язково ділиться на 6 і 37.
2. Клітинки шахматної дошки заповнюються числами  таким чином, що сума будь яких чотирьох  чисел, які стоять у клітках розташованих «буквою Г» (хід шахматного коня), одна і та ж сама. Скільки чисел використано при такому заповненні?
3. Знайти всі цілі значення n, при яких 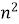+2n+6 ділиться на n+4.
4. Нехай  (а ) непарне натуральне число, а (в) – натуральне число. Довести, що числа а та ав+4 – взаємно прості.
5. У футбольному  турнірі, в якому кожна із 8 команд зіграла з кожною  по одному разу, набрали слідуючі число очок: 14, 12, 8, 8, 6, 4, 3, 1. Яку кількість очок команди, що зайняли перші чотири місця  втратили в іграх з рештою команд? (за перемогу дається 2 очки, нічия – 1 очко, поразка – 0 очок)

Завдання 3 туру.

1. 101 кінь розмістили в 15 конюшнях. Чому хоча би в одній конюшні буде обов’язково непарне число коней?
2. Ділене зменшили на 10%, а дільник збільшили на 10%. Як зміниться частка?.
3. В деякий момент часу Венера і Меркурій займають певне положення  відносно зірок. Через скільки  діб обидві планети будуть знову знаходитись в тому ж положенні відносно зірок,  якщо відомо, що Меркурій робить повний оберт навколо Сонця за 88 діб, а Венера за 225 діб?.
4. На конгрес приїхала велика кількість учених, один з них був раніше  знайомий один з одним, а інші - ні. При цьому два з учених, що мають одне і теж саме число знайомих, не мають спільних знайомих. Довести, що серед присутніх на конгресі учених знайдеться вчений,  знайомий рівно з одним учасником конгресу.
5. Чи можна розрізати круг на декілька частин, з яких скласти квадрат?

Завдання 4 туру.

1. У змаганнях приймає 6 футбольних команд. Відносно учасників фінальної гри були висловлені деякі припущення:

1. команда a і с;
2. команда в і с;
3. команда  g і а;
4. команда  в і g;
5. команда а і d.

Відомо, що в одному із припущень дві команди були названі невірно, а в інших була названа вірно тільки одна команда. Які команди приймали участь у фіналі?

2. 6 карасів важчі 10 лящів, але легші 5 окунів; 10 карасів тяжчі 8 окунів. Що важче: 2 карася чи 3 ляща?
3. Розташуйте цифри від 1 до 8 по вершинах куба таким чином, щоб сума чисел, які стоять у вершинах кожної грані були рівні.
4. Коли пасажир проїхав половину шляху, він став дивитись у вікно і дивився до тієї миті поки не залишилося проїхати половину того шляху, що він проїхав дивлячись у вікно. Яку частину всього шляху пасажир дивився у вікно?
5. Сума двох чисел більша за їх добуток, але менша їх різниці. Встановити, додатні чи від’ємні ці числа.

Неперервна заочна олімпіада проводилася на протязі двох років. Інтелектуально обдаровані діти були виявлені і педагоги високо оцінили значимість цього виду діяльності. Було відмічено підвищення активності інтелектуально обдарованих дітей, збільшився інтерес учнів до розв’язування олімпіадних завдань. Значимий успіх переможців шкільної неперервної заочної олімпіади у 2-му турі районної олімпіади.