Особливості методики розв'язування задач в 5-6 класах
Особливості методики розв’язування задач 5-6 класах
Зміст
ВСТУП………………………………………………………………………….3
Розділ І. Суть, класифікація та способи розв’язування …………………….8
- Поняття текстової задачі……………………………………………….8
- Класифікація текстових задач…………………………………………11
- Способи і методи розв’язування задач………………………………..13
Висновки до першого розділу…………………………………………….17
Розділ ІІ. Методичні прийоми розв’язування задач різних типів…………30
- Задачі на рух……………………………………………………………31
- Задачі на змішування…………………………………………………..35
- Диференційоване навчання розв’язуванню задач…………………..42
- Текстові задачі в закордонних школах………………………………47
Висновки до другого розділу…………………………………………….52
Розділ ІІІ. Дослідження практики роботи учнів і вчителів щодо розв’язування текстових задач……………………………………………………………….53
- Дослідження умінь учнів розв’язувати текстові задачі…………….53
- Типові методичні помилки вчителів…………………………………57
- Методичні рекомендації вчителям, щодо навчання учнів розв’язувати текстові задачі………………………………………………………..65
Висновки до третього розділу…………………………………………..68
Розділ ІV. Горіння, його види. Умови, необхідні для горіння. Різновидності горіння……………………………………………………………………….69
Висновки до четвертого розділу………………………………………..76
Загальні висновки……………………………………………………………77
Список використаних джерел………………………………………………79
Додатки……………………………………………………………………….87
ВСТУП
Провідною тенденцією розбудови освітньої системи в Україні взагалі і шкільної зокрема є зумовлений змінами тенденцій розвитку суспільства перехід до нової парадигми освіти. Діяльність освітян у XX столітті здебільшого була орієнтована на формування стабільної системи знань, навичок і вмінь, а тому освіта мала репродуктивну модель. У сучасному інформаційному суспільстві період „життя нових знань» скоротився до 3-5 років. Тому лише їх отримання в традиційному розумінні вже не може бути метою навчання. Для підготовки до життя підростаючого покоління стає нагальною потреба у сформованості здібностей до самовизначення та саморозвитку кожного члена суспільства, його неперервної освіти. Сучасній школі потрібно одночасно з розвитком інтелекту і творчих здібностей формувати в усіх дітей готовність до дій в умовах майбутнього, основні тенденції якого можуть бути зовсім не пов’язані з сьогоденням.
Математична освіта є важливою складовою загальноосвітньої підготовки школярів. Місце математики в системі шкільної освіти визначається її роллю в інтелектуальному, соціальному і моральному розвитку особистості, розумінні будови і використанні сучасної техніки, розвитку економіки, інформаційно-комунікаційних технологій, сприймання наукової картини світу і сучасного світогляду. Математика є опорним предметом при вивченні суміжних дисциплін, тому без належної математичної підготовки неможлива повноцінна освіта сучасної людини. Вирішальне значення для системи шкільної освіти має формуючий вплив предмета математики на особистість школяра. Ідеться, насамперед, про розвиток мислення і логічного мислення зокрема, просторових уявлень і уяви, алгоритмічної та інформаційної культури, творчості, уваги, пам’яті, позитивних якостей особистості та рис характеру, емоційно-вольової сфери.
Традиційно розв’язування різного виду задач вважалось і предметом навчання математики, і ефективним засобом формування математичних знань і вмінь, інтелектуального розвитку і виховання учнів. Розв'язування текстових (сюжетних) задач займало значне місце в традиційному курсі шкільної арифметики. І це не випадково. Ці задачі добре розвивають мислення, кмітливість, винахідливість учнів, готують їх до формування вмінь розв'язувати задачі методом рівнянь, сприяють підсиленню прикладної спрямованості навчання математики.
Проте з 60-х років минулого століття у зв’язку з реформуванням шкільної математичної освіти доля використання текстових задач в основній школі почала суттєво зменшуватися.
Зазначені обставини негативно вплинули на рівень математичної освіти і розумового розвитку учнів. Погіршився і стан навчання учнів розв’язуванню текстових задач за допомогою методу рівнянь, про що свідчать наслідки вступних іспитів до вищих навчальних закладів.
Сьогодні у зв’язку з реформуванням системи освіти в Україні, Росії та інших країнах СНД знову посилився інтерес до тих компонентів змісту шкільного курсу математики, які сприяють розвитку мислення і творчої особистості учнів. До таких компонентів належать і текстові задачі. У зв’язку з цим постало питання про відновлення їх місця і ролі у програмі та підручниках з математики основної школи.
Автори концепції математичної освіти 12-річної школи, формулюючи пріоритети розвитку і принципи відбору змісту, зазначили, що математичне моделювання є важливим засобом для розкриття гносеологічного значення математики. Це означає, що зміст навчального матеріалу мас бути таким, щоб кожен учень міг засвоїти всі три етапи застосування математики до розв’язування задач, що виникають у людській практиці: 1) формалізація (перехід від ситуації, описаної в задачі, до формальної математичної моделі); 2) розвязування задач у межах побудованої моделі; 3) інтерпретація одержаного розв’язання задачі та застосування його до вихідної ситуації. Основним засобом для ознайомлення учнів із моделюванням є розв’язування сюжетних задач, які в свою чергу є текстовими моделями проблемних ситуацій, що можуть зустрітися в людській практичній чи професійній діяльності.
Тому у сучасній школі до традиційних цілей використання текстових задач як основної форми закріплення теоретичних знань та їх застосування на практиці, як засобу для розвитку мислення та кмітливості, підтримання постійного інтересу до математики (як до навчального предмета так і до самого процесу навчання), як допоміжного чинника в здійсненні різних аспектів виховання та професійної орієнтації учнів приєднується мета з формування за їх допомогою вмінь математизувати ситуації під час дослідження різних явищ природи і суспільства.
У процесі навчання математичні задачі відіграють значну роль. Вони сприяють кращому осмисленню теоретичного матеріалу, його запам’ятовуванню, дають можливість пов’язувати викладання математики з життям та іншими науками, виховують активність, самостійність, наполегливість та інші позитивні риси. Психологи Г.П.Бевз, І.М.Богданович, Б.М Колесніков, Д.Ю. Пойа, П.В.Стратілов та ін. відзначають, що задачі діють на людський мозок різносторонньо, оскільки виконують пізнавальну, дидактичну, розвивальну та прикладну функції. Математичні задачі впливають на активізацію мислення, уваги, пам’яті школярів, стимулюють їх творчу думку. Саме із задач починається зацікавленість багатьох учнів математикою. Ось чому на уроках математики приблизно половину всього часу використовують для розв’язування різних задач .
Розв’язування математичних задач являє собою найближчу до характеру щоденного мислення математичну діяльність. Д.Пойа підкреслює в своїх працях, що ми зустрічаємось у задачею кожен раз, коли шукаємо засоби для досягнення мети. Так само, як щоденні задачі є центром нашого життєвого ситуативного мислення, також можна досягти того, щоб математичні задачі стали центром вивчення математики. Свої теоретичні та методичні дослідження цій темі присвятили Г.П.Бевз, І.М.Богданович, Б.М Колесніков., Д.Ю.Пойа, П.В.Стратілов та ін.
Задачам приділено багато уваги у методичній літературі, причому найбільше розроблено і досліджено методику розв’язування задач арифметичних і геометричних. Важливе місце займає питання класифікацій, які б допомагали визначати систему розв’язування задач відповідно до їх типів. Вивченням і складанням класифікації задач займалося чимало вчених, погляди яких не співпадали (М.В. Богданович, І.В. Бетюкова, М.О. Бантова, А.А. Столяр, М.Н. Нікітін). Тому в сучасній методичній літературі немає єдиного підходу до вирішення цієї проблеми. Спільною рисою всіх класифікацій, на нашу думку, є те, що всі дослідники за основу брали виявлення співвідношення та залежностей між величинами, розкриття конкретного змісту арифметичних дій та їх кількість.
Активізація творчої самостійності учнів, формування їх мислення в процесі оволодіння математикою найефективніше здійснюється через розв’язування задач. Зокрема, важливість текстових задач обумовлюється особливостями наукової структури курсу математики 5-9 класів.
Робота учнів з сюжетними текстовими задачами, особливо з тими, формулювання яких спирається на життєвий досвід учнів, допомагає підтримувати постійний інтерес до процесу навчання, розвивати кмітливість та інтуїцію, сприяє розширенню кругозору, економічному вихованню та професійної орієнтації учнів.
Важливо навчити учнів розв’язувати текстові задачі в усіх класах, бо від цього значною мірою залежить не тільки навчання учнів математики на даному етапі, а й результативність їх наступної навчальної і трудової діяльності.
Проблема розвитку логічного мислення учнів при навчанні математики пов’язана зокрема, з формуванням прийомів мислення в процесі навчальної діяльності. Ці прийоми мислення ( аналіз, синтез, абстрагування тощо) особливо яскраво проявляються під час розв’язуванні задач, зокрема текстових (сюжетних). Але ефективність формування цих прийомів значною мірою залежить від того, як організовано пізнавальну діяльність учнів.
Отже, текстові задачі - одна з найбільш важливих складових шкільного курсу математики. Розв’язування цих задач відіграє важливу роль в загальному розвитку учнів, у розвитку їх зацікавленості математикою.
Зрозуміло, що намагання класифікувати текстові задачі спрямовані на уніфікацію шляхів пошуку способів розв’язування задач,але, на жаль, деякі задачі можуть передбачати різні способи розв’язування, тому не можуть бути точно класифіковані. Важливість впливу розв’язування задач на мислення учнів і їхній загальний розвиток, а також недостатнє вирішення цієї проблеми в методичній літературі зумовили вибір теми дослідження.
Об’єкт дослідження - методика навчання математики, предмет - способи розв’язування різних типів текстових задач і методика пояснення цього процесу учням основної школи.
Мета дослідження - визначити основні принципи, покладені в основу класифікацій задач, і розробити методичні прийоми для їх розв'язування.
Гіпотеза: спосіб розв’язування задачі залежить від класу задач, до яких вона належить, тому уміння розв’язувати текстові задачі залежить від уміння їх класифікувати.
Відповідно до мети і гіпотези було сформульовано завдання дослідження:
- Визначити такі основні поняття як текстова задача, складена задача, проста задача, здійснити класифікацію задач.
- Представити основні способи розв’язування різних типів текстових задач.
- Дослідити стан готовності учнів розв’язувати задачі, визначити типові помилки учнів і вчителів.
- Розробити методичні прийоми розв’язування задач, запропонувати методичні рекомендації щодо навчання учнів розв’язуванню задач.
Методи, що використовувались у процесі дослідження
- теоретичні: вивчення наукової літератури, аналіз класифікації текстових задач, аналіз методів розв’язування;
- емпіричні: опитування учнів, бесіди з учителями, тестування, анкетування, оцінювання учнівських робіт
Експерементальною базою дослідження були учні 5-9 класів загальноосвітньої школи І-ІІІ ступенів смт. Наркевичі. У процесі дослідження враховувся досвід учителів математики шкіл Наркевицької ОТГ.
Апробація результатів дослідження здійснювалася в період з грудня 2018 по травень 2019 року включно. Основні положення роботи на різних етапах експерименту обговорювалися на науково-практичних конференціях.
РОЗДІЛ 1
СУТЬ, КЛАСИФІКАЦІЯ ТА СПОСОБИ РОЗВЯЗУВАННЯ ЗАДАЧ
1. Поняття текстової задачі
Слово “задача” мас багато різних значень. Тому дати досить чітке означення цьому поняттю неможливо. Проте можна коротко описати його зміст.
Математика виникла із задач. Розв’язання було головною складністю в навчанні математиці з часів папіруса Ринда: найдавніші єгипетські математичні папіруси не містять ше ніяких доведень, означень чи аксіом, а являють собою збірки задач, здебільшого геометричних, правил і формул для обчислення площ і об’ємів. Те саме можна сказати і про математику Вавилону та інших країн стародавнього Сходу. Працю Евкліда можна розглядати як педагогічне досягнення, адже вона розкриває геометрію в зрозумілих задачах. Російські математичні рукописи 17-18 століть теж містять в основному задачі і їх розв’язання.
В “Арифметиці” Магницького до задач додавалися розв’язки, які необхідно було „ввытверживать”. Способи розв’язування задач подавалися у вигляді багатослівних правил, і ці правила учні повинні були завчати. Зміст задач охоплював усі типові життєві ситуації, які вимагали відповідних практичних розрахунків: купівлю-продаж, витрати і накопичення. Задача була метою навчання, тобто математику, власне, вчили для того, щоб засвоїти правила розв'язування аналогічних задач.[67]
Певна група задач з найбільш яскравими методами розв’язування починає потім переходити з підручника в підручник, доповнюючись серіями аналогічних, задачі стають типовими. Незважаючи на те, що деякі з них втратили свій практичний зміст, невміння їх розв’язувати розцінювалося як арифметична неграмотність. Здібність привести задачі до визначеного типу вважалася показником високо розвинутого мислення.
Нa сучасному етапі задачі поступово набирають ілюстративного значення: вони використовуються для більш ефективного засвоєння теоретичних відомостей, обсяг яких значно збільшився. Цю думку зустрічаємо в працях С.І. Шохор-Троцького: «Арифметичні задачі взагалі повинні, при розумному навчанні, бути не метою, а тільки засобом навчання арифметики».
Отже, задачі стимулювали не тільки виникнення математичної науки, а й її розвиток.
Насамперед задачі, створені життям, змушували вчених розробляти нові алгоритми, розкривати закономірності відношень у величинах, створювати нові методи дослідження, - тобто збагачувати математику новими відкриттями. Так, наприклад, задачі про азартні ігри привели Б.Паскаля та П.Ферма до теорії ймовірностей, без якої сучасний світ майже не уявляс свого існування; дослідження задачі про оптимальне завантаження верстатів Л. Канторовичем привело до створення лінійного програмування, і це лише мала доля всіх відкриттів.
Існують різноманітні задачі і всякого роду відмінності між задачами. Однак найбільш важливою є відмінність між стандартними і нестандартними задачами. Задача, яка не розв’язується за відомим стандартом, вимагає творчого підходу, що позитивно впливає на розумовий розвиток.
Рузін Н.К. вказує на те, що стандартні задачі - це задачі, які вимагають використання добре відомого правила, тому являють собою те ж саме, що і просте питання словника. Багато вчених вважають, що від такої задачі можна досягти лише «маленької ізольованої ланки механічного пізнання», хоча цей тип задач в необхідній дозі є корисним. [33]
Історично відомо, що математичні знання передавалися із покоління в покоління у вигляді списку задач та їх розв’язування. В стародавні часи навченим вважався той, хто вмів розв’язувати задачі певних типів, що зустрічалися на практиці (наприклад, у торгівлі). При цьому усвідомленню використання того чи іншого способу дій достатньо уваги не приділялося.
Проте згодом текстові задачі знайшли своє застосування. Оскільки, основна лінія арифметики - лінія числа - ще не була розроблена, тому навчання обчисленням проводилося через задачі. Наприклад, дріб розглядався не просто ![]() (одна четверта), а
(одна четверта), а ![]() яблука (одна четверта яблука). Сучасна школа також цим користується. В підручниках з математики для 5 класу доведення нерівності
яблука (одна четверта яблука). Сучасна школа також цим користується. В підручниках з математики для 5 класу доведення нерівності ![]() проводиться на прикладі двох яблук, кожне з яких розрізають на три рівні частини. Згодом, за допомогою задач, формувалися важливі навчальні вміння, а саме: аналіз тексту, виділення умови задачі та головного питання, складання плану розв'язування, пошук умов з яких можна отримати відповідь та перевірки отриманих результатів. [27,63]
проводиться на прикладі двох яблук, кожне з яких розрізають на три рівні частини. Згодом, за допомогою задач, формувалися важливі навчальні вміння, а саме: аналіз тексту, виділення умови задачі та головного питання, складання плану розв'язування, пошук умов з яких можна отримати відповідь та перевірки отриманих результатів. [27,63]
Важливу роль відігравало також привчання учнів до перекладу тексту на математичну мову: мову арифметичних дій, рівнянь, нерівностей, графічних образів. Використання арифметичного способу розв’язування задач сприяло загальному розвитку учнів, формуванню не тільки логічного, а й образного мислення, кращому засвоєнню математичної мови, а це, в свою чергу, підвищувало ефективність навчання математики і суміжних їй дисциплін.
Актуальними в роботі вчителів математики залишаються питання співвідношення арифметичних і алгебраїчних способів розв’язування текстових задач, пропедевтичної роботи, формування навичок, що є важливим для успішного оволодіння методом рівнянь тощо.
У шкільному курсі математики існують задачі, в яких дані і зв'язок між ними включені у певну фабулу. Зміст цієї фабули є сюжетом, де відображено ситуацію, близьку до життєвої, практичної. У ній описується кількісний аспект реального явища чи події і міститься вимога знайти невідоме значення деякої величини або величин. Такі задачі називаються сюжетними. Оскільки ці задачі сформульовано природною (нематематичною) мовою, то часто їх називають також текстовими. [48]
Зміст поняття текстової задачі може бути ширшим, оскільки фабула їх може бути пов’язана і з абстрактними подіями. В методичній літературі зустрічається також і назва задачі на складання рівнянь. Остання є досить умовною, оскільки розв’язувати ці задачі можна різними способами:
- алгебраїчним, при якому складається рівняння;
- арифметичним, за яким усі логічні операції при розв’язуванні задач проводяться над конкретними числами, і основою міркування є знання змісту арифметичних дій;
- комбінованим, який поєднує як арифметичний, так і алгебраїчний способи розв’язування;
- логічними міркуваннями.
Грамотно організований процес розв’язування текстових задач стимулює розвиток логічного мислення учнів, формує їхню розумову культуру.
Термін “задача” вживається в різних значеннях. У найширшому плані можна сказати, що задача передбачає необхідність свідомого пошуку відповідних засобів для досягнення мети, яку добре видно, але яка безпосередньо недосяжна. У психологічному аспекті задача розглядається як свідома мета, що існує в певних умовах, а дії - як процеси або акти, спрямовані на досягнення її, тобто на розв’язування задачі. [4]
Важливим при навчанні розв'язувати сюжетні задачі є засвоєння учнями певних рекомендацій, яких варто дотримуватися, розв'язуючи певні типи задач, наприклад на рух, сумісну роботу, сплави і суміші тощо.
2. Класифікація текстових задач
Задачі, які розв'язуються в школі, розрізняються в першу чергу характером своїх об'єктів. В одних задачах об’єктами є реальні предмети, в інших — всі об'єкти математичні.
![]() практичні(реальні)
практичні(реальні)
![]() По характеру об’єктів
По характеру об’єктів
математичні
Практичною задачею ми називаємо задачу, в якій хоча б один об’єкт є реальним предметом.
Під математичною задачею розуміють будь яку вимогу обчислити, побудувати, довести що-небудь, що стосується кількісних відношень і просторових форм, створених людським розумом на матеріалістичній основі знань про навколишній світ. [69]
Розв’язати математичну задачу - це значить знайти таку послідовність спільних положень математики (визначень, аксіом, теорем, правил, законів, формул), застосовуючи які до умов задачі або до їх наслідків, отримаємо те, що вимагається в задачі, - її відповідь.
![]() стандартні
стандартні
![]() По відношенню до теорії
По відношенню до теорії
нестандартні
Стандартна задача складається з послідовності кроків, кожен із яких є умовою задачі або буде знайдений в процесі слідування. Тому пошук цієї послідовності кроків - це найголовніше, що потрібно робити для того, щоб розв’язати стандартну задачу.
Математика і займається тим, що встановлює для багатьох видів задач правила, користуючись якими можна знайти вказану послідовність кроків для розв’язування будь-якої задачі даного виду.
Для багатьох видів задач такі правила вже давно знайдені. Правила, користуючись якими можна знайти послідовність кроків для розв’язування для будь-якої задачі деякого виду, в математиці викладається в різних формах.
В означенні стандартних задач, яке було дане в якості основної ознаки цих задач вказано наявність таких спільних правил або положень, які однозначно визначають програму розв’язування цих задач і виконання кожного кроку цієї програми. Звідси зрозуміло, що нестандартні задачі - це такі, для яких немає спільних правил і положень, які визначають точну програму їх розв’язування.[ 1,66]
3.Способи і методи розв’язування задач
Спосіб розв’язування задачі прямо залежить від її типу, в першу чергу від того, проста вона чи складена.
Розв’язування складеної задачі полягає в тому, що її розкладають па ряд простих задач (подають план розв’язування). Воно може бути виконано, як було згадано раніше, двома способами: синтетичним і аналітичним.
Синтетичний спосіб розв’язування складеної задачі полягає в тому, що виходячи з числових даних задачі, складається і розв’язується перша проста задача, потім складається друга проста задача з числових даних (в ряді випадків використовуючи число, знайдене при розв’язувані першої простої задачі) і так продовжується доти, поки відповідь на останню просту задачу не буде відповіддю на запитання складеної задачі.
Аналітичний спосіб полягає в тому, що розбір (аналіз) задачі починається із загального запитання задачі. Потім поступово, поділяючи задачі на частини, доходять до питання, для розв’язування якого є дані. І, нарешті, складають план розв’язування задачі [28,56].
Пояснимо застосування вказаних способів розв’язування арифметичних задач на прикладі:
Із котловану потрібно вивезти 1200 т землі. Вивозять 5 семитонних і 4 п'ятитонних самоскидів. Кожна машина зробила 15 рейсів. Скільки залишилося невивезеної землі?
Аналітичний спосіб розв’язування задачі
- Скільки тонн землі залишилося в котловані після того, як кожен самоскид зробив 15 рейсів?
- Скільки тонн землі вивезли 4 п’ятитонні самоскиди за 15 рейсів?
- Скільки тонн землі вивезли 4 п’ятитонні самоскиди за один рейс?
- Скільки тонн землі вивезли 5 семитонних самоскиди за 15 рейсів?
- Скільки тонн землі вивезли 5 семитонних самоскиди за один рейс'?
Синтетичний спосіб розв’язування задачі
- Скільки тонн землі вивезли 5 семитонних самоскиди за один рейс?
- Скільки тонн землі вивезли 5 семитонних самоскиди за 15 рейсів?
- Скільки тонн землі вивезли 4 п'ятитонні самоскиди за один рейс?
- Скільки тонн землі вивезли 4 п’ятитонні самоскиди за 15 рейсів?
- Скільки тонн землі вивезено всіма самоскидами за 15 рейсів?
- Скільки тонн землі залишилося невивезеної з котловану після того, як кожен самоскид зробив 15 рейсів? [29]
На практиці у більшості випадків аналіз і синтез при розв’язуванні складених арифметичних задач взаємно переплітаються і доповнюють один одного.
Задачі можна розв’язувати такими способами: складанням загальної числової формули і з попереднім стислим аналізом; за запитаннями з наступним обчисленням після кожного запису; за запитанням з повним формулюванням відповідних простих задач; з попереднім складанням плану і наступним обчисленням; з поясненням у стверджувальній формі (пояснення подають перед дією або після дій); виконанням дій без формулювання запитань з наступним зв’язним поясненням; з поясненням, яке дається разом з виконанням дій; з поясненням, у якому виділено окремі етапи розв’язування; з поясненням кожної дії у формі запитань та їх обгрунтувань. [11]
Існують різні форми письмового розв’язання арифметичних задач, які відрізняються головним чином характером елементів пояснення, їх місцем і обсягом.
Для прикладу наведемо деякі форми розв’язання такої задачі:
Відношення добового видобутку вугілля першої і другої шахт ![]() . Добовий видобуток третьої шахти становить 54% добового видобутку вугілля першої і другої шахт разом узятих. Скільки видобули вугілля за добу всі три шахти разом, якщо третя шахта видобувала на 1225 т більше, ніж друга?
. Добовий видобуток третьої шахти становить 54% добового видобутку вугілля першої і другої шахт разом узятих. Скільки видобули вугілля за добу всі три шахти разом, якщо третя шахта видобувала на 1225 т більше, ніж друга?
Розглянемо типові способи розв’язування задач арифметичним методом.
І. За запитаннями з наступним обчисленням після кожного запитання.
Замінюємо відношення дробових чисел відношенням цілих чисел, наприклад, ![]()
- Скільки частин становить добовий видобуток вугілля першої і другої шахт разом?
- + 2 = 5 (частин)
- Скільки частин становить добовий видобуток вугілля третьої шахти?
5 * 0,54 = 2,7 (частини)
Відношення добових видобутків вугілля трьох шахт замінюємо відношенням цілих чисел:
3 : 2 : 2,7 = 30 : 20 : 27
- Скільки частин становить 1225 т вугілля?
27 - 20 = 7 (частин)
- Скільки тонн вугілля припадає на одну частину?
1225 : 7 = 175(т)
- Скільки частин становить добовий видобуток вугілля трьох шахт?
- + 2 + 2,7 =7,7 (частин)
ІІ. Розв’язування задач з поясненнями в стверджувальній формі
• Пояснення подаються після дій.
![]() - відношення добових видобутків вугілля першої і другої шахт записано у вигляді відношення цілих чисел.
- відношення добових видобутків вугілля першої і другої шахт записано у вигляді відношення цілих чисел.
- 3 + 2 = 5 (частин) становить добовий видобуток вугілля першої і другої шахт разом.
- 5*0,54 = 2,7 (частин) становить добовий видобуток вугілля третьої
шахти.
- 3 : 2 : 2,7 = 30 : 20 : 27— відношення добових видобутків вугілля трьох шахт записано у вигляді відношення цілих чисел.
- 27 - 20 = 7 (частин) - становить 1225 т вугілля.
- 1225 : 7 = 175 (т) вугілля припадає на одну частину.
- 30 + 20 + 27 = 77 (частин) становить добовий видобуток вугілля трьох шахт.
- 175 * 77 = 13475 (т) - видобули вугілля за добу три шахти разом.
Пояснення подаються перед розв’язком задачі.
-
Якщо добовий видобуток першої шахти становить 3 частини, а другої - 2 частини (
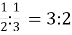 ), то добовий видобуток першої і другої шахт становить: 3+2 = 5 (частин)
), то добовий видобуток першої і другої шахт становить: 3+2 = 5 (частин)
- Добовий видобуток вугілля третьої шахти становить:
5*0,54 = 2,7 (частини)
Після заміни відношення дробових чисел відношенням цілих чисел дістанемо відношення добових видобутків вугілля трьох шахт у вигляді відношення цілих чисел.
З : 2 : 2,7 = 30 : 20 : 27
- 1225 т вугілля становлять: 27 - 20 = 7 (частин).
- На одну частину припадає: 1225 : 7 = 175 (т вугілля).
- Добовий видобуток вугілля трьох шахт становить: 30 +20+ 27 = 77 (частин).
- Три шахти разом за добу видобули вугілля:
175 - 77= 13475 (т).
4.Розв’язування задач за допомогою рівнянь
Згідно з діючою програмою з математики, розв’язування текстових задач за допомогою рівнянь передбачено вже в першій темі 5 класу. Проте, в 5-6 класах захоплюватися алгебраїчним методом розв’язування таких задач не варто. Пов’язано це з віковими особливостями розвитку мислення учнів. Уміння абстрактно мислити в більшості учнів цієї вікової групи ще не сформоване, а тому, в них переважає конкретно-понятійне мислення над абстрактно- понятійним. Більшого розвитку досягла практична компонента мислення порівняно зі словесно-логічною. Крім того, у п’ятикласників і шестикласників ще не сформовані навички, необхідні для кісного опанування алгебраїчного методу розв'язування задач. А саме: вираження невідомих величин через відомі, бачення двох однакових величин, виражених по різному, виконання тотожних перетворень виразів зі змінною. [53]
Взагалі, метод рівнянь ефективно застосовувати при розв’язуванні таких задач, де невідоме в рівнянні фігурує хоча б у двох місцях, наприклад:
![]() і т.п.
і т.п.
Однак, такі рівняння важко розв’язати, спираючись на залежність між компонентами і результатом арифметичних дій.
Отже, розв’язувати задачі складанням рівняння в 5 класі варто лише в окремих випадках, як демонстрацію ще одного способу розв’язування текстової задачі і відповідну пропедевтику алгебраїчного методу.
З огляду на вищесказане, в 5-6 класах має переважати арифметичний спосіб розв’язування задач, а вже з 7 класу - метод рівнянь. Зрозуміло, що в сучасній школі не варто повертатися до застарілих способів розв’язування арифметичних задач, досить обмежитися двома-трьома типами:
- на пропорційний поділ;
- на знаходження чисел за їх сумою та різницею;
- на знаходження чисел за їх сумою (різницею) та кратним відношенням.
[50]
У 5-6 класах варто цілеспрямовано формувати навички, що є важливими для успішного оволодіння алгебраїчним методом розв’язування текстових задач, а саме: записувати у вигляді виразу словесно сформульовані залежності та складати рівності.
Формуванню навички записувати у вигляді виразу словесно сформульовані залежності сприятимуть вправи такого типу:
- У класі х хлопчиків, а дівчаток на 4 більше. Скільки дівчаток у класі? Запиши це у вигляді буквеного виразу.
- У парку х дубів, а берізок у 3 рази більше. Скільки берізок у парку? Склади вираз для розв’язування задачі.
- Пшеницею засіяно х га, а житом - 40% цієї площі, тобто житом засіяно .... га.
- Сума двох чисел дорівнює 17. Одне з цих чисел х. Запишіть буквеним виразом друге число.
- В одному ящику а кг груш, а в другому - на 4 кг менше. Яка маса груш в обох ящиках?
- Власна швидкість човна – х км/год, швидкість течії річки 2 км/год. З якою швидкістю човен рухається за течією? Яку відстань при цьому він долає за 4 год? [15]
Формувати навички складати рівності варто за етапами:
На першому етапі необхідно навчити учнів розуміти зміст уже складених рівностей. Цьому можуть сприяти такі вправи: сформулювати словами як співвідносяться числа а і с:
- а = с + 2
Міркування повинні бути такими: - а на 2 більше від с,
- с на 2 менше від а,
- різниця чисел а і с дорівнює 2
- а = 3*с;
- а = с*2
-
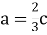
- а - с = 4
-
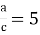 і т.д.
і т.д.
На другому етапі учні мають самі складати відповідні рівності, де співвідношення між числами, що порівнюються, мають бути подані у явному вигляді. Наприклад: записати за допомогою рівності такі співвідношення між числами х та у:
- х на 3 менше у
Міркування мають бути такими: щоб з даних чисел утворювати рівні між собою числа, можна:
- менше число х збільшити на 3, тобто записати у=х+3;
- більше число у зменшити на 3, тобто записати х = у-3;
- третій варіант запису може бути таким: у-х = 3 .
- Число х більше від числа у в 3 рази
Також маємо три варіанти рівностей:
- х = 3у;
-

-
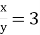
- у становить 25% від х
- різниця чисел х і у в 2 рази менша за суму цих самих чисел
- у на 15% менше х і т.д.
Третій етап. Учні виконують вправи на використання відомих формул, записують неявно подані рівності. Наприклад: периметр квадрата рівний (х + 12) см, а довжина його сторони - х см. Скласти рівняння периметра квадрата та визначити довжину сторони квадрата. [14]
Розв’язування сюжетної задачі має починатися з усвідомлення її змісту. Для цього, як правило, учням недостатньо прочитати умову задачі або навіть її переказати. Зміст задачі необхідно усвідомити та осмислити, а для цього проаналізувати. Якщо учні розв’язують задачу самостійно, то їм доцільно дати такі рекомендації, щодо засвоєння змісту.
- Прочитайте не менше ніж два рази текст задачі, так, щоб могли його повторити;
- Визначте величини, про які йдеться в умові задачі;
- Розмежуйте в умові задачі дані і шукані величини;
- Встановіть залежність між даними і шуканими величинами;
- Визначте головне запитання задачі;
- Виберіть невідому величину, яка зазвичай позначається х;
- Результат аналізу змісту задачі відобразіть у скороченому (схематичному) записі умови задачі.
Якщо вчитель організовує колективну роботу із засвоєння змісту, то доцільним є діалог, який відбудеться після прочитання умови задачі. [29]
Наведемо приклад:
Задача 1. Насос може викачати з басейну ![]() води за 7,5 хв.
води за 7,5 хв.
Пропрацювавши 0,15 год, насос зупинився. Знайти об’єм басейну, якщо після зупинки насоса в басейні ще залишилося 25 м3 води.
Діалог з учнями може бути такий:
- Про що йдеться в задачі? (про роботу насоса);
- Про які величини йдеться в умові задачі? (про об’єм басейна та час роботи насоса);
-
Скільки води може викачати насос за 7,5 хв.? (
 об’єму води);
об’єму води);
- Скільки пропрацював насос до зупинки? (0,15 год);
- Скільки води залишилося в басейні після зупинки насоса? (25 м3 води);
Що запитується в задачі? (який об’єм басейну).
Засвоєнню умови задачі, особливо учнями, які краще сприймають
інформацію візуально, сприяє скорочений схематичний запис умови задачі, який може виконуватися навіть під час читання задачі. Форма його має бути компактною, досить наочною і зручною для сприйняття, в ній відображається тільки те, що необхідне для розв’язування. Мета таких записів – полегшити учням розуміння умови задачі, допомогти усвідомити залежність між даними і шуканими величинами. Скорочений запис умови може бути подано у вигляді графічної схеми, малюнка, ілюстрації, графіка, таблиці, графа тощо. Але короткий запис не може зводитися до переписування умови за допомогою скорочення кожного слова. Скорочений запис не самоціль, а допоміжний засіб у засвоєнні змісту та розв’язуванні задач, тому не варто насаджувати штучно певні форми коротких записів і вимагати обов’язкового їх виконання. Не до кожної задачі взагалі варто зробити схематичний запис умови. Це не може бути обов’язковою вимогою до розв’язування.[35].
Засвоєння змісту та його скорочений (схематичний) запис необхідний для того, щоб усвідомивши умову задачі, ефективно здійснити пошук рівняння (системи рівнянь). Навчаючи учнів розв’язувати сюжетні задачі складанням рівнянь, варто знайомити їх з певною системою орієнтирів, необхідних для ефективного пошуку рівняння. Ця система орієнтирів може бути представлена у вигляді евристичної схеми пошуку, яку вчитель надає учням у вигляді зразка дій, одночасно показуючи процес розв’язання задачі на основі цієї схеми. Учні можуть також скласти схему самі під керівництвом учителя, проаналізувавши розв’язання вже розв’язаної колективної задачі.
У методиці навчання математики відомі дві евристичні схеми пошуку рівняння до сюжетної задачі, з якими варто ознайомити учнів. Першу застосовують до розв’язування нескладних задач, і вона має такий вигляд:
- Позначте через х шукану величину (або одну із шуканих величин);
- Виразіть через х інші величини, про які йдеться в задачі;
- Складіть рівняння, спираючись на залежність між відомими і невідомими величинами.[50]
Друга евристична схема зручна для розв’язування складніших задач. Вона передбачає такі етапи:
- Виберіть основне невідоме і позначте цого буквою ( як правило х)
- Виразіть через х інші невідомі, про які йдеться в задачі;
- Утворіть два вирази, які відповідно до умови задачі перебувають у відношенні «більше», «менше» або «дорівнює»
- Запишіть це відношення за допомогою рівняння. [55]
Звичайно, не до кожної сюжетної задачі можна скласти рівняння, діючи відповідно до цих евристичних схем. Але для більшості задач з шкільних підручників вони є ефективними. Для задач, розв'язання яких потребує суто евристичних методів пошуку, підготовленішим учням необхідно показати інші прийоми пошуку, а саме цілеспрямованих проб; складання графів різного рівня, складання серії допоміжних задач тощо.
Ефективне розв'язування більшості задач залежить від вдалого вибору невідомих. Учнів потрібно зорієнтувати на те, що:
- за основне невідоме, як правило, зручніше вибирати меншу з шуканих величин, тоді інші невідомі виражаються через основне за допомогою дій додавання або множення;
- вибрана невідома величина не обов'язково має збігатися з величиною, яку потрібно знайти;
- невідомі треба вводити так, щоб через них було легко записати умову задачі;
- ключова фраза, з якої починається розв'язування сюжетної задачі, має бути така: „Нехай х—...”.[18]
Проілюструємо другу евристичну схему пошуку рівняння на прикладі
задачі 1.
- Виберіть основне невідоме і позначте його буквою х. Нехай х м3- об'єм бассейну
- Виразіть через х інші невідомі, про які йдеться в задачі:
![]() м3 – кількість води, яку викачає насос за 7,5 хвилини, отже, продуктивність насосу дорівнює
м3 – кількість води, яку викачає насос за 7,5 хвилини, отже, продуктивність насосу дорівнює ![]() . ( перед розв’язуванням цієї задачі варто нагадати учням поняття продуктивності).
. ( перед розв’язуванням цієї задачі варто нагадати учням поняття продуктивності).
- Утворіть два вирази, які відповідно до умови задачі перебувають у відношенні «більше», «менше» або «дорівнює»:
- За 0,15 год, що дорівнює 9 хв, тобто до зупинки, насос викачав –
![]() води
води
- після зупинки насоса в басейні залишилось 25 м3 води, отже, до зупинки насос викачав (х - 25) м3.
- Запишіть це співвідношення за допомогою рівняння:
Оскільки за умовою задачі утворені вирази — ![]() і ( х – 25) позначають
і ( х – 25) позначають
однакову кількість викачаної води до зупинки насоса, то це можна записати у вигляді рівняння:
![]() =х-25
=х-25
Обґрунтовування складеного рівняння — обов'язковий і досить важливий момент при розв'язуванні текстової задачі. У класі, де переважають підготовлені учні, одну і ту саму задачу бажано розв’язувати, складаючи різні рівняння, вибираючи за невідомі різні величини, що входять в умову задачі. Це допомагає учням краще усвідомлювати та мотивувати складене рівняння. Дуже важливі при цьому зразки міркувань, які наводить сам учитель.
Важливим при навчанні розв'язувати сюжетні задачі є засвоєння учнями певних рекомендацій, яких варто дотримуватися, розв'язуючи певні типи задач, наприклад на рух, сумісну роботу, сплави і суміші тощо. [72]
Зауважимо, що кожну арифметичну задачу можна розв’язати алгебраїчним способом за допомогою рівнянь і систем рівнянь, оскільки арифметичні методи розв’язування багатьох текстових задач на обчислення, які зводяться до лінійних рівнянь з однією змінною, часто дуже нераціональні.
В той же час, за допомогою рівнянь легко розв’язується багато задач, які з великими труднощами або навіть зовсім не можуть бути розв’язані арифметично. До того ж, арифметичне розв’язання звичайно буває дуже складним і громіздким. Приклади розв’язання за допомогою рівнянь деяких нескладних задач.
Задача 2. Для класу були заготовлені зошити. Коли роздали 48 зошитів, то їх залишилося 32 штуки. Скільки зошитів було заготовлено?
Складемо рівняння за умовою задачі. Число заготовлених зошитів позначимо через х. Коли роздали 48 зошитів, то їх запас зменшився на 48, тобто зошитів стало (х-48)
Але в задачі сказано, що зошитів залишилось 32. Отже, залишок (х-48) повинен дорівнювати 32, тобто х-48 = 32.
Розв’яжемо це рівняння. Невідоме число - зменшуване, воно дорівнює від’ємнику, доданому до різниці. Отже,
х = 48+32, або х = 80
Перевірка: 80-48 = 32.
Виникає запитання: що означатиме від’ємне число, якщо його дістанемо в результаті розв’язування задачі?
Розглянемо кілька задач.
Задача 3. Я задумав число. Коли додав до нього 27 і результат поділив на 6, то дістав 3. Яке число я задумав?
- Позначимо задумане число через х.
- Додавши до нього 27, дістанемо х + 27.
- Поділивши результат на 6, дістанемо (х + 27): 6
- За умовою задачі в результаті моє бути 3. Отже, (х+27):6 = З
- Розв’яжемо це рівняння. Знайдемо х+27 як невідоме ділене: х + 27 = 18.
Тепер знайдемо х як невідомий доданок:
х = 18-27;
х =-9
- Перевіримо підстановкою: -9 + 27 = 18
Отже, тут число -9 є відповіддю на запитання задачі. Від’ємні числа тут є допустимими значеннями для невідомого.
Задача 4. Скільки срібла 500-ї проби і 800-ї проби треба сплавити, щоб дістати 240 г 700-ї проби?
Розв’язання
Якщо 500-ї проби - х, а 800 - ї проби - у, необхідно 240г - 700-ї проби.
- Наскільки більше чистого срібла в 1 кг 700-ї проби, ніж в 1 кг 500-ї проби?
700 - 500 = 200 (г)
- Наскільки менше чистого срібла в 1 кг 700-ї проби, ніж в 1 кг 800-ї проби?
800 - 700 = 100 (г).
Тепер можна скласти таке відношення
х: у = 100:200 = 1:2 х
Розділивши 240 г в такому відношенні, матимемо
х= 80г, у = 160г
Звичайно, навчити кожного учня розв’язувати будь-яку математичну задачу неможливо, адже розв’язування більшості з них не має загальних алгоритмів. Проте для багатьох видів алгебраїчних задач такі алгоритми існують, і завдання вчителя - навчити учнів розв’язувати найважливіші з цих задач.
Але не слід забувати, що переважна більшість (понад 90%) задач, передбачених шкільною програмою, - це типові задачі. Тому вчитель насамперед повинен навчити учнів розв’язувати саме такі задачі. [2]
Добре навчити учнів можна, тільки працюючи за певною системою. Цього вимагає і принцип систематичності навчання. Якщо пропонувати їм задачі без будь-якої системи, таке навчання не сприятиме досягненню мети. Це не означає, що всі задачі треба згрупувати за якимись окремими типами і пропонувати учням спочатку задачі одного типу, потім - другого і т.д. Говорячи про систематизацію задач, ми маємо на увазі таке: якщо вчитель ознайомлює учнів з якимось новим типом задач, він повинен спочатку дати їм кілька задач тільки цього типу. Коли учні засвоять особливості їхнього розв’язування, він може запропонувати задачі цього та інших типів{24,75].
Для того щоб учні добре розв’язували текстові задачі, треба давати їм більше задач на з’ясовування залежності між величинами, особливо задач з найпростішими числовими даними, щоб виконання обчислень займало якнайменше часу й енергії. Такі задачі можна розв’язувати й усно. Наприклад, учням початкової школи для усного розв’язування доцільного запропонувати такі задачі:
- Автобус рухається з швидкістю 60 км/год.Скільки кілометрів він проїде за З год?
- Потяг за півгодини пройшов 42 км. З якою швидкістю він рухався?
Якщо на кожному уроці математики протягом тижня вони розв’язуватимуть усно по 3-5 таких задач, що поступово ускладнюються, то для них не становитимуть непереборних труднощів і складніші задачі на рух.
Розглянемо задачі, що розв’язуються методом зображення натуральних чисел у вигляді відрізків, наприклад :
Задача 5. В саду росте яблунь на 2 більше, ніж груш. Скільки в саду груш, якщо усіх дерев разом 18?
Аналіз умови.
Скористаємося схематичним малюнком. Позначимо кількість яблунь довшим відрізком, а кількість груш - коротшим (рис. 1).
![]() _____________________
_____________________
![]() ______________ 18 груш
______________ 18 груш
2 груші
Рис.1
З малюнка видно, що якщо від кількості яблунь відняти 2 дерева, то їх з грушами стане порівну. Але тоді усіх дерев разом теж стане менше на 2. Розв’язання
18-2=16 (д.) - стільки було б дерев, якби яблунь і груш було порівну.
16:2=8 (д.) - стільки було груш.
8+2=10 (д.) - стільки було яблунь.
Це задача на знаходження невідомого за різницею і сумою.
Задача 6. Певна кількість учнів пішла в кіно. Якщо зібрати з кожного учня
![]() по 20 коп. за квиток, то для купівлі квитків не вистачить 50 коп., а якщо зібрати по 26 коп., то залишиться 10 коп. Скільки було учнів? (рис.2).
по 20 коп. за квиток, то для купівлі квитків не вистачить 50 коп., а якщо зібрати по 26 коп., то залишиться 10 коп. Скільки було учнів? (рис.2).
![]()
А Д С В
Рис.2
Відрізок АВ зображає дійсну вартість усіх квитків, якщо кожний відрізок АД - вартість усіх квитків. Якщо кожний квиток коштує 20 коп., АС - вартість усіх квитків, якщо кожний квиток коштує 26 коп.
Розв’язання.
- На скільки більша вартість квитків, куплених по 26 коп., ніж вартість квитків по 20 коп.?
50коп. + 10 коп. = 60коп.
- На скільки дорожче коштує один квиток по 26коп., ніж один квиток по 20коп.?
26коп. = 20коп. = 6коп.
- Скільки було учнів?
60:6=10 (учнів).
- 20коп. * 10 = 2 грн.
- 2 грн. + 50 коп. = 2 грн.5О коп.
- 26коп. * 10 = 2 грн.60 коп.
- 2 грн.60 коп. - 2 грн.5О коп. = 10 коп.
Відповідь: 10 учнів.
Це задача на обчислення невідомого за двома різницями.
Серед задач, щo розв’язуються таким методом, виділяються дві групи. До першої входять задачі, де один із доданків на... більше (менше), ніж другий. Для їх розв’язання треба спочатку зрівняти доданки: до значення суми додати (чи відняти) значення різниці між доданками. Потім необхідно значення суми урівнених доданків розділити на 2 — знайдемо один із доданків, а потім, за умовою задачі, знайдемо другий доданок. [52]
Задача 7. У Петра та Сергія разом було 20 марок. У Сергія було на 4 марки більше, ніж у Петра. Скільки марок було у кожного з хлопців?
Розв'язання.
Урівняємо марки Сергія з марками Петра: 20-4=16 марок — разом, якщо у Сергія та Петра їх є в рівній кількості. Потім 16 розділимо на 2 — 8 марок у Петра, отже, у Сергія, за умовою задачі, 8+4=12 марок. Перевіримо: 8+12=20 марок у них разом. Можна урівняти марки Петра з марками Сергія: 20+4=24, потім 24:2=12 — марки Сергія, а Петра, відповідно, 12-4=8.
До другої групи входять задачі, де один із доданків в ... разів більше (менше), ніж інший. Для розв'язання цих задач треба кількісне значення того доданка, який менший, прийняти за одну частину, потім знайти в частинах значення інших доданків. Сума частин відповідатиме кількісному значенню суми доданків. Далі знаходимо одну частину, тобто менший з доданків, потім, за умовою задачі, інші доданки, наприклад як у задачі 7:
У Петра та Сергія разом було 20 марок. У Сергія було в 4 рази марок більше, ніж у Петра. Скільки марок було у коленого з хлопців?
Розв'язання.
У Петра менше марок, ніж у Сергія. Нехай у Петра — І частина марок, тоді у Сергія — 1-4=4 частини. Разом у них: 1+4=5 частин — їм відповідає 20 марок. .Якщо 5 частин — 20 марок, тоді 1 частина — 20:5=4 марки — у Петра. Отже, за умовою задачі, у Сергія 4-4=16 марок. Перевіримо: 4+16=20 марок у них разом.
Задача 8. В саду росте 10 яблунь. їх на 2 дерева бульиіе ніж груш. Скільки груш росте в саду?
Аналіз умови.
Це проста задача, умова якої задана неявно. Спочатку треба звернути увагу на те, що якщо яблунь більше на 2, то груш менше на 2. Отже, це задача на зменшення числа на 2 одиниці.
Розв'язання: 10-2=8 (груш)
У п’ятому класі необхідно повторити з учнями способи розв’язування таких простих задач, а вже потім переходити до розв’язування складених задач різних типів, поступово їх ускладнюючи.
Поняття текстової задачі є невідсмною частиною сучасної математики. Знання та вміння класифікувати текстові задачі значно допомагає вчителям у роботі. Адже, як було сказано раніше, кожний об’єкт математики мас свої особливості. А математика і займається тим, що встановлює для багатьох видів задач правила, користуючись якими можна знайти вказану послідовність кроків для розв’язування будь-якої задачі даного виду.
В даному розділі з’ясовано суть, типову класифікацію текстових задач та способи їх розвязуваня. Нагадаємо, що суть текстової задачі полягає в тому, що у найширшому плані вона передбачає необхідність свідомого пошуку відповідних засобів для досягнення мети, яку добре видно, але яка безпосередньо недосяжна, а у психологічному аспекті задача розглядається як свідома мета, що існує в певних умовах, а дії - як проце, спрямовані на досягнення мети. Класифікують текстові задачі по характеру об’єктів та по відношенню до теорії. Також, нами з’ясовано, що основними способами розв’язування текстових задач є аналітичний та синтетичний.
Отже, можна зробити висновок, що для багатьох видів задач правила вже давно знайдені. Правила, користуючись якими можна знайти послідовність кроків для розв’язування будь-якої задачі деякого виду, в математиці викладається в різних формах.
РОЗДІЛ 2
МЕТОДИЧНІ ПРИЙОМИ РОЗВЯЗУВАННЯ ЗАДАЧ РІЗНИХ ТИПІВ
1. Задачі на рух
У 5 класі розв'язуються задачі на рух двох типів: на зустрічний рух і на рух в одному напрямі. В разі розв'язування задач на зустрічний рух, де вимагається визначити час, через який рухомі об'єкти зустрінуться, треба додати їхні швидкості і розділити відстань між пунктами, від яких почався рух, на сумарну швидкість.
У задачах на рух, де об'єкти рухаються від одного пункту і в одному напрямі, а вимагається визначити відстань між об'єктами через певний час, раціональнішим є спосіб розв'язування, за якого знаходять різницю між швидкостями об’єктів і множать її на заданий час.
Конкретніше, при розв’язуванні таких задач роблять такі припущення:
- Якщо немає спеціальних вказівок, то рух вважають рівномірним.
- Швидкість вважається величиною додатною.
- Всі переходи на новий режим руху, на новий напрям руху вважаються такими, що здійснюється миттєво (тобто, якщо сказано, що автомобіль доїхав до пункту В, а потім поїхав назад у пункт А, то час розвороту не враховується).
- Якщо тіло має власну швидкість X і рухається по річці, швидкість течії якої дорівнює У, то швидкість тіла за течією вважається рівною Х+У, а швидкість тіла проти течії - Х-У.
- За невідоме слід приймати швидкість, а рівняння складати по рівності шляхів або рівності часу.[64,77]
В будь яких задачах на рух фігурують 3 величини:
- S - пройдений тілом шлях;
- V- швидкість руху тіла;
- t - час руху тіла.
Усі три величини пов’язані між собою формулою
S= v*t
Звідси ![]()
Розв’язуючи задачі на рух, варто пропонувати учням записувати коротку умову та здійснювати пошук рівняння, використовуючи таблицю, що пов'язує величини (шлях, швидкість, час), які характеризують рівномірний рух. Ця таблиця допомагає візуально сприйняти умову задачі, залежність між основними величинами, про які йдеться, та ефективніше здійснити пошук рівняння. Наведемо приклад. [39]
Задача 9. З пунктів А і С до пункту В виїхали одночасно два вершники і, незважаючи на те, що пункт С був на 20 км далі від пункту В ніж пункт А, вершники прибули в пункт В одночасно. Знайти відстань від пункту С до В, якщо вершник, який виїхав з С, проїжджав кожний кілометр на 1 хв 15 с швидше, ніж вершник, який виїжав з пункту А. Вершник з пункту А прибув у пункт В через 5год.
Якщо задачу розв'язують колективно в класі, то заповнення таблиці 1 може відбуватися в процесі такого діалогу вчителя з учнями:
|
|
S, км |
V, км /год |
t, год |
|
Рух вершника з А в В
|
X |
|
5 |
|
1 |
|
|
|
|
Рух вершника з С в В |
х + 20 |
|
5 |
|
1 |
|
|
- Про що йдеться в умові задачі?- Про рух вершників.
- Про які величини йдеться?- Шлях, швидкість, час.
- На скільки шлях з С до В довший ніж з А до В ?- На 20 км.
- Скільки часу кожен з вершників був у дорозі?- 5 годин.
- Що позначимо за х ?- Відстань між пунктами А і В.
- Тоді яка відстань між С і В?- Відстань між С і В (х + 20) км.
-
Як знайти швидкість вершника, що рухався з А до В ? - Щоб знайти швидкість вершника, що рухався з А до В, треба х км поділити на час руху, тоото 5 годин, отримаємо:
 км/год.
км/год.
-
Яка швидкість вершника, що рухався з С до В?- Швидкість вершника, що рухався з С до В
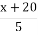 км/год.
км/год.
-
За який час вершник, що рухався з А до В, проїжджав 1 км?- Вершник, що рухався з А до В, проїжджав 1 км за:
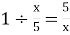 год.
год.
-
За який час вершник, що рухався з С до В, проїжджав за 1 км? – Вершник, що рухався з С до В, проїжджав 1 км за:
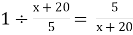 год.
год.
-
Запишіть за допомогою рівності співвідношення між величинами
 і
і 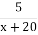 , виходячи з умови задачі.
, виходячи з умови задачі.
-
Оскільки, за умовою задачі, час, записаний виразом
 , на 1 хв 15 с, що дорівнює
, на 1 хв 15 с, що дорівнює 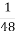 години, більший, ніж час, записаний виразом
години, більший, ніж час, записаний виразом 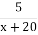 , то неможна записати у вигляді рівняння
, то неможна записати у вигляді рівняння  -
- 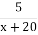 =
= 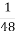 .
.
Таблицю варто застосовувати не тільки розв’язуючи задачі на рух. Взагалі таблиця у багатьох випадках систематизує та візуалізує умову задачі, пошук її рівняння і цим оптимізує розв’язування задачі. Наведемо приклад.
Задача 10. У трьох бідонах разом було 50 літрів молока. У першому було на 10 літрів більше, ніж у другому. Коли з першого бідона вилили у третій 26л, тo у другому і третьому бідонах молока стало порівну. Скільки молока було у другому бідоні спочатку?
Оскільки, за умовою задачі, після переливания у другому і третьому бідонах молока стало порівну, то це можна записати у вигляді рівняння:
66-2х=х
|
|
Перший бідон, л |
Другий Бідон,л |
Третій бідон, л |
|
Було до переливання |
х+10 |
X |
50-х-(х + 10) = 40-2х |
|
Стало після переливання |
х+10-26 |
X |
50 - х - (х +10) + 26 = 66 - 2х |
2.Задачі на змішування
Окремо треба спинитися на так званих задачах на змішування (суміші, розчини сплави), які досить часто зустрічаються на практиці, а також під час вивчення хімії, фізики.
Умовно розрізняють два види задач на змішування:
- задачі на змішування першого роду;
- задачі на змішування другого роду.
Найхарактернішими задачами на змішування першого роду є задачі на знаходження середньої ціни, середньої температури, середньої швидкості, середнього часу та ін. У цих задачах треба визначити „ціну" суміші за даними „цінами" і кількостями окремих сортів. Отже, мова йде про знаходження середнього арифметичного певної суми доданків, узятих групами. Шуканим може бути не лише середнє арифметичне, а й ціна одного з сортів.[2]
Задача 11. Купили 50 кг картоплі першого сорту по 24 к. за кілограм і 150 кг картоплі другого сорту по нижчій ціні. Середня ціна картоплі дорівнювала 19,5 к. Визначити ціну картоплі другого сорту.
Розв’язання:
Нехай х - ціна картоплі другого сорту. Тоді для розв’язування задачі складаємо рівняння
![]()
У задачах на змішування другого роду найчастіше відомі „ціни" окремих сортів, „ціна” та кількість суміші, а треба визначити кількість взятих для суміші сортів.
Задача 12. Один кілограм товару першого сорту коштує 7,2 гри, а один кілограм іншого товару коштує 8,4 грн. Скільки кілограмів товару кожного сорту треба взяти, щоб вийшло 120 кг суміші, кожний кілограм якої коштує 7,5 крб.?
Розвязання:
Нехай x (кг) - маса товару першого сорту, тоді за умовою задачі маса товару другого сорту буде (120 - х). Складаємо рівняння.
![]()
Задачі на змішування за своїм фізичним змістом можна розподілити на підгрупи, кожна з яких потребує певних додаткових пояснень. Розглянемо ці підгрупи:
- задачі на розчини;
- задачі на сплави.
Задачі на розчини
В умовах задач на розчини фігурує термін „концентрація". Необхідно пояснити учням зміст цього поняття. Якщо т -маса розчину, п –маса розчиненої
речовини, то відношення ![]() , подане в процентах, називають концентрацією розчину.
, подане в процентах, називають концентрацією розчину.
Якщо позначити концентрацію буквою С, то для її визначення можна скористатися формулою ![]() 100
100
Концентрацію розчину можна виразити не тільки в процентах, а й у частинах. Кажуть, наприклад, що концентрація солі у морській воді дорівнює ![]() ( за масою).
( за масою).
Для зручності розв'язування задач на розчини можна користуватися формулою, яку неважко вивести. [32]
Нехай маємо два розчини однієї і тієї самої речовини. Концентрація першого розчину дорівнює С1, а його масса m1 ; відповідно для другого розчину
С2 і m2. Важливо підкреслити, що m1 і m2 мають бути в одних і тих самих одиницях.
За формулою ![]() 100 знаходимо масу речовини в розчині:
100 знаходимо масу речовини в розчині: ![]() .
.
Маса речовини в першому розчині: ![]() C1 у другому розчині:
C1 у другому розчині: ![]() C2
C2
Отже, у розчині масою m1+m2, маса речовини становить ![]() C1+
C1+ ![]() C2, тобто концентрація С суміші дорівнює
C2, тобто концентрація С суміші дорівнює
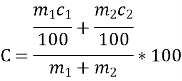
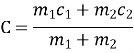
Зауваження. Концентрація суміші, утвореної з k розчинів однієї й тієї самої речовини, обчислюється за формулою:
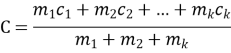
Під час розв'язування задач не обов'язково користуватися готовою формулою. Можна поступово виконувати розрахунки, пов'язані з визначенням маси розчину і маси розчиненої речовини, і користуватися поняттям концентрації. [31]
Задача 13. У посудині 10,5 л 40%-ного розчину сірчаної кислоти. Скільки треба влити в посудину 75%-ного розчину тієї самої кислоти, щоб вийшов 50%- ний розчин?
Розв'язання.
Позначивши через х л шуканий об'єм 75%-ного розчину кислоти, складаємо рівняння.
![]()
Звідки х=4,2л
Зауваження. Розв'язуючи задачі на концентрацію кислот і сплавів, треба пояснити учням, що міцність кислоти або спирту звичайно виражається в сотих долях, або процентах, які в цьому випадку називають градусами.
Задача 14. Змішали 30%-иий розчин соляної кислоти з 10%-ним її розчином і дістали 600 г 15%-ного розчину. Скільки грамів кожного розчину було взято?
Розв’язання.
1-ий спосіб. Нехай х г — маса 30%-ного розчину кислоти, a
y — маса 10%-ного розчину кислоти. Для визначення значення х і у складаємо систему:
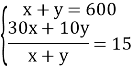
звідки х = 150г, у = 450 г.
2-ий спосіб.

За малюнком складаємо рівняння (систему)
![]()
Розв’язавши цю систему отримуємо, що х = 150 г, у = 450 г.
Сплав можна розглядати як розчин, у якому один з компонентів (довільний) є розчинник, а другий розчинна речовина.
Задача 15. 1см3 одного металу важить 7,2 г, а 1см3 іншого металу важить 8,4 г. Скільки кубічних сантиметрів кожного металу треба взяти, щоб дістати 1500 см сплаву, кожний кубічний сантиметр якого важить 7,5 г?
Розв’язання.
Нехай для утворення сплаву треба взяти х см3 одного металу і у см3 іншого металу. Складаємо систему рівнянь.
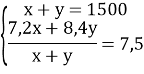
звідки х = 1125г, у = 375г.
Розв’язуючи деякі задачі на сплави і суміші, треба пам’ятати про ключове питання: Яка речовина залишається незмінною за масою?
Задача 16. Кусок сплаву міді і цинку масою в 36 кг містить 45 % міді. Яку масу міді потрібно додати до цього шматка, щоб новий сплав містив 60% міді?
Колективний пошук рівняння може відбуватися в процесі такого діалогу вчителя з класом:
- Які речовини містить сплав? Сплав містить мідь і цинк.
- Яка речовина незмінна за масою в обох сплавах? В обох сплавах незмінним за масою є цинк.
- Який процентний вміст цинку в початковому сплаві? У початковому сплаві 100 % — 45 % = 55 % цинку.
- Скільки кг цинку в початковому сплаві? У початковому сплаві
36*0.55 = 19.8 кг цинку.
- Скільки кг цинку в новому сплаві? У новому сплаві цинку теж 19,8кг.
- Що позначимо за х ? Нехай х кг — маса міді, яку додали до нового сплаву.
- Тоді яка загальна маса нового сплаву? Загальна маса нового сплаву (36+х) кг.
- Скільки всього кг міді в новому сплаві? У новому сплаві
- х – 19,8= 16,2 +х – кг міді.
- Скільки кг становить мідь від загальної маси нового сплаву? 60 % міді від загальної маси нового сплаву становить 0,6(36 +х) кг.
- Запишіть за допомогою рівності співвідношення між виразами
(16,2 + х) і 0,6(36 + х), виходячи з умови задачі.
- Оскільки, за умовою задачі, утворені вирази ( 16,2+х) і 0,6 ( 36+х) позначають одну і ту саму масу міді у новому сплаві, то це можна записати у вигляді рівняння: 16,2+х = 0,6(36+х)
Розв’язавши складене рівняння, необхідно здійснити перевірку відповідності знайдених коренів рівняння умов задачі. Це пов’язано з тим, що рівняння, яке складається під час розв’язування сюжетної задачі, не враховує обмеження на реально існуючі фізичні величини, які фігурують в умові задачі. Наприклад, кількість учнів у класі або кількість працюючих робітників має бути натуральним числом, об’єм певної ємкості - додатним числом і т.д. При цьому зрозуміло, шо такі обмеження існують не тільки для змінної х, відносно якої розв'язується рівняння; а й на інші величини, що розглядаються в процесі складання рівняння. Саме тому не всі корені одержаного рівняння можуть бути розв'язками задачі. Перевірка відповідності знайдених коренів рівняння умові задачі нерідко може виконуватись і усно. Суть перевірки така: взявши кожен знайдений корінь рівняння, обчислюємо всі величини, що входять до умови задачі, і перевіряємо, чи задовольняють вони фізичні обмеження реальних процесів та явищ. Якщо ж хоч на одному етані є невідиовідпість, то такий корінь рівняння не повинен вважатися розв'язком задачі.[22|
Таким чином, для перевірки кореня рівняння досить переглянути умову задачі від початку до кінця, обчислюючи всі величини, що входять до умови, слідкуючи за виконанням фізичних та змістових обмежень. Для прикладу повернемося до задачі 10. Розв'язавши одержане рівняння 66 – 2х = х, отримаємо корінь х =22 . На перший погляд, цей корінь рівняння можна вважати розв'язком задачі (адже 22 — число додатне, тобто у другому бідоні було 22 літри молока). Але оскільки фабула сюжетної задачі відображає певну життєву ситуацію, то зрозуміло, що не тільки остаточна відповідь, а й усі проміжні дані задачі мають бути реальними, тобто що стосується цієї задачі — об’єм молока у всіх бідонах і до і після переливання має бути додатним числом. Пройшовши рядками таблиці, ми бачимо: якщо х = 22, то до переливання в першому бідоні було 32 літри молока, у другому 22, а у третьому молока було 50–32–22=-4 літри ( число від’ємне). Чого, зазвичай, за змістом цієї фізичної величини в реальній ситуації бути не може. Таким чином, знайдений корінь рівняння х=22 не є розв'язком задачі. Тобто задача розв'язку не має. Якщо вважати, що сюжетна задача відображає ситуацію, близьку до життєвої, практичної, де дається опис кількісної хороші реального явища чи події, то і розв'язок, і всі знайдені проміжні величини в ній мають відповідати реальній ситуації. Хоч у класах з поглибленим вивченням математики, де розглядають елементи математичної логіки, міркування стосовно хибних даних задачі можуть бути доречними. В загальноосвітніх класах числові дані в задачах варто добирати так, щоб уникати подібної ситуації у величинах, що виражаються як проміжні або допоміжні, і під час перевірки зосереджувати увагу на відповідності знайдених коренів рівняння умові задачі. В остаточній відповіді сюжетної задачі знайдена невідома величина має бути реальною з фізичного погляду, не суперечити життєвому
досвіду учнів.[54,73]
Щодо запису розв'язання задачі в зошитах учнів, то він мас бути лаконічним і відображати:
- вибір і позначення основної невідомої величини;
- подання решти невідомих величин через основну невідому;
- обгрунтування складеного рівняння;
- розв'язання рівняння;
- перевірку відповідності знайдених коренів рівняння умові задачі;
- запис відповіді.
3.Диференційоване навчання розв’язуванню задач
У середній школі диференційоване навчання відоме досить давно. Так, до недавнього часу в школі була єдина програма і єдиний навчальний план. А вчитель здійснював диференційований підхід, спираючись, головним чином на індивідуальні особливості розумової діяльності дітей та особисту якість навчання. Це було названо “внутрішньою диференціацією”.
Початківці в умовах одного класу, при наповненні 25-30 і більше учнів, виділяють групи дітей з більш-менш однаковими здібностями. Безумовно, коли такі групи учнів постійні, вчителю легко з ними працювати, застосовуючи до кожної з них різні методи і прийоми навчання. Але протягом навчального року ці групи змінюються. Так, один учень на початку навчального року може бути в групі слабких, а через 3-4 місяці наздогнати групу сильних дітей і навпаки.
Традиційно на етапі закріплення знань і умінь основою диференційованого підходу є самостійна робота. Якраз тут ми й маємо більше можливостей для врахування індивідуальних особливостей дітей. Наприклад, учитель готує 2-3 варіанти диференційованих завдань і пропонує виконати певній групі школярів той чи інший з них. Різновиди ж завдань, коли учні самі можуть добирати варіанти роботи, часто мають негативні сторони: слабкий учень, у переважній більшості, вибирає собі завдання не за здібностями і не виконує його. Результат - незадовільна оцінка. Сильний учень також вибирає завдання, але простіше і швидко його виконує, без зусиль. Результат - відмінна оцінка, але розумова діяльність цього учня не отримала відповідного навантаження. [5]
Існують інші способи диференціювання завдань, описані М.В. Богдановичем. Це диференціювання з елементами допомоги. Вчений пропонує різні способи допомоги, тобто для розв'язування задачі даються:
- зразок виконання;
- план чи схема розв'язування;
- конкретизація завдань;
- інформація, необхідна для виконання;
- сповіщення початку розв’язування задачі та ін.[4]
Ми пропонуємо розглянути спосіб диференціювання, який можна умовно
назвати ускладненням змісту на основі додаткових завдань. Цей спосіб розкриваємо на прикладі роботи з текстовими задачами. Відомо, що текстові задачі складають близько 40% навчального матеріалу з математики. На їх розв'язування витрачається значна частина навчального часу.
Але аналіз якості навчання з математики під час щорічних перевірок у школі свідчить про невміння значної частини учнів розв'язувати текстові задачі.
Вивчення досвіду масової школи переконує, що вчителі-практики під час розв’язування задач орієнтують учнів на досягнення єдиної мети - отримання результату (відповіді задачі). І лише невелика кількість практиків проводить додаткову роботу над деякими уже розв'язаними задачами, про що свідчать результати анкетування.
Так, аналізуючи відповіді на запитання «Чому не проводиться диференційована робота над задачею, яку розв'язали?», ми дізналися, що деякі вчителі - 13% - не вважають цю роботу за потрібну, у інших-29% опитаних- просто не вистачає часу (вважаємо, що ця частина вчителів-практиків не вміє правильно розподіляти час на уроці), треті (26%) пояснюють це тим, шо вони намагаються за урок розв'язати з дітьми 2-3 задачі, запропоновані підручником на диференціювання завдань до задачі «не доходять руки», решта респондентів 32% - пробує здійснювати диференціювання на уроці, але не зовсім уявляє, що це таке.[74]
Ми вважаємо, що протягом уроку краще розв'язати 1-2 задачі з комплексом додаткових завдань, ніж 2-3 не пов'язаних одна з одною змістом. Ще гірше ці задачі однотипні або змінені лише назви і цифри. Чому?
По-перше, диференційовані завдання до задачі не тільки не порушують структури уроку, а й допомагають учням набувати додаткової інформації, виявляти елементи творчості, розвивати логічне мислення.
По-друге, практика свідчить, що додаткові завдання в умовах внутрішнього диференціювання класу сприяють вирішенню ще декількох важливих проблем. А саме:
- раціонально використовується навчальний час сильними учнями, і, на цій основі, розширюються та поглиблюються їхні знання;
- не занижується програмовий рівень задач;
- вилучається фальшивий поділ класу на групи, що іноді негативно впливає на психіку дитини;
- в учителя з'являється більше вільного часу для надання допомоги слабковстигаючим;
- класовод витрачає менше часу на підготовку додаткових завдань до задачі, ніж на написання набору карток в 3-4 варіанти.
Яку ж роботу ми пропонуємо?
Дається текст задачі для розв'язування. До поданої задачі вчитель складає ряд завдань, тісно пов'язаних одне з одним. Перше завдання обов'язкове для всіх
- розв'язати задачу з підручника. Наступні - перебудувати або реформувати вже розв'язану задачу. Додаткових завдань можна скласти декілька, залежно від мети уроку, труднощів самої задачі, наявності часу на уроці. Візьмемо, для прикладу, задачу.
Задача 17. В одному районі міста минулого року побудували 6 однакових будинків по 126 квартир у кожному. Цього року побудували на 240 квартир більше. Скільки сімей одержали квартири в нових будинках цього року?
- На скільки більше квартир побудували цього року, ніж минулого?
-
Скільки квартир різних типів отримали сім'ї цього року, якщо 2-кімнатні складали
 від усіх квартир, 3-кімнатні -
від усіх квартир, 3-кімнатні -  , 4-кімнатні -
, 4-кімнатні -  від двокімнатних, а решта були однокімнатні квартири?
від двокімнатних, а решта були однокімнатні квартири?
- Скільки вікон довелося зробити столярам, якщо кожна кімната і кожна кухня в квартирах мають по одному вікну?
Перебудова задачі потребує від учителя додаткових зусиль, бо в цьому випадку необхідно встановити і виявити нові зв'язки й відношення між величинами задачі, пов'язати їх між собою, скласти з їх допомогою додаткові завдання. В цьому і полягає головна трудність запропонованої роботи.
Слід зазначити, що під час складання практичних задач необхідно використовувати нормативи, подані у додатковій літературі, краєзнавчі матеріали. Важливо, щоб застосування фактів і цифрових даних було науково правильним, практично значимим, пізнавально-виховним. Додаткові завдання мають бути чітко сформульовані і посильні для самостійного виконання учнями [70]
Задача 18. 360 кг груш розклали у ящики по 12 кг і 9 кг. Ящиків по 9 кг було 8. Скільки було ящиків по 12 кг?
Розв'язання.
- 9*8 = 72 (кг) - було в 8 ящиках.
- 360-72 = 288 (кг) - було в решті ящиків.
- 288:12 = 48 (ящ.) - усього ящиків по 12 кг.
- Скільки груш продали за день, якщо було продано 15 ящиків по 12 кг і 7 ящиків по 9 кг?
12*15+9*7 = 243 (кг)
- Чи можна розкласти груші, що залишились, в ящики по 12 кг?
360-243 = 117 (кг)
117:12 = 9 (ящ.) та остача - 9 кг.
Відповідь: не можна розкласти всі ці груші в ящики по 12 кг порівну, тому що лишається ще 9 кг.
Під час проведення такої роботи обов'язкову (основну) задачу мають розв'язати всі учні класу. Додаткові завдання пропонуються також усім школярам, але починати виконувати наступне завдання можна тільки тоді, коли розв'язали попереднє. Виконання додаткових завдань має бути розраховане на середніх і сильних учнів. Слабких дітей слід залучати поступово.
Отже, застосування на практиці диференційованих завдань переконує нас у тому, що можна отримати досить добрі результати під час навчання ділей математики. Насамперед, усі без винятку учні почали успішно справлятися з обов'язковим завданням. Крім того, школярі одержали можливість перевірити свої здібності. На уроках учні не сиділи без діла, не гаяли часу, бо кожний із них намагався виконати якомога більше завдань. [70]
- етап. Спільне завдання.
Чи можна розв'язати цю задачу?
До ательє завезли 125 м тканини. З неї пошили кілька блузок, витративши на кожну З м, і кілька платтів, витративши на кожне 5 м тканини. Скільки платтів пошили в ательє?
V етап. Перевірка додаткових завдань.
VI етап. Підсумок уроку.
4.Текстові задачі в закордонних школах
Пропоную звернути увагу на думку одного з провідних російських викладачів математики, який на даний час працює за кордоном. А.Л.Тоом має досвід викладання математики в МДУ ім. М.В.Ломоносова і ФМІІІ №18 при МДУ, він автор статей та цікавих задач, які публікувалися в журналі “Квант" і в книгах для заочної математичної школи. Більше 10 років Андрій Леонович живе і працює за кордоном, викладав в університетах Італії, СІНА, Бразилії, де звернув увагу на абсолютно незвичне для нього ставлення навчаючих до використання текстових задач в процесі навчання.
В одній зі статей, опублікованих за кордоном, А.Л. Тоом пише: «Коли я приїхав в США дев'ять років тому і почав викладати, я виявив, шо багато студентів університету дуже погано справляються з вирішенням текстових задач. Коли я став читати американську освітню літературу, я виявив дивний (для мене) підхід до текстових задач, зовсім відмінний від того, до якого я звик у Росії. Схоже, що багато хто вважає, що завдання, які вирішуються на уроках математики, повинні бути якомога ближче до повсякденного життя. Я вважаю що цей підхід бере свій початок у відомого американського психолога викладача Е. Торндайка, в чиїй авторитетній книзі «Психологія алгебри» міститься глава, названа «Нереальні й марні завдання», що починається так: « У попередній главі було показано, що близько половини завдань, що даються в стандартних курсах, несправжні, оскільки в реальному житті відповідь ніколи не знадобиться. Очевидно, не варто, хіба що для об'єму, таким чином з'єднувати алгебраїчну роботу з нікчемністю ». [6]
У тій же статті А.Л. Тоом наводить приклад задачі, яка «може використовуватися мало не всюди на земній кулі без всяких обмежень:
Саллі на п'ять років старша за свого брата Білла. Через чотири роки вона буде в два рази старше, ніж тоді буде Біллу. Скільки років Саллі зараз?
Але вона оголошується непридатною з наступної причини : «Перш за все, хто б міг задати подібне запитання? Кому це може знадобитися? Якщо Білл і Саллі самі не знають, це якась дивна сім'я ».|79]
Ось ще один приклад. А.Л. Тоом наводить вислів У.Залмана про традиційні текстові задачі, опублікований в головному американському журналі для вчителів математики «Вчителі математики» (Mathematics teacher): «Алгебра має так багато справжніх додатків, що фальшиві традиційні текстові задачі більше не потрібні». <...> Чому Залман називає традиційні текстові задачі фальшивими? Він наводить задачу:
У однієї людини в гаманці 20 монет, одні по 5 центів, інші по 10 центів на загальну суму в долар і 75 центів. Скільки у нього монет по 5 центів? Скільки по 10 центів?
Потім Залман пише: «Оскільки монети були полічені, чому б не злічити окремо монети в 5 центів і окремо в 10 центів?».
У Росії (і, думаю, у величезній більшості країн) цей дивний аргумент був би залишений без уваги як невдалий жарт, але в Америці до нього ставляться з великою повагою ».
Як бачимо, не тільки в Росії спостерігається нерозуміння питання «навіщо вчити рішенню текстових задач?» Звернемо увагу і на інші аргументи зарубіжних супротивників використання текстових задач у процесі навчання. Ось звичайне для нашої початкової школи завдання.
Літак злітає і спрямовується на схід зі швидкістю 350 миль на годину. У той же час злітає інший літак і прямує на захід зі швидкістю 400 миль на годину. Коли відстань між ними досягне 2000 миль?
А.Л. Тоом відзначає, що ця задача кілька років тому була згадана в «Вчителі математики» з наступним зневажливим коментарем: «Всякий нормальний учень повинен запитати: А кому це треба? Нікому немає діла крім вчителя алгебри, що задає такі завдання, і учня, якому потрібна відмітка. Наша програма і без того занадто перевантажена, щоб включати такі чудасії».
А.Л. Тоом приводить дуже важливе спостереження-. «Складається враження, що текстові задачі майже завжди викладалися настільки погано, що більшість учнів не могли відокремити самі текстові задачі від поганої манери викладання. Ральф Реймі - один з тих, хто зумів це зробити: «Я був слухняним учнем і робив те, що мені веліли, а веліли мені поміщати певні числа в певні клітинки таблиці і робили ми це для настільки обмеженого кола завдань, що їх можна було все запам'ятати. Це йшло насилу, і згодом я зрозумів, як легкі були ці завдання, але оскільки мені говорили, як їх робити, і оскільки мене хвалили, я це й робив, без найменшого проблиску розуміння. Розуміння не виникло навіть, як це буває у вивченні іноземних мов, коли складаєш з слів пропозиції і відмінювати дієслова, поступово опановуючи мовою. З алгеброю у мене так не вийшло, і коли я здолав її згодом і побачив, якими ідіотськими були мої шкільні вправи, це сталося не завдяки таблицям, які я заповнював раніше. Біда була не в задачах, не в ідеї «типів». Біда була в викладанні ». [8]
Як бачимо, практика навчання рішенню завдань без опори на розуміння учням сенсу виконуваних ним дій була характерна не тільки Росії. Відзначимо, що А.Л. Тоом не обмежується критикою супротивників застосування текстових задач в процесі навчання. Розмірковуючи над їх «аргументами», він шукає і знаходить переконливі аргументи на користь текстових завдань, на які варто звернути увагу. Розвиваючи відомі в Росії погляди Дж. Пойа в питанні «навіщо вчити рішенню текстових задач?», він розглядає вплив навчання рішенню текстових задач на розвиток уяви учнів, на формування перших абстракцій розвиток абстрактного мислення так необхідного для навчання математики. [60]
Досвід навчання рішенню текстових завдань у зарубіжних країнах просто інший. Наприклад, учні шостих класів масових шкіл Ізраїлю вирішують, по суті не завдання, а вбрані в словесну форму приклади на виконання арифметичних дій. «В окремих випадках для вирішення потрібно виконати дві (і страшно подумати!) Три дії, - пише у приватному листі В. Романовський, але ізраїльський підручник для 6 класу ні в яке порівняння не йде з підручником серії « МДУ-школі». Його мабуть, можна порівняти з підручником Л.Г. Петерсон для 3 класу, однак і цей підручник, на мій погляд, набагато краще».
На завершення сформулюю декілька положень, щодо текстових задач
- Текстові задачі с важливим засобом навчання математики. З їх допомогою учні отримують досвід роботи з величинами, осягають взаємозв’язки між ними, отримують досвід застосування математики до вирішення практичних (або правдоподібних) завдань.
- Використання арифметичних способів вирішення завдань розвиває кмітливість, уміння ставити питання, відповідати на них, тобто розвиває природну мову, готує школярів до подальшого навчання.
- Арифметичні способи вирішення текстових завдань дозволяють розвивати вміння аналізувати задачні ситуації, будувати план рішення з урахуванням взаємозв'язків між відомими і невідомими величинами (з урахуванням типу завдання), витлумачувати результат кожної дії в рамках умови задачі, перевіряти правильність рішення за допомогою складання і розв’язання зворотної задачі, тобто формувати і розвивати важливі загальнонавчальні вміння.
- Арифметичні способи вирішення текстових завдань привчають дітей до перших абстракцій, дозволяють виховувати логічну культуру, можуть сприяти створенню сприятливого емоційного фону навчання, розвитку у школярів естетичного почуття стосовно до вирішення задачі (гарне рішення!) І вивчення математики, викликаючи інтерес спочатку до процесу пошуку рішення задачі, а потім і до досліджуваного предмета.
- Використання історичних завдань і різноманітних старовинних (арифметичних) способів їх вирішення не тільки збагачують досвід розумової діяльності учнів, але і дозволяють їм освоювати важливе культурно-історична спадщина людства, пов'язаний з пошуком рішення задач. Це важливий внутрішній (пов’язаний з предметом), а не зовнішній (пов’язаний з відмітками, заохоченнями і т.п.) стимул до пошуку рішень задач та вивченні математики.[61]
Очевидно, щo роль текстових задач в курсі математики основної школи як в Україні так і за її кордоном дуже велика. Але для того, щоб була досягнена кінцева мета навчання потрібно правильно ознайомлювати дітей з матеріалом. Вчителю потрібно звернути увагу на зміст задачі та її вирішення. Адже, якщо діти розумітимуть зміст задачі, то у них не виникатиме таких проблем як у Ральфа Реймі. [80]
ВИСНОВКИ ДО ДРУГОГО РОЗДІЛУ
В даному розділі показано методичні прийоми розв’язування різних типів текстових задач та їх особливості, вказано правильність запису розв’язаної задачі у зошиті. Також, особлива увага звертається на диференційоване навчання. Нами було проведено та проаналізовано опитування вчителів-математиків, щодо використання диференційованого навчання на уроках математики. Результати показали, що 32% вчителів хочуть використовувати таке навчання на уроках, але мало уявляють, що воно собою являє. Тому, можна зробити висновок, що поняття диференційованого навчання потребує підвищеної уваги з боку вчителів, адже воно не порушує структури уроку, а допомагає учням набувати додаткової інформації, виявляти елементи творчості, розвивате логічне мислення.
На завершення, нами було з’ясовано особливості навчання розв’язуванню текстових задач в закордонних школах. Аналіз закордонної методики значно допомагає розширенню уявлення про методику розв’язування текстових задач та уникненню пезрозумілостей з боку дитини.
ДОСЛІДЖЕННЯ ПРАКТИКИ РОБОТИ УЧНІВ І ВЧИТЕЛІВ, ЩОДО РОЗВЯЗУВАННЯ ТЕКСТОВИХ ЗАДАЧ
Нами було проведено анкетування між учнями різних класів та різних шкіл, з метою з’ясування ставлення сучасної дитини до розв’язування текстових задач.
Анкетування 5-6 класів проводилося в Наркевицькій ЗОШ І-ІІІ ступенів. У 5 класі було опитано 20 учнів, у 6 класі - 20 учнів.
Анкетування 7-8 класів проводилося в Дзеленецькій ЗОШ І-ІІ ступенів. У 7 класі було опитано 3 учнів, у 8 класі - 3 учнів.
Анкетування 9 класу проводилося вТрительницькій ЗОШ І-ІІ ступенів . У 9 класі було опитано 10 учнів.
Нас цікавив ряд запитань:
- Про частоту розв’язування текстових задач дитиною;
- Про власну самооцінку здатності розв’язати текстову задачу;
- Про знання типів задач;
- Про задачі, яким дитина надає перевагу;
- Чи любить учень відвідувати уроки математики;
- Що в математиці приваблює найбільше.
Результати показали, що розв’язуванню текстових задач приділяють достатньо увагу і вони займають одне з найголовніших місць в курсі математики основної школи. Проте, найчастіше текстові задачі розв’язуються учнями 5-6 класів. Не дивно, адже математика в 5-6 класі опирається на текстові задачі, на яких діти тренують свої обчислювальні навички. Аналіз опитування висвітлено на поданій нижче діаграмі.
Частота розв'язування текстових задач
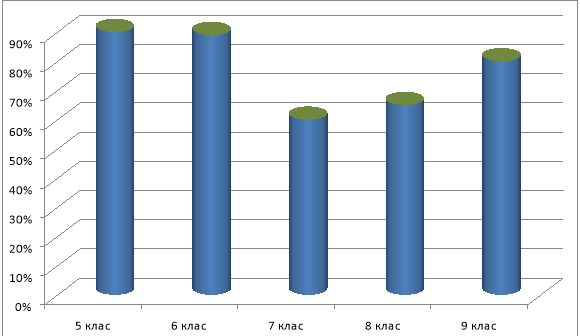
Цікавими є результати опитування учнів з приводу оцінки власних можливостей розв’язування текстових задач. Учні різних класів з впевненістю написали, що вони вміють розв’язувати текстові задачі. Лише невеликий відсоток учнів 5-6 класів (8%) написали, що не вміють працювати з даними задачами. Такий результат свідчить про гарний внутрішній розвиток школярів, їхню впевненість у собі, що є важливим з точки зору психології. Критичне ставлення дитини до себе (а саме впевненість в тому, що я не вмію) свідчить про замкненість учня. А це означає, що вчитель не зумів розкрити потенціал дитини на уроці.
На жаль, знання типів текстових задач знаходиться дуже на низькому рівні. Нами було проведено опитування між 5, 6, 7, 8 та 9 класами. Суть його заключалася в тому, щоб визначити як сучасні діти ознайомлені з типологією текстових задач і чи знають вони її взагалі. Отримані результати подані нижче в таблиці.
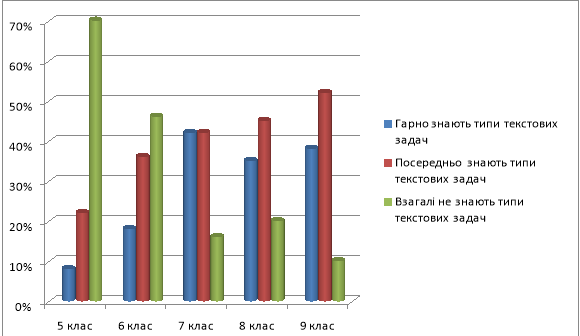
Бачимо, що незважаючи на вміння розв’язувати текстові задачі, знання типології текстових здач знаходиться на низькому рівні. Очевидно, що такий недолік потрібно доопрацьовувати, адже знання типів текстових задач допоможе швидко зорієнтуватися зі способом розв’язування задачі. Бесідуючи з учителем Трительницької ЗОШ, ми дізналися, що загалом діти завчають способи розв’язування текстових задач, опираючись на приклади, які були розглянуті на уроці. Лише учні, які додатково займаються в позакласний час добре орієнтуються в типології текстових задач. Таких учнів, па превеликий жаль, стає все менше.
Опираючись на попереднє дослідження знання типології текстових задач, було проблематичним визначити яким типам задач надають перевагу учні. Тому мною були оголошені різні типи текстових задач, а діти обирали один тип, який їм подобається найбільше. Майже всі учні різних класів найулюбленішими задачами визнали задачі на рух, лише 7 клас обрав задачі на відсотки.
Опитування стосовно відношення учнів до предмету математика загалом
подано нижче:
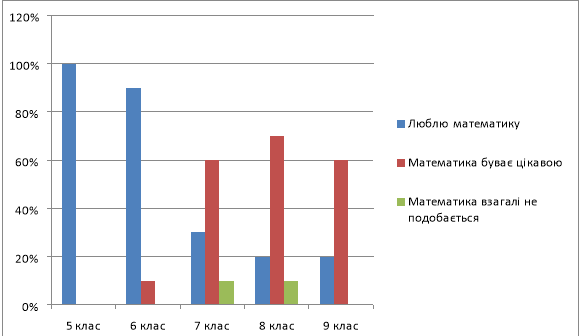
На запитання “Чому математика перестає подобатися з роками?” діти відповіли, що математика цікава до тих пір, доки зрозуміла і доки її цікаво розповідають. Коли починаються неточності в розумінні матеріалу або ж певні особливості вчителя не дозволяють йому проводити нестандартний урок- цікавість до предмету зникає, а отже і знижується рівень знань загалом.
- Методичні помилки вчителя при роботі з текстовими задачами
Надання основної ролі текстовим задачам у шкільному курсі математики є дуже гарним початком і прогнозує гарні результати навчання. Проте, ми часто зустрічаємося з тим, що більшість учнів основної школи не вміють розв’язувати текстові задачі. Звісно, потрібно брати до уваги розумові та фізіологічні здібності дитини, але загалом уся ситуація залежить від учителя, від його вміння подати інформацію та опрацювати її разом з дітьми.
Якщо педагог не вміє користуватися своїми знаннями, не вміє застосовувати їх на практиці, він починає допускати помилки, які згодом допускають і його учні. Розглянемо найтиповіші з них.
Помилка 1. Пропуск етану аналізу умови задачі.
Найперше, з чого починається розв’язування задачі, - умова. Правильний розв’язок залежить від правильності способу розв’язування, а той, у свою чергу - від правильного розуміння умови. Якщо дитина прочитала задачу і не зрозуміла або не правильно зрозуміла умову, то очевидно, що й правильного розв’язку в неї бути не може.
Дуже часто можна спостерігати картину, коли вчитель каже номер задачі, кожний учень у класі прочитує її про себе, і після цього викликається дитина, яка має розв’язати задачу на дошці. В класі можуть бути діти, які швидко проаналізували умову задачі і знають хід розв’язання. Проте не всі учні такі. Вчитель обов’язково має зробити задачу найбільш доступною та зрозумілою всім учням. Звісно, не потрібно затримувати навчальний процес заради слабших учнів. Можна розробити певну систему. Наприклад, задача читається одним із учнів на весь клас, далі всі разом аналізують умову, виділяють, що дано, що потрібно знайти та як раціональніше записати розв’язання. Після цього хтось виходить до дошки та оформляє задачу. [68]
Колективні обговорення розвивають у дітей вміння слухати інших та вміння обґрунтовувати свою думку. Під час колективного аналізу кожний з учнів не буде боятися сказати свою думку та запропонувати свою ідею, адже, як ми знаємо, дошка зазвичай лякає учнів. Якщо ж знайдуться учні, яким все одно не зрозуміло що, де і як, тоді учитель має в індивідуальному порядку пояснити дитині, адже його завдання навчати.[4]
Розглянемо такий приклад.
Задача 18. Одна труба наповнює басейн зо 10 годин, а друга – за 15 годин. За скільки годин наповнюють басейн обидві труби, працюючи разом?
|
|
Наповнюють басейн |
Разом наповнюють басейн |
|
1 труба |
10 годин |
|
|
2 труба |
15 годин |
Якщо на даному етапі не проаналізувати умову, то учні зазвичай швидко пишуть, що обидві труби наповнять басейн за 25 годин, і впевнено чекають наступної задачі. Завдання вчителя разом із дітьми проаналізувати умову. Тобто, якщо одна труба наповнює басейн 10 годин, то, включивши ще одну трубу, логічно очікувати, що басейн наповниться швидше.
Помилка 2. Пропуск етапу пошуку способу розв'язування.
Проаналізувавши умову, можна приступати і до розв’язування задачі. Постає головне питання - як знайти невідоме? Звичайно, вчитель може викликати сильнішого учня до дошки, він розв’яже задачу, і все. Але діяльність учителя має бути націлена на учнів, які не встигають (а для сильніших учнів можна розробити комплекс додаткових вправ).
Розглянемо попередню задачу. Кінцевим результатом нашого пошуку має бути кількість годин. Як їх знайти? Задамо логічні запитання.
Яку частину басейну наповнить перша труба за 7 годину? Приймемо весь басейн за 1. Очевидно, що перша труба за 1 годину наповнить ![]() частину басейну, оскільки вона наповнює його 10 годин.
частину басейну, оскільки вона наповнює його 10 годин.
Яку частину басейну наповнить друга труба за 1 годину? Аналогічно до першого запитання друга наповнить ![]() частину басейну за 1 годину.
частину басейну за 1 годину.
Яку частину басейну наповнять дві труби за ! годину, працюючи разом? Очевидно, що потрібно додати визначені раніше частини басейну
![]()
Тобто, дві труби, працюючи разом наповнять ![]() частину басейну.
частину басейну.
За скільки годин наповнюють басейн обидві труби, працюючи разом?
![]()
Тобто, за такий час буде виконана вся робота.
Помилка 3. Пропуск етану дослідження рішення.
На етані дослідження розв'язання з'ясовуємо, чи відповідає отримана відповідь умові завдання, звертаємо увагу на правдоподібність результату. Розглядаємо, чи є інші варіанти розв’язання задачі та, що корисного можна взяти на майбутнє з розв’язку задачі. Останнє твердження дозволяє розглядати кожне завдання як ланку в загальному вмінні розв’язувати задачі, що призводить до накопичення досвіду щодо розв’язування подібних завдань. [13]
Повернемося до нашої задачі.
- Отриманий результат, 6 годин, цілком відповідає умові поставленого запитання.
- Цей результат є правдоподібним, адже дві труби наповнили басейн швидше, ніж кожна з них окремо може це зробити.
- Також, є ще один варіант розв’язування задачі. Використаємо поняття подібності.
Відрізок ОС - графік роботи першої труби, а відрізок AD - другої труби. Абсциса точки К є шуканою відповіддю.
Оскільки трикутники АКС і DKO подібні, причому OD:AC= 15:10-3:2, то й OM:BC = 3:2
Нехай ОМ = х, тоді ВС = 10-х, отже
![]()
![]()
![]()
Отже, відповідь: дві труби, працюючи разом, наповнюють басейн за 6 годин.
- Після розв’язання цієї задачі робимо висновок, що для початку всю роботу приймаємо за 1. А далі розв’язок буде залежати від поставлених запитань.[45]
Помилка 4. Змішання етапів аналізу й пошуку способів розв’язування та самого розв’язку.
Щоб уникнути змішання етапів аналізу й пошуку способів розв’язання, вчитель має знати, яку мету він переслідує на кожному етапі.
Так, мета етапу аналізу задачі – виявити всі наявні зв’язки між даними і шуканими величинами, чому допоможе складання таблиці, або схеми, або малюнка.
Мета етапу пошуку способу розв’язування – вибрати метод ( алгебраїчний чи арифметичний) і скласти план розв’язання.
Оскільки цілі етапів різні, то суміщати їх ніяк не можна. Визначимо чіткий план послідовних дій. [3]
І Іа етапі аналізу умови задачі:
- Розбиваємо умову задачі на логічні частини.
- З'ясовуємо, які величини характеризують описуваний в умові процес.
- З'ясовуємо, які величини відомі, а які потрібно знайти.
- Встановлюємо зв’язки між величинами.
На етапі пошуку розв’язку з'ясовуємо, що можна знайти за даними задачі, і чи допоможе це при подальшому розв’язуванні. Якщо для розв’язання задачі обраний алгебраїчний метод, то пошук здійснюємо за такими етапами:
- Визначаємо умови, за допомогою яких можна скласти рівняння, і вибираємо найдоцільнішу з них.
- Складаємо схему рівняння до відповідно обраної умови.
- Визначаємо, які величини можна позначити за х і обираємо найдоцільнішу.
- Визначаємо, які величини можна виразити через іншу, що позначити за х, якщо це потрібно, і обираємо найдоцільнішу.
- Завершуємо етап пошуку складанням плану виконання завдання.
Помилка 5. На етапі аналізу умови фіксуються не всі зв’язки між величинами.
Аналізуючи умову задачі, обов’язково потрібно зафіксувати всі зв’язки між даними в умові величинами. Упустивши який-небудь зв'язок, можна втратити багато інформації. Наприклад:
- Умову для складання рівняння.
- Можливість одну величину виразити через іншу.
- Можливість швидкого й очевидного розв’язання задачі.
- Передбачення кількох способів вирішення завдання.
Якщо всі вище вказані пункти учні відокремлять, то розв'язання задачі буде набагато швидшим і цікавішим.
Помилка 6. Пошук розв’язку завдання алгебраїчним методом починається з вибору змінної.
Якщо починати розв'язання задачі з вибору змінної, то можна ніколи не розв’язати цю задачу. Адже наші припущення можуть бути неправильними й остаточно заплутати розв'язання, або може бути раціональніший спосіб вибору змінної, який допоможе учням зекономити час, наприклад на контрольній роботі. Розглянемо подібну ситуацію. [7].
На уроці не були проведені етапи аналізу й пошуку розв’язку задачі. Вчитель викликає розумного учня до дошки, який знає, як розв’язати дану задачу. Очевидно, що свої записи на дошці дитина почне зі слів “Нехай х - це...”. Але, інший учень не зрозумів, чому і як вибраний х. Тому він просто перепише розв’язок і надалі навмання буде обирати, що позначати за х.
Набагато краще й ефективніше буде, коли буде проведений відповідний аналіз задачі. Учень, зможе скласти таблицю або малюнок за умовою, знайти кілька умов для складання рівняння, записати схему цього рівняння та розв’язати його. Якщо ж обрана схема з однією невідомою величиною не розв’язалася, то можна спробувати скласти рівняння з іншою величиною.
Вчителю потрібно звернути увагу на те, що при перерахуванні етапів, які ми проводимо у пошуку розв’язку задачі алгебраїчним методом, спочатку був названий вибір умови для складання рівняння, далі складання схеми рівняння, і тільки після нього вибирається змінна.
Помилка 7. Постановка запитань, які підказують учням відповідь.
На уроках математики потрібно розвивати логіку мислення. Тому недоцільно давати явні підказки учням, адже вони будуть їх чекати завжди. Потрібно налаштовувати учнів на самостійний пошук способів розв’язання, дати їм час на роздуми. Якщо ж результату немає, тоді наштовхнути дітей на правильну відповідь.
Так, замість запитань: “ Який час перебували туристи в дорозі? ”, “ Які машини знаходяться в автопарку? ”, “ У скільки турів проходить олімпіада? ”, краще ставити загальні запитання: “ Які частини можна виділити в задачі? ”,
“Що можна знайти за даними задачі? ”," Які об’єкти беруть участь у задачі?» “Що відбувається за умовою задачі?”. Постановка таких запитань може викликати нові ідеї до розв’язання. Тому всі пропозиції потрібно обов'язково вислухати, розібрати та записати найдоцільніші до зошитів. [68]
Отже, навички учнів, їх розуміння предмета та вміння використовувати отримані знання на практиці, залежить від учителя. Як педагог зуміє організувати роботу на уроці, зацікавити, пояснити, знайти підхід до дитини, так і буде проводитися урок. Текстові задачі допомагають учням розвивати уяву, логічне мислення, навчають обговорювати проблемні питання та відстоювати свої думки. Чим більше уваги вчитель буде приділяти розмові з учнями, спільним розв’язуванням, тим більше діти будуть його розуміти. А розуміння вчителя - це запорука розуміння теми уроку і математики загалом.
Виділення типових помилок та характеристика їх значення мають стати повчальними для вчителя-початківця. Для нас головне розуміння з боку дитини. Якщо учень буде вміти розв’язувати текстові задачі, це 50% ycпіху на зовнішньому незалежному оцінюванню та при вступних іспитах у деякі університети. Адже в усіх тестових контролях, тематичних підсумкових оцінюваннях обов’язково є текстові задачі. Тому, вчителі мають приділяти більше уваги саме розв’язуванню текстових задач.
- Методичні рекомендації вчителям щодо навчання учнів розв’язуванню задач
- Для кращого засвоєння особливостей математичної структури типових задач і кроків типових способів розв'язування потрібно відмовитись від змішаного порядку в розміщенні задач, споріднених за математичним змістом; розміщувані типові задачі слід компактно з різноманітними сюжетними варіаціями і ускладненнями математичного змісту, уникаючи подачі підряд великої кількості однотипних задач з метою уникнення механічного заучування способу розв’язування.
- Не давати „рецептурних” правил, особливо на початку вивчення типу задачі чи способу розв’язування, а разом із учнями створювати схеми правил- орієнтирів.
- Не потрібно намагатися поділити всі задачі на типи: потрібне доцільне поєднання розв'язування нетипових і типових задач, щоб в учнів не виникала переконаність, що за зразком без особливих зусиль розв’язуються всі задачі.
- Значну увагу слід приділяти не тільки питанням виявлення відмінностей між різними типами задач чи способами розв’язування, але й виявленню їх спільних рис;
- Під час вивчення окремого типу задачі варто подавати в певній послідовності, не ізолюючи одну від одної, а показуючи зв’язок між ними, звертаючи увагу на їх спільні та відмінні риси.
- З метою уникнення „натаскування” і розкриття різних зв’язків даного типу з нетиповими задачами та задачами інших типів доцільно організувати вивчення типових задач по наступних етапах (Додаток Л); для максимальної ефективності засвоєння учнями кожного з етапів вивчення конкретного типу необхідним с поєднання різних методів, форм і засобів навчання (зокрема і використання, відповідно до вікових особливостей учнів, дидактичних ігор та інформаційно-комунікаційних технологій).[23]
- Розміщення типових задач у курсі математики повинно бути узгоджене з вивченням теоретичного матеріалу, який стосується тих положень чи властивостей, що покладені в основу того чи іншого способу їх розв’язання.
- Доцільно навчати учнів за текстами задач створювати різного виду моделі (графічні схеми, таблиці, схематичні ілюстрації тощо) і еврисіичні схеми (правила-орієнтири) типових арифметичних способів; пропонувати завдання на формування в них умінь використовувати наявні математичні знання до вивчення різних процесів реального світу.
- Типові задачі, що розв'язуються арифметичними чи алгебраїчними способами, потрібно об'єднати в систему, яка надасть кожному учневі можливість вибору своєї власної „траєкторії руху" (порядок вивчення ускладнень типів чи способів розв'язування).
- Одним із основних результатів навчання учнів розв'язуванню текстових задач має бути поповнення наявних в учнів знань про задачу, її структурні елементи (умова і вимога), про етапи процесу розв'язування (в тому числі вивчення різних видів аналізу тексту, пошуку плану та перевірки отриманого розв'язку), тому учням слід пропонувати завдання на проведення аналізу задачі чи побудову моделей різних видів тощо.
- Задача має бути цікавою для учнів за своїм змістом і шляхом отримання відповіді та сприяти формуванню чітких уявлень про величини, що розглядаються; числові дані повинні мати пізнавальну й практичну цінність і відповідати обставинам, у яких могла виникнути потреба розв'язувати таку задачу (відповідно її постановка питання має бути реальною); корисно пропонувати задачі без готових числових даних з метою формування в учнів умінь користуватися довідниками та робити математичну обробку своїх спостережень і вимірювань.[76]
- Основним для розв'язування задач арифметичними чи алгебраїчними способами с курс математики в 5-6-х класах; у 7-9-х класах слід використовувати типові задачі для пропедевтики і введення алгебраїчного та арифметичного методів. Для показу зв’язків між різними навчальними предметами: математика і фізика ( економіка, хімія, географія тощо).
ВИСНОВКИ ДО ТРЕТЬОГО РОЗДІЛУ
В даному розділі проаналізовано практичну частину дослідження умінь учнів розв'язувати текстові задачі. Нами з’ясовано, які моменти в шкільній математиці потребують додаткової уваги (знання учнями типології текстових задач), як атмосфера уроку впливає на самооцінку учня, що є причиною любові
до математики.
Практичпо доведено, що починаючи з 7 класу, учителям потрібно приділяти більше уваги розв’язуванню текстових задач, стимулювати учнів до робот на уроці та зацікавлювати їх математикою.
Також нами розглянуті типові методичні помилки, яких вчитель допускається на уроці. З’ясування та аналіз даної проблеми дають змогу кожному учителю проаналізувати свою систему роботи та виправити всі неточності в ній. Очевидно, що виправлення помилок сприятимуть підвищенню зацікавленості учнів математикою загалом.
Опираючись на вище продемонстровані матеріали, ми даємо методичні
рекомендації вчителям, які допоможуть при навчанні дітей розв’язувати текстові задачі.
РОЗДІЛ 4
ГОРІННЯ, ЙОГО ВИДИ. УМОВИ, НЕОБХІДНІ ДЛЯ ГОРІННЯ. РІЗНОВИДНОСТІ ГОРІННЯ
Правильна організація протипожежних заходів і гасіння пожеж неможливі без чіткого розуміння сутності хімічних та фізичних процесів, які відбуваються під час горіння речовин. Тому досконале знання цих процесів дає можливість у разі необхідності швидко припиняти їх протікання та успішно боротися з вогнем.
Горіння - це екзотермічна реакція окиснення речовини, яка супроводжується виділенням диму та (або) виникненням полум'я та (або світінням.
Дим - видимі тверді та рідинні часточки в газах, утворені внаслідок горіння або піролізу матеріалів.
Полум'я - зона горіння в газовій фазі з видимим випромінюванням світла
Світіння - безполуменеве горіння матеріалу (речовини) у твердій фазі з видимим випромінюванням світла із зони горіння (наприклад, тління).
Горіння являє собою комплекс взаємопов’язаних хімічних і фізичних процесів. Основними такими процесами є: виділення значної кількості тепла; швидке хімічне перетворення горючої речовини внаслідок реакції окиснення.
Найбільш загальною властивістю горіння є властивість утвореного осередку полум'я переміщуватися по всій горючій суміші шляхом передавання тепла або дифузії активних частинок із зони горіння до свіжої суміші. У першому разі реалізується тепловий, а в другому - дифузний механізм поширення полум'я. Зазвичай, горіння протікає за комбінованим тепловим дифузним механізмом.
В основному розрізняють такі види горіння:
- за кількістю окисника: повне та неповне;
- за швидкістю поширення полум'я: дефлаграційне (від кількох сантиметрів до кількох метрів за секунду), вибухове (десятки, сотні метрів за секунду), детонаційне (тисячі метрів за секунду);
- за агрегатним станом речовин, що беруть участь у процесі горіння: гомогенне (речовини мають однаковий агрегатний стан, наприклад, горіння горючих газів на повітрі) та гетерогенне (речовини мають різний агрегатний стан і наявна межа їх розподілу, наприклад, горіння рідин і твердих речовин на повітрі). [25]
Повне горіння відбувається, якщо є достатня кількість окисника. Під час такого горіння утворюються продукти, нездатні до подальшого окислення та горіння (діоксид вуглецю, водяна пара, сірчаний ангідрид тощо). Для повного горіння горючої речовини на повітрі необхідна його відповідна кількість. Так, для повного горіння 1 кг деревини необхідно 4,18 м3 повітря, 1 кг торфу- 5,8 м3, 1 кг бензину - 10,25 м3, 1 кг пропану - 23,8 м3.
Якщо кількість окисника є недостатньою, то горіння буде неповним і реакція окиснення речовини пройде не до кінця. Під час неповного горіння утворюються, як правило, токсичні та горючі речовини (монооксид вуглецю, альдегіди, смоли, спирти тощо), які за певних умов здатні до подальшого горіння. Ознакою неповного горіння є дим. У більшості випадків на пожежах спостерігається неповне горіння речовин і як наслідок - значне виділення диму.
Треба зазначити, що під час повного горіння ефективність згорання палива є значно вищою. При неповному горінні 1 кг вугілля утворюється майже в чотири рази менше тепла, ніж при його повному горінні. Крім того, з витяжної труби опалювальної установки йде дим та іноді летить сажа.
Якщо при гомогенному горінні горюча речовина та окисник не перемішані між собою, то відбувається дифузне горіння. У цьому випадку швидкість горіння є відносно невисокою, оскільки залежить від швидкості дифузії окисника в зону горіння.
Коли окисник та горюча речовина перебувають в однаковому агрегатному стані й рівномірно перемішані між собою (наприклад, суміш горючого газу і повітря), то відбувається гомогенне кінетичне горіння. У цьому випадку швидкість горіння не залежить від дифузії повітря, а визначається швидкістю хімічної реакції і проявляється як вибух або детонація.
Пожежі, як правило, характеризуються гетерогенним дифузним горінням, швидкість переміщення полум'я якого залежить від швидкості дифузії кисню повітря до осередку горіння.
Для виникнення горіння необхідна наявність в одному місці та в один час трьох компонентів: горючої речовини, окисника та джерела запалювання (рис. 4). Крім того, потрібно, щоб горюча речовина була нагріта до необхідної температури та знаходилась у відповідному кількісному співвідношенні з окисником, а джерело запалювання мало необхідну енергію для початкового імпульсу (запалювання). Так, сірником можна запалити аркуш паперу, а дерев'яну колоду - неможливо. Необхідність для горіння одночасно трьох компонентів, так званий трикутник вогню, виявив ще в XVIII ст. французький вчений Лавуазье. [ ІЗ]
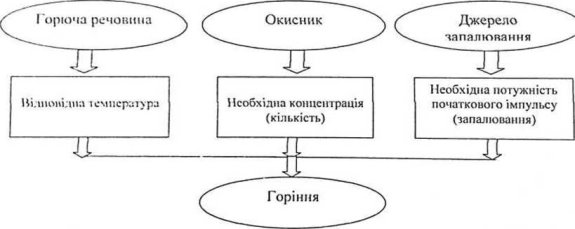
Рис. 4. Умови, необхідні для виникнення горіння
Після виникнення горіння протікає тим інтенсивніше, чим більшою є питома площа контакту горючої речовини з окисником (паперові обрізки горять інтенсивніше, ніж пачки паперу) і чим вищою є концентрація окисника, температура та тиск. На пожежах температура досягає 1000-1300 °С, а в окремих випадках, наприклад, під час горіння магнієвих сплавів - 3000 °С.
Горючими речовинами вважаються речовини, які у разі дії на них високих температур, відкритого полум'я чи іншого джерела запалювання можуть займатися і в подальшому горіти з утворенням тепла та, зазвичай, випромінюванням світла. До горючих речовин належать: дерево, папір, тканини, більшість пластмас, природний газ, бензин, гас та інші речовини в твердому, рідинному, газоподібному стані. Як правило, найбільш небезпечними у пожежному відношенні с горючі речовини в газоподібному стані.
До складу переважної більшості горючих речовин входять вуглець (Карбон) та водень (Гідроген), які є основними горючими складниками цих речовин. Тому й основними продуктами повного горіння (при достатній кількості кисню) горючих речовин є С02 та Н20. Є також ціла низка горючих речовин, які являють собою прості елементи, наприклад, сірка (Сульфур), фосфор (Фосфор), вуглець (Карбон).
Горючі речовини мають різну теплотворну здатність, тому температура на пожежах залежить не лише від кількості речовини, що горить, але й від її якості (хімічного складу). В табл. 4.4 наведено температуру полум'я під час горіння деяких речовин та матеріалів.
Окисником під час горіння речовин найчастіше виступає кисень повітря - О.,. Однак зі зменшенням вмісту кисню в повітрі уповільнюється швидкість горіння, а при вмісті кисню менше 14% (норма 21%) горіння більшості речовин стає неможливим. Крім кисню, окисниками можуть бути хімічні сполуки, до складу яких входить кисень, наприклад, селітра (KNO3), азотна кислота (HNO3), марганцевокислий калій (КМп2О4), а також окремі хімічні елементи (фтор, хлор, бром). Деякі речовини містять у своєму складі кисню стільки, що його достатньо для горіння без доступу повітря (порох, вибухівка).
Джерелом запалювання, тобто ініціатором пожежі може бути: відкрите полум'я, розжарені предмети, електричні заряди, теплові процеси хімічного, електричного та механічного походження, іскри від ударів та тертя, сонячна радіація, електромагнітні та інші випромінювання. Джерела запалювання можуть бути високо-, середньо- та малопотужними.
Розрізняють такі різновиди горіння: вибух, детонація, спалах, займання, спалахування, самозаймання, самоспалахування, тління.
Вибух - надзвичайно швидке хімічне перетворення, що супроводжується виділенням енергії й утворенням стиснених газів, здатних виконувати механічну роботу. Переважно ця механічна робота зводиться до руйнувань, які виникають під час вибуху й обумовлені утворенням ударної хвилі - раптового скачкоподібного зростання тиску. При віддаленні від місця вибуху механічна дія ударної хвилі послаблюється.
Детонація - це горіння, яке поширюється зі швидкістю кілька тисяч метрів за секунду. Виникнення детонації пояснюється стисненням, нагріванням та переміщенням незгорілої суміші перед фронтом полум'я, що призводить до прискорення поширення полум'я і виникнення в суміші ударної хвилі. Таким чином, наявність достатньо потужної ударної хвилі є необхідною передумовою для детонації, оскільки в цьому разі передача теплоти в суміші здійснюється не шляхом повільного процесу теплопровідності, а поширенням ударної хвилі.
Спалах - короткочасне інтенсивне згоряння обмеженого об'єму газоповітряної суміші над поверхнею горючої речовини або пилоповітряної суміші, що супроводжується короткочасним видимим випромінюванням, але без ударної хвилі й стійкого горіння.
Займання - початок горіння під впливом джерела запалювання.
Спалахування - займання, що супроводжується появою полум'я.
Тління - безполуменеве горіння матеріалу (речовини) у твердій фазі з видимим випромінюванням світла із зони горіння.
Самозаймання - початок горіння внаслідок самоініційованих екзотермічних процесів.
Самоспалахування - самозаймання, що супроводжується появою полум'я.
Самозаймання виникає тоді, коли внаслідок екзотермічних процесів швидкість виділення тепла в масі горючої речовини перевищує швидкість його розсіювання в навколишнє середовище. Ініціювати екзотермічні процеси, а відтак спричинити самозаймання можуть:
- висока температура горючої речовини, обумовлена дією зовнішньою джерела нагрівання (теплове самозаймання);
- життєдіяльність мікроорганізмів у масі горючої речовини, шо призводить до її самонагрівання (мікробіологічне самозаймання);
- хімічні реакції, внаслідок дії на речовину повітря, води чи хімічно активних речовин (хімічне самозаймання).
Теплове самозаймання виникає в масі матеріалів, які знаходяться в енергетично сприятливому вихідному стані для вступу в реакцію обміну з киснем повітря, під час нагрівання ззовні. Таке нагрівання може здійснюватись такими шляхами:
- контактним (унаслідок теплообміну під час контакту з нагрітим предметом);
- радіаційним (унаслідок променистого тепла);
- конвективним (унаслідок передачі тепла повітряним потоком).
До мікробіологічного самозаймання здатні органічні дисперсні та волокнисті матеріали, всередині яких можлива життєдіяльність, так званих термофільних мікроорганізмів. Саме життєдіяльність таких мікроорганізмів призводить до первинного самонагрівання маси матеріалу. Особливо схильні до мікробіологічного самозаймання невисушені речовини рослинного походження, складені в купу (сіно, солома, зерно, льон, бавовна, торф тощо). Мікробіологічне самозаймання виникає у період від 10 до 30 діб з моменту початку процесу.
Хімічне самозаймання виникає внаслідок дії на горючу речовину повітря, води чи хімічно активних речовин.
До речовин, що здатні самозайматися внаслідок дії на них кисню повітря, належать олії, жири та оліфи. Однак для цього необхідні відповідні умови. Так,
при зберіганні цих речовин у тарі самозаймання не відбувається, оскільки поверхня їх дотику з повітрям надто мала. У той же час просочені ними волокнисті матеріали мають розвинену поверхню окиснеиня, що суттєво збільшує їх здатність до самозаймання. Проте ще однією неодмінною умовою є складання просочених матеріалів у купу, штабелі, пакети. У цьому випадку поверхня окислення значно перевищує поверхню тепловіддачі, що призводить до самонагрівання речовин з подальшим їх самозайманням.
До речовин, що здатні самозайматися у разі дії на них води, належать калій, натрій, цезій, карбіди кальцію та лужних металів тощо. Ці речовини під час взаємодії з водою виділяють горючі гази, які нагріваються за рахунок теплоти реакції та самозаймаються.
До хімічно активних речовин, що можуть викликати самозаймання, належать головним чином окисники: стиснений кисень, азотна кислота, перманганат калію, перекис натрію, селітри, хлорне вапно та ін.
Наприклад, стиснений кисень призводить до самозаймання мінеральних мастил, які не займаються на повітрі. А рослинні матеріали (солома, сіно, льон, бавовна, тирса), скипидар, етиловий спирт самозаймаються в результаті контакту з азотною кислотою. [48]
Здатність самозайматися речовин та матеріалів необхідно врахувати під час розроблення заходів пожежної профілактики під час їх зберігання, транспортування, термообробки, виконання технологічних операцій тощо.
ВИСНОВКИ ДО ЧЕТВЕРТОГО РОЗДІЛУ
Правильна організація протипожежних заходів і гасіння пожеж неможливі без чіткого розуміння сутності хімічних та фізичних процесів, які відбуваються під час горіння речовин. Тому досконале знання цих процесів дає можливість у разі необхідності швидко припиняти їх протікання та успішно боротися з вогнем.
В даному розділі з'ясовано та проаналізовано причини виникнення горіння та його наслідки, види горіння та їх характеристика.
Отже, можна зробити висновок, що ознайомлення та розуміння поданого матеріалу допоможе попередити або уникнути будь яку реакцію речовини, яка буде супроводжуватися виділенням диму та виникненням полум’я.
ЗАГАЛЬНІ ВИСНОВКИ
Проблема текстових задач с актуальною для нашого суспільства. Адже тепер, ми розуміємо, яку важливу роль відіграють саме текстові задачі в житті дитини. Найпростіші життєві ситуації, в яких треба вміти обчислити якусь величину, можна вважати задачею. Такі ситуації з розвитком суспільства ускладнюються і потребують відповідного рівня математичних знань. Задачі стимулювали не лише виникнення математичної науки, а й її розвиток. Насамперед вони змушували вчених розробляти нові алгоритми, розкривати закономірності відношень у величинах, створювати нові методи дослідження, - тобто збагачувати математику новими відкриттями. Відповідно до завдань:
- нами з’ясовано, що суть текстової задачі полягає в тому, що у найширшому плані вона передбачає необхідність свідомого пошуку відповідних засобів для досягнення мети, яку добре видно, але яка безпосередньо недосяжна, а у психологічному аспекті задача розглядається як свідома мета, що існує в певних умовах, а дії - як процес, спрямовані на досягнення мети. Класифікують текстові задачі по характеру об’єктів та по відношенню до теорії. Також, нами з’ясовано, що основними способами розв’язування текстових задач є аналітичний та синтетичний;
- нами представлені основні способи розв’язування різних типів текстових задач. З’ясовано, що основними способами розв’язування текстових задач є аналітичний та синтетичний. Також, на прикладах, запропоновано використання диференційованого навчання розв’язуванню текстових задач та проаналізовано методику навчання розв’язанню текстових задач в закордонних школах. На завершення, нами було з’ясовано особливості навчання розв’язуванню текстових задач в закордонних школах. Аналіз закордонної методики значно допомагає розширенню уявлення про методику розв’язування текстових задач та уникненню незрозумілостей з боку дитини;
- нами досліджено стан готовності учнів розв’язувати задачі. Можна зробити висновок, що дітям подобається розв’язувати задачі лише в тому випадку, коди вони є цікавими та логічними. Визначено критерії за якими учні визначають улюблений предмет та виділено типові методичні помилки вчителя при розв'язуванні текстових задач;
- нами були розроблені та запропоновані методичні рекомендації вчителям, щодо навчання учнів розв’язуванню текстових задач. На мою думку, основою у процесі розв’язування текстових задач майже завжди с малюнок. Наочне зображення умови задачі у вигляді схеми чи малюнка полегшує процес міркувань. При розв’язуванні задачі не допускаються необгрунтовані узагальнення, аналогії, ставиться вимога повноти диз’юнкції, повноти витриманності класифікації.
У четвертому розділі ми висвітлили питання безпеки життєдіяльності, а саме горіння, причини його виникнення та можливі наслідки.
Я вважаю, що майбутньому вчителю слід пам’ятати, що крім формування суто математичних знань текстові задачі розвивають пізнавальну активність, ерудицію учня, вчать його чіткості, лаконічності викладу думок, обґрунтуванню правильності власних міркувань, застосуванню символіки тощо.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
- Балл Г.А. Базовые понятия теории задач./ Балл Г.А. И К.: Изд. Института кибернетики АН УССР, 1978.-216 с.
- Бевз Г.П. Методика викладання математики / Бевз Г.П. // Навч.посібник. - 3- тє вид., перероб. і допов. - К.: Вища шк.., 1989. - 367 с.
- Білий І.П. Задачі для розвитку логічного мислення школярів молодшого і середнього віку. / Білий І.П. // Математика в школах України. - 2008, - № 14- І5.-С.23
- Богданович М.В. Методика розв’язування задач у початковій школі. /
Богданович М.В.// К.: Вища школа, 1990.-182 с.
- Богоявленский Д.Н. Психология усвоения знаний в школе. І Богоявленский
Д.Н, Менчинская Н.А. //М.: Изд-во А.П.Н. РСФСР. 1959. - 347с.
- Болтянський В.Г. Использование логической символики при работе с
определениями / Болтянський В.Г. // Математика в школе. - 1973. - № 5. - с. 45-50.
- Брунер Дж. Исследование развития познавательной деятельности: Пер. с
англ. М.: Педагогика, 1972,391 с.
- Брунер Дж. Процес обучения: Пер. с англ. М.:Изд-во А.П.Н. РСФСР, 1962. -
84 с.
- Брунер Дж. Психология познания/ Пер. с англ. М.:Прогресс, 1977. - 412 с.
- Війчук Г.В. Розвиток в учнів здібностей спостерігати та аналізувати у
процесі вивчення математики І Війчук Г.В., Війчук Т.І. //Сучасний стан і перспективи шкільних курсів математики та інформатики у зв'язку з реформуванням у галузі освіти: тези доповідей, Дрогобич, 2000. - С.116- 118.
- Возняк Г.М., Маланюк К.П. Прикладна спрямованість шкільного курсу
математики. / Возняк Г.М., Маланюк К.П. //- К.: Рад. шк., 1984. - 80 с.
- Галайко М.Є. Розвязування задач па відсотки. Урок математики в 6 класі. /
Галайко М.Є. // Математика в школах України. - 2009, -№34. - С.21
- Гамезо М.В. Возрастная и педагогическая психология: Учебное пособие для
студентов пед.ин-тов по специальности «Педагогика и методика начального обучения» /М.В.Матюхина, Т.С.Михальчик, Н.Ф.Прокина, Л од. рсд. М.В. Гамезо и др. //- М.: Просвещение, 1984.-256 с.
- Гарнагіна І.А. Як навчити розв’язувати задачі / Гарнагіна I.А. // Математика в школах України.- 2008, - № 27. - С.7
- Глібова А.В. Текстові задачі з математики. 5-6 клас. / Глібова А.В. // Математика в школах України. - 2006, -№27.- С.31
- Груденов Я.И. Психолого-дидактические основы методики обучения математике. - М.: Педагогика, 1987. - 160 с.
- Гудименко Ф.С. Російсько-український математичний словник. / Гудименко Ф.С., Погребиський Й.Б., Сакович Г.Н., Чайковський М.А. И Харків: Основа, 1990.
- Давыдов В.В. Виды обобщений в обучении. М.: Педагогика, 1982.- 423с.
- Давыдов В.В. Проблемы развивающего обучения: Опыт теоретического и
экспериментального психологического исследования. - М.: Педагогика, 1986.-240 с.
- Коваленко В.Г. Дидактические игры на уроках математики.
М..Просвещение, 1990.-96 с.
- Коваленко В.Г., Слсдзінський 1.Ф. Математична символіка. К., 1981.- 80с.
- Коломісць А.М. Формування культури логічного мислення вчителя у
процесі навчання математики / Коломісць А.М. //Придніпровський науковий вісник. - №.’130(197) ,1998. - С.51-56.
- Колягин Ю.М. Методика преподавания математики в средней школе. Общая методика / Колягин Ю.М., Оганесян В.А., Саннинский В.Я., Луканкин Г.Л. // Учеб, пособие. - М.: Просвещение, 1975. - 280 с.
- Коцюк І.М. Текстова задача з математики як засіб засвоєння економічних понять учнів початкових класів освіти / Коцюк І.М. //Наукові записки Тернопільського національного педагогічного університету. Серія: Педагогіка. - 2005. - №2. - С.85-87.
- Крикунов ГЛ. Безопасность жизнедеятельности. / Крикунов ГЛ., Беликов АС., Залупив В. Ф. И Днепропетровск: Пороги, 1992. — 4.1. — 412с.
- Крутецкий В.А. Психология обучения и воспитания школьников. Книга для учителей и классных руководителей. М., „Просвещение”, 1976. - 303 с.
- Кухар В.М. Математика. Множини, логіка, цілі числа. Практикум. / Кухар
В.М., Тадіян С.І., Тадіян В.П. // К.: Вища школа, 1989. - 332 с.
- Кушнір В.А. Системний аналіз педагогічного процесу: методологічний
аспект [Монографія]. - Кіровоград: Видавничий центр КДПУ, 2001. - 348 с.
- Лабораторные и практические работы по методике преподавания
математики: Учеб, пособие для студентов физ.мат. спец. пед. ин-тов /Е.И.Лященко, К.В.Зобкова, Т.Ф.Кириченко и др.; Под ред. Е.И.Лященко. - М.: Просвещение, 1988. -223 с.
- Лаврова Н.Н. Задачник-практикум по математике./ Лаврова И.11., Стойлова
Л.П. И М., Просвещение. - 1985. - 183 с.
- Левин А.Н., Смирнова В.В, О необходимости решения типовых задач// Математика в школе. -1963. - №1. -С.58
- Литвиненко В.Н. Практикум по элементарной математике. / Литвиненко
В.Н., Мордкович А.Г. // М.: Просвещение, 1991. -352 с.
- Лодатко Є.О. Математична культура як феномен сучасного інформаційного
суспільства І Лодатко Є.О. //Рідна школа /Щомісячний науково- педагогічний журнал. - 2004, №9(896). - С.24-27.
- Любохинець Л.С. Вплив інформаційного суспільства на розвиток
інтелектуального потенціалу України / Любохинець Л.С., Бабич Л.М. //Актуальні проблеми входження вищих навчальних закладів України до єдиного європейського освітнього простору: Матеріали міжнар.наук.- метод.конф. - К.: Київський національний торгівельно-економічний ун-т, 2005. – С.72-74.
- Макара В.Л. Виховання професійної культури особистосі і методами
природничо-математичних дисциплін І Макара В.Л., Коломісці. А.М. //Морально-духовний розвиток особистості в сучасних умовах /36.наук, праць. - Київ, 2000. - С.266-270.
- Максимович О.М. Розвиток логічного мислення школярів — одне з важливих завдань шкільного курсу математики / Максимович О.М. //Сучасний стан і перспективи шкільних курсів математики та інформатики у зв'язку з реформуванням у галузі освіти: тези доповідей, Дрогобич, 2000. - С.77-79.
- Малафіїк О.1. Про організаційно-педагогічні заходи з розвитку уяви та
образного мислення у школярів на комп’ютерній основі /Малафіїк О.І. //Оновлення змісту, форм та методів навчання і виховання в закладах освіти: Зб.наук.праць Наукові записки Рівненського державного гуманітарного університету. Випуск 23. - Рівне.РДГУ, 2002. - С.60-6І.
- Математика в понятиях, определениях и терминах: В 2-х ч.: 4.2/
О.В.Мантуров, Ю.К.Солнцев, Ю.И.Соркин, Н.Г.Федин. - К.: Рад.шк., 1986. – 360 с.
- Методика викладання математики в середній школі: Пер.з рос. /О.Я.Блох,
Е.С.Канін, Н.Г.Килина та ін.; Упоряд. Р.С.Черкасов, А.А.Столяр. - X.: Вид- во “Освіта” при Харк. Ун-ті, 1992. - 304 с.
- Миценко І.М. Забезпечення життєдіяльності людини в навколишньому
середовищі. / Миценко С.В.// — Кіровоград, 1998. — 292 с.
- Мухина В.С. Возрастная психология: Учебник. / Мухина В.С.// - М.:
«Академия», 1999. - 198 с.
- Пастернак 0.1. Задачі на змішування в курсі алгебри основної школи /
Пастернак 0.1. // Математика в школах України. - 2005, -№5 - С.16
- Петухова Л.І. Про рішення текстових завдань з математики/ Петухова
Д.1. / / Фестиваль педагогічних ідей «Відкритий урок». - М.: Перше вересня
- Розентуллер Р.М. Составление и решение комплексных задач \ Розентуллер Р.М.//Математика в школе. - 1972,-№1 — С.32
- Сисоєнко Н.А. Використання поняття подібності дня формування навичок розв’язувати задачі на спільну роботу / Сисоєнко Н.А., Сисоєнко В.М. // Математика в школах України, 2010, № 32. - С. 13-17.
- Скафа Е.И. Эвристическое обучение математике как методическая епеїема
лнчностно-развнваюшего образования / Скафа Е.И.//Віспик Черкаського університету. Серія: педагогічні науки, 2005. — Випуск 72. С.4І 46.
- Скобко Ю.С. Безпека життєдіяльності / Скобло Ю.С., Тіщснко Л.М., Цапко
В.Г. //— Вінниця: Нова книга, 2000. — 368 с.
- Скоробогатов В.А. Феномен воображения: Философия для педагогики и
психологии. I Скоробогатов В.А., Коновалова Л.И. И учебное пособие. — СПб.: Изд-во «Союз», 2002. - 1S3 с.
- Слєпкань 3.1.Методика навчання математики: Підручник. - 2-ге вид., допов.і
нереробл. - К.: Виша шк.., 2006. - 582 с.
- Сологуб А.1. Концепція креативної природничо-наукової освіти І Сологуб
А.1. /Рідна школа. - Хе 12,2000. - С. 15-34.
- Сологуб А.І. Принципові відмінності креативної природничонаукової освіти
/ Сологуб А.1. //Неперервна професійна освіта: теорія і практика: Збірник наукових праць /За редакцією І.А.Зязюна та Н.Г.Ничкало. - У двох частинах. - 4.2. - К., 2001. - 302 с.
- Сохор А.М. Логическая структура учебного материала. Вопросы
дидактического анализа. - М.: Педагогика, 1974.
- Стеценко А. Методика розв’язування простих текстових задач І Стеценко А.,
Степаненко Т. // Дефектолог, 2011, Х"5. - С. 55-57
- Танник Н.А. Задачі на розчини і сплави. 9 клас. І Танник Н.А. // Математика
в школах України. - 2008, - Х°6. - С.26
- Тарасенкова Н.А. Семіотичний підхід до математичної освіти / Тарасенко
11-А. // Збірник наукових праць. Педагогічні науки. Випуск 37. - Херсон: Видавництво ХДУ, 2004. - С. 129-133
56. Тарасов В.. Ніздрай Л. Інноваційні підходи у внкаадаипі курсу методики математики \ Тарасов В. \\ Школа першого ступеня: теорія і практика: Зб.наук.пр. Переяслав-Хмельницького державного педагогічного університету імені Григорія Сковороди. - Випуск 7. Переяслав- Хмельнпцький, 2003. - С. 169-175.
- Федченко Л.Я. Узагальнення і систематизація знань при вивченні шкільного
курсу математики / Федченко Л.Я. //Сучасний стан і перспективи шкільних курсів математики та інформатики у зв'язку з реформуванням у галузі освіти: тези доповідей, Дрогобич, 2000. - С.80-82.
- Философский словарь /Под ред. И.Т.Фролова. - М.: Политииздат, 1987.
- Финкельштейн В.М. Заинтересованность учеников / Финкельштейн В.М. //
Математика в школе. - 1993. - № 2. - с. 17-21.
- Фомичев В.А., Фомичева О.С. Новые теория и методы раннего позитивного
развития интеллекта детей в информационном обществе vdrfom@aha.ru, vladfom@yahoo.com
- Фридман Л. М. Педагогический опыт глазами психолога. — М.:
Просвещение, 1987.
- Фридман Л. М. Урок? Нет, тема (технология педагогического труда) / Фридман Л.М. // Народное образование. - 1990.- № 1.
- Фридман Л.М. Логико-психологический анализ школьных учебных задач.
М.: Просвещение, 1977.-207 с.
- Фридман Л.М. Наглядность и моделирование в обучении. - М.: Знание, 1984.
-80 с.
- Фридман Л.М. Психолого-педагогические основы обучения математике в
школе: Учителю математики о педагогической, психологии. - М.: Просвещение, 1983. - 160 с.
- Фридман Л.М. Учитесь учиться математике: Книга для учащихся. - М.:
Просвещение, 1985. - 112 с.
- Фройденталь Г. Математика как педагогическая задача / Фройденталь Г.//
Ч.І. Пособие для учителей/Под. ред. Н.Л.Виленкина., Сок.пер.с нем. А.Я.Халамайзера. - М.:Просвещение, 1982. - 208 с.
- Хазанкіш Р.Г. Десяті, заповедей учителя математики / Хатанкип Р.Г. //
Народное образование, - 1991.- № 1.
- Чаплигін В.Ф. Деякі методичні міркування за рішенням текстових завдань /
Чаплигін В.Ф. І Чаплигін В.Ф. 11 Математика в школі. - 2000. -№ 4. - С.28-29
- Чашечникова О.С. Дифференцированное обучение математике в контексте личностно развивающего образования / Чашсчкова О.С. // Вісник Черкаського університету. Серія: педагогічні науки, 2005. - Випуск 72. - С. 126-132.
- Черних Л.О. До проблеми удосконалення методичної підготовки майбутніх учителів математики / Черних Л.О. Н Сучасний стан і перспективи шкільних курсів математики та інформатики у зв’язку з реформуванням у галузі освіти: Тези доповідей всеукраїнської науково-практичної конференції. - Дрогобич, 2000. - С.215-217.
- Шардаков М.Н. Мышление школьника. -М., 1993. - 160 с.
- Шеварев П. А. О роли ассоциаций в процессе мышления / Шеварев П.А. //
Исследования мышления в советской психологии. —М.: Наука, 1966. — С. 47-54.
- Шкільний тест розумового розвитку. Практична психологія - школі.
Упорядники: Слободянюк І.А., Холодова О.О. Олексенко О.О. Вінниця, 1995,- 39с.
- Щербина Т.М. Професія шукає математика. Проект “Методи розв’язання текстових задач з алгебри в 9 класі” / Щербина Т.М. // Математика в шкодах України. -2008, - №13. - С.18
- Эльконин Б.Д. Кризис и основания детского развития / Эльконин Б.Д. //Вопросы психологии. - 1992. - №3-4. - С.7-13.
- Эрдниев П.М., Эрдниев Б.П. Укрупнение дидактических единиц в обучении
математике: Кн.для учителя. - М.: Просвещение, 1986.-255 с.
- Davis, Robert В. Discovery in mathematics. A text for teachers. California-London, 1964.
- Goals for School Mathematics. The Report of the Cambridge Conference on
School Mathematics. Boston, 1963.
- Suppes, Patrick. Sets anil Numbers. BooklA. N. Y., 1962.
- The Revolution in School Mathematics. Л Challenge lor Administrators and
- Teachers. Washington, 1963.
ДОДАТКИ
Додаток А
Задачі на рух
1.Спостерігач помітив, що через 14 с після того, як з’явилась блискавка, почувся удар грому. Визначити, на якій віддалі від спостерігача була гроза, коли відомо, що швидкість звуку 330 м за секунду. (4 км620 м).
2. З двох міст одночасно назустріч один одному виїхали велосипедист і мотоцикліст. Через 3 години вони зустрілися. Швидкість велосипедиста 12 км за годину, а мотоцикліста 50 км/год. Яка відстань між містами?
3. Із двох міст одночасно назустріч один одному виїхали два автобуси і зустрілися через 2 години. Швидкість першого автобуса 60 км/год., а другого - 70 км/год. Яка відстань між містами?
4. З Києва до Жмеринки вийшов швидкий поїзд і одночасно назустріч йому з Жмеринки вийшов пасажирський поїзд. Швидкість пасажирського поїзда - 65 км/год., а швидкого - 85 км/год. Через 2 години вони зустрілися. Яка відстань між містами?
5. Із двох населених пунктів, відстань між якими 90 км, виїхали одночасно назустріч один одному два велосипедисти. Перший з них рухався зі швидкістю 14 км/год., а другий - 16 км/год. Через скільки годин велосипедисти зустрінуться?
6. Із двох міст, відстань між якими 48 км, виїхали одночасно назустріч один одному два велосипедисти. Вони зустрілися через 2 години. Швидкість одного велосипедиста 14 км/год. Знайти швидкість другого.
7. Вершник проїхав відстань між двома містами за 4 години. За скільки годин проїде більшу у 8 разів відстань вантажний автомобіль, якщо його швидкість у 4 рази більша, ніж швидкість вершника?
8. З пункту О виїхав трактор з швидкістю 15 км/год. Через 4 години з цього самого пункту в протилежному напрямі виїхав бензовоз з швидкістю 45 км\год. Через скільки годин після виходу бензовоза відстань між ним і трактором становитиме 180 км?
9. З пристані одночасно в протилежних напрямах вийшли два моторних човни. Через 6 годин відстань між ними була 378 км. Знайдіть швидкість другого човна, якщо швидкість першого 35 км/год.
10. Швидкісіь теплохода у стоячій воді 25 км/год. Швидкість течії річки 5 км/год. Скільки кілометрів пройде теплохід за течією річки за 6 годин? Скільки кілометрів за цей час він пройде проти течії?
11. Два велосипедисти виїхали назустріч один одному з двох міст, відстань між якими 180 км. Яка відстань буде між велосипедистами після того, як один проїхав ![]() , а другий -
, а другий - ![]() усієї відстані?
усієї відстані?
12. Відстань між містами А і В 900 км. З міста А в місто В вирушили ватажна машина і одночасно назустріч їй з міста В вирушила легкова машина. Всю відстань вантажна машина пройшла за 15 годин, а легкова - за 10 годин. Через скільки годин після виїзду машини зустрілися? (Вважати, що кожна з машин їхала рівномірно, з сталою швидкістю).
13. Відстань від А до В 7 км, а від В до С у 5 раз більша. За скільки годин велосипедист може проїхати відстань від А до С із швидкістю 14 км/год.?
14. Школярі вирушили в похід. Спочатку вони їхали 2 години поїздом із швидкістю 60 км/год., потім 3 години йшли пішки із швидкістю 4 км/год. Чому дорівнює весь шлях, який подолали учні? Яка середня швидкість пересування учнів?
15. Разом з першим автомобілем з міста А вилітає муха, швидкість якої 45 км за годину. Муха випереджає перший автомобіль, летить до другого. Зустрівши його, повертається назад до першого, зустрівши його, повертається назад до другого. Далі зустрівши другого повертається назад до першого і так продовжує літати аж до зустрічі автомобілів. Скільки км пролетіла муха. (90 км).
16. Мотоцикліст проїхав до місця призначення 370 км, зробивши одну зупинку. До зупинки він був у дорозі З години і їхав із швидкістю 70 км/год,, а після зупинки проїхав решту шляху за 2 години. З якою швидкісно їхав мотоцикліст після зупинки?
17. Геологи проїхали 420 км. Спочатку вони їхали З години на машинах із швидкістю 60 км/год., а решту часу кіньми із швидкісно 8 км/год. Скільки часу геологи їхали кіньми?
18. Катер пройшов відстань 96 км із швидкісно 24 км/год. Повертаючись назад, він витратив часу на 1 годину менше. Скільки часу витратив катер, щоб повернутися назад?
19. Літак може пролетіти без заправляння 8 000 км. Чи може цей літак, рухаючись із швидкістю 950 км/год., бути в польоті без заправляння 8 годин? 9 годин?
20. Машина вийшла з радгоспу о 13 годині і прибула в місто о 17 годині. За цей час вона пройшла 200 км. З якою швидкістю йшла машина?
21. Велосипедистові треба проїхати 34 км. Він уже проїхав 2 години з швидкістю 14 км/год. Яку відстань йому залишилося проїхати?
22. Два міста А і В знаходяться на відстані 140 км одне від одного. З цих міст одночасно назустріч один одному виїжджають два автомобілі. Перший автомобіль має швидкість 30 км за годину, а другий 40 км за годину.
Додаток Б
Задачі на зустрічний рух
- Відстань між двома містами 250 км. З цих міст назустріч один одному одночасно виїхали 2 автобуси. Яка відстань буде між автобусами; коли перший з них проїде 127 км, а другий — 93 км?
Складіть графічну схему умови задачі.
- З пристані "Київ" до пристані "Кременчук" вирушив теплохід і одночасно йому назустріч з пристані "Кременчук" вирушив катер. Теплохід йшов зі швидкістю ЗО км/год, а катер — 24 км/год. Через 5 год вони зустрілися. Яка відстань між пристанями?
Складіть графічну схему умови задачі і розв'яжіть її за діями двома способами.
- З Харкова до Запоріжжя виїхав мотоцикл і одночасно назустріч йому із Запоріжжя виїхав моторолер. Швидкість мотоцикла 55 км/год, а моторолера — ЗО км/год. Через 3 год вони зустрілися. Яка відстань між містами?
Розв'яжіть задачу, склавши числовий вираз.
- З двох залізничних станцій, відстань між якими 910 км, одночасно вирушили назустріч один одному два електропоїзди і зустрілися через 5 год. Швидкість першого електропоїзда 87 км/год. Яка швидкість другого електропоїзда?
Складіть: графічну схему умови задачі, числовий вираз розв’язання; задачу, обернену до даної, у якій треба дізнатися, через скільки годин відбудеться зустріч.
- Із села до міста, відстань між якими 48 км, виїхав велосипедист і одночасно назустріч йому з міста виїхав гусеничний трактор. Швидкість велосипедиста 14 км/год, а трактора — 10 км/год. Через скільки годин вони зустрінуться?
Розв'яжіть задачу, склавши числовий вираз.
- Відстань між містами А і В 900 км. З міста А в місто В вирушив вантажний автомобіль і одночасно назустріч йому з міста В вирушив легковий автомобіль. Усю відстань вантажний автомобіль пройшов за 15 год, а легковий – за 10 год. Через скільки годин після виїзду автомобілі зустрілися?
- З пункту А до пункту В вийшов турист зі швидкісно 4 км/год, а через 1 год 30 хв йому назустріч з пункту В вийшов другий турист зі швидкістю 3 км/год. Через 2 год вони зустрілися. Яка відстань, між пунктами А і В? Складіть графічну схему умови задачі та розв’яжіть її за діями і склавши числовий вираз.
- Відстань між пунктами А і В ЗО км. З пунктів А і В одночасно назустріч один одному вийшли два туристи. Через 2 год відстань між ними становила 12 км. Турист, що йшов з пункту В, зупинився і почав чекати першого туриста, який дістався до нього через 3 год. Які швидкості туристів?
- Відстань між пунктами А і В 36 км. З пунктів А і В одночасно назустріч один одному вийшли два туристи. Через деякий час відстань між ними становила 18 км, а ще через 2 год вони зустрілися. Відомо, що швидкість одного з туристів більша, ніж швидкість другого, на 1 км/год.
- З двох пунктів одночасно назустріч один одному виїхали два велосипедиста. Швидкість одного з них 15 км/год, а швидкість другого 13 км/год. Через скільки годин велосипедисти зустрінуться, якщо відстань між пунктами 84 км?
- З протилежних берегів ставка одночасно відпливли назустріч один одному два плавці. Перший плив зі швидкістю 40 м/хв, другий — 60 м/хв. Між плавцями весь час курсує моторний човен: від першого до другого і назад і т.д. Швидкість човна — 24 км/год. Яку відстань пройшов човен до моменту зустрічі плавців, якщо відстань між берегами ставка в цьому місці дорівнює 600 м?
- Два потяги їдуть назустріч один одному. Швидкість одного з них 65 км/год, а другого 75 км/год. Через скільки годин потяги зустрінуться, якщо зараз між ними 420 км?
- Відстань між двома пунктами 315 км. Із цих пунктів одночасно назустріч один одному вийшли дві автомашини. Швидкість однієї 50 км/год, а швидкість другої 55 км/год. Через скільки годин автомашини зустрінуться?
- Відстань між двома пристанями 525 км. Від цих пристаней одночасно назустріч один одному вийшли два катери. Швидкість одного катера 35 км/ч, а швидкість іншого 40 км ч. Через скільки часів катери зустрінуться?
- Два потяги йдуть назустріч один одному. Швидкість одного з них 65 кмюд. а швидкість іншого на ЗО км\год більша. Через скільки годин потяги зустрінуться, якщо зараз між ними 640 км?
Додаток В
Задачі на рух у протилежних напрямах
- З пункту А одночасно в протилежних напрямах виїхали колісний і гусеничний трактори. Швидкість колісного трактора ЗО км/год» а гусеничного — 10 км/год. На скільки віддаляються трактори один від одного за І год? Через скільки годин відстань між тракторами буде 120км?
- З пункту А одночасно у протилежних напрямах виїхали два автомобілі. Через 4 год відстань між ними становила 440 км. Яка швидкість автомобілів, якщо швидкість одного з них на 10 км/год менша за швидкість другого? , Використайте предметну схему.
- З пункту А виїхав велосипедист зі швидкістю 14 км/год. Через 2 год з цього ж пункту у протилежному напрямку виїхав вантажний автомобіль, швидкістю 58 км/год. Через скільки годин після виходу автомобіля відстань між ним і велосипедистом становитиме 244 км?
- З пункту А одночасно у протилежних напрямах виїхали 2 автомобілі. Перший автомобіль їхав зі швидкістю 60 км/год. Через 2 год, коли відстань між ними була 260 км, другий автомобіль зупинився на 1 год, а перший продовжував рух. Через який час від початку руху автомобілів відстань між ними становитиме 710 км?
- З одного аеродрому у протилежних напрямах одночасно вилети літаки. Швидкість першого була на 165 км/год більша, ніж швидкість друг. Через деякий час перший з них пролетів 1425 км, а другий — 1920 км. швидкості літаків?
Додаток Г
Задачі на рух в одному напрямку
- По шосе зі швидкістю 14 км/год їде велосипедист, а вслід йому зі швидкістю 50 км/год іде мотоцикліст. Через який час моїоцикліст наздожене велосипедиста, якщо відстань між ними 108 км? Яку відстань за цей час проїде мотоцикліст? Па скільки більше кілометрів за цей час проїде мотоцикліст, ніж велосипедист?
- Електропоїзд вийшов зі станції зі швидкістю 60 км/год. Через 2 год з тієї ж станції в тому самому напрямку вийшов другий електропоїзд. З якою швидкістю він має йти, щоб наздогнати перший електропоїзд за 6 год?
- Два велосипедисти виїхали одночасно з міста А в місто В, відстань між якими 120 км. Перший велосипедист першу половину шляху їхав зі швидкісно 12 км/год, а другий — 10 км/год. Другий велосипедист увесь час їхав зі швидкістю 11 км/год. Хто з них раніше приїхав до міста В ?
- Лисиця помітила зайця, коли той був на відстані 600 м від неї. Зайцю до місця, де він міг би сховатися від лисиці, бігти 2 км 160 м. Чи впіймає лисиця зайця, якщо бігтиме зі швидкістю 870 м/хв? (Швидкість зайця — 720 м/хв).
- Петрик почав наздоганяти Олега, коли той був від нього на відстані 960 м, і наздогнав його через 8 хв. Швидкість Олега у 2 рази менша, ніж швидкість Пегрика. Яка швидкість Петрика?
- З пункту А в пункт В, відстань між якими 160 км, одночасно виїжджають 2 мотоциклісти. Швидкість першого 40 км/год і він дістається до пункту В на 1 год раніше, ніж другий мотоцикліст. Яка швидкість другого мотоцикліста?
- Відстань між містами А і В 150 км. З міста А до міста В одночасно виїжджають 2 автомобілі. Швидкість першого автомобіля на 10 км/год більша, ніж швидкість другого, і він дістається до міста В за 3 год. На якій відстані від міста А у цей час знаходиться другий автомобіль?
- Від однієї пристані вирушили в одному напрямку, катер і буксир. Швидкість катера 27 км/год, а буксира — 18 км/год. Яка відстань буде між ними через З год?
- З села виїхав віз зі швидкістю 7 км/год. Коли він проїхав 20 км, вслід за ним з села виїхав вершник зі швидкістю 12 км/год. Через який час вершник наздожене віз і на якій відстані від села?
- Два велосипедисти виїхали одночасно з міста до спортивного табору. Перший їхав зі швидкістю 10 км/год, а другий — 13 км/год. Через 2 год другий велосипедист проколов камеру, тому далі йшов пішки зі швидкістю 4 км/год. На якій відстані від міста перший велосипедист наздожене другого?
Додаток Д
Задачі на знаходження середньої швидкості
- Велосипедист перші 6 год їхав зі швидкістю 14 км/год, а останні 6 год — 10 км/год. Яка середня швидкість руху велосипедиста?
- Велосипедист першу половину шляху проїхав зі швидкістю 15 км/год, а другу — 10 км/год. Яка середня швидкість руху велосипедиста, якщо довжина шляху складає 300 км?
- Велосипедист проїхав 60 км. З год він їхав до обіду зі швидкістю 14 км/год і 2 год він їхав після обіду. З якою швидкістю їхав велосипедист після обіду і яка була його середня швидкість на всьому шляху?
- Два велосипедисти виїхали одночасно з міста А до міста В, відстань між якими 120 км. Перший велосипедист першу половину шляху їхав зі швидкістю 12 км/год, а другу — 10 км/год. Другий велосипедист увесь час їхав зі швидкістю 11 км/год. Хто з них раніше приїхав до міста В ? Знайдіть середню швидкість першого велосипедиста.
- Відстань між двома містами 300 км. Автомобіль пройшов її в одному напрямку зі швидкістю 50 км/год, а у зворотному — 75 км/год. З якою середньою швидкістю рухався автомобіль?
- Відстань між містом і селом 36 км. З міста в село кінь біг зі швидкістю 12 км/год. Назад він повертався з вантажем зі швидкістю 6 км/год. Яка середня швидкість руху коня?
- Велосипедист їхав 3 год зі швидкістю 14 км/год і 2 год зі швидкістю 18 км/год. Знайти середню швидкість велосипедиста за весь час руху.
- Турист йшов пішки зі швидкістю 5 км/год і 2 год їхав на машині зі швидкістю 45 км/год. Знайти середню швидкість туриста на всьому шляху.
- Поїзд 2 год йшов із швидкістю 80 км/год і 3 год із швидкістю 90 км/год. Знайдіть середню швидкість поїзда на всім шляху.
Додаток Е
Задачі на рух за течією чи проти течії
- Теплохід їде річкою проти течії. За кожну годину він долає 16 км. Яка швидкість течії річки і яка власна швидкість руху теплохода, якщо за течією теплохід рухається зі швидкістю 20 км/год?
- Відомо, що швидкість теплохода за течією річки на 6 км/год більша, ніж швидкість його проти течії. Яку відстань пройде теплохід за течією за 3 год, якщо його власна швидкість у 6 разів більша, ніж швидкість течії?
- За течією моторний човен пройшов й км за 4 год. Цю саму відстань проти течії він пройшов за 6 год. На скільки швидкість човна за течією більша, ніж швидкість його проти течії?
- Моторний човен пройшов проти течії річки 16 км за 2 год і повернувся назад за 1 год 20 хв. Яка швидкість течії і яка власна швидкість човна?
- Вниз по річці турист проплив 12 км на плоту, а повернувся на човні. Увесь час склав 10 годин. На плоту турист плив на 2 год більше, ніж на човні. Яка швидкість течії і яка власна швидкість човна?
- Від пристані А одночасно у протилежних напрямах по річці вирушають пліт, що йде вниз за течією, і моторний човен, що йде проти течії. Швидкість течії 3 км/год, а власна швидкість моторного човна 12 км/год. Яка відстань буде між плотом і човном через 5 годин? На якій відстані від пристані А знаходитимуться окремо човен і пліт через 5 годин? Через скільки годин відстань між плотом і моторним човном становитиме 84 км?
- Відстань між пристанями А і В — 90 км. Від пристані А вниз за течією у напрямку до пристані В спускається пліт. Одночасно назустріч плоту з пристані В вирушає катер. Швидкість течії 3 км/год, швидкість катера у стоячій воді — 15 км/год. Яка відстань буде між катером і плотом через 2 год? Через який час відбудеться зустріч катера з плотом? На якій відстані від пристані В буде пліт через 2 год? На якій відстані від пристані А буде катер через 2 год?
- Мандрівник плив на плоту 3 доби. Швидкість течії річки 2 км\год. Далі мандрівник сів у моторний човен і проплив вниз за течією за 6 год відстань, що у 2 рази більша, ніж попередня. Яка власна швидкість човна?
- Буксир йде проти течії річки і долає відстань в 285 км. між двома портами за 19 год. Скільки часу потрібно буксиру, щоб повернутися назад, якщо швидкість течії 2 км\год?
Додаток Є
Варіанти задач на рух підвищеної складності
- Два теплоходи вийшли о 7 годині назустріч один одному і зустрілися о 23 годині того ж дня. Один з них мав швидкість 24 км/год і зупинявся на І год. Яка швидкість другого теплохода, якщо спочатку відстань між теплоходами була 936 км?
- О 6 год з пункту А до пункту В виїхав велосипедист, а через 2 год назустріч йому з пункту В виїхав автомобіль. Вже після зустрічі, о і 2 год, відстань між ними становила 72 км. О якій годині вони зустрілися, якщо відстань між А і В 240 км, а швидкість автомобіля у 5 разів більша за швидкість велосипедиста?
- З пункту А виїхав автобус і через 12 хв наздог нав пішохода, що вийшов з пункту В одночасно з виїздом автобуса і в чому ж напрямку. Швидкість автобуса 40 км/год, а пішохода — 5 км/год. Яка відстань між пунктами А і В1
- Швидкість течії річки 5 км/год. Тещохід пройшов вниз за течією 240 км за 8 год. Скільки часу він буде повертатися назад, маючи ту ж саму власну швидкість?
- З пункту А виїхала легкова машина. Одночасно з пункту В у тому ж напрямку виїхала вантажівка зі швидкістю 50 км/год. Яка швидкість легкової машини, якщо вона наздогнала вантажівку через 7 год і відстань між А і В 168 км?
- За кожну годину автомобіль віддаляється від велосипедиста, якщо вони рухаються в одному напрямі, на 48 км. Одну й ту ж відстань автомобіль може проїхати за 2 год, а велосипедист за 8 год. Які їх швидкості?
- Туристи мали здійснити тригодинну подорож на моторному човні по
річці. На яку відстань вони можуть спуститися униз за течією річки, щоб
своєчасно повернутися назад, якщо швидкість течії 3 км/год, а власна швидкість
човна 24 км/год?
- Власна швидкість моторного човна у 8 разів більша, ніж швидкість чечїі
річки. Яка швидкість течії і власна швидкість човна, якщо рухаючись за тсчіао човен за 4 год долає 108 км? , ,
- Швидкість першого ковзаняра на 2 м/с більша, ніж швидкість другого. Якщо другий ковзаняр стартує па 20 с раніше першого, то перший після початку бігу з того ж місця дожене другого через 80 сек. Які швидкості спортсменів?
- Швидкість пішохода на 8 км/год менша, ніж швидкість велосипедиста. Відстань від пункту А до пункту В велосипедист долає за 2 год, а пішохід за 6 год. Які швидкості пішохода і велосипедиста?
- Відстань між лісосплавними ділянками 600 км. З них одночасно назустріч один одному вийшли два буксири. Швидкість першого була на 10 км/год більша, ніж швидкість другого. Через 3 год відстань між ними була на 180 км більша за ту, на яку вони зблизилися. Які швидкості буксирів?
- Власна швидкість теплохода у 9 разів більша, ніж швидкість течії річки. Які швидкості теплохода і течії річки, якщо відстань в 96 км проти течії теплохід долає за 6 год?
- З пунктів А і В, відстань між якими 150 км, одночасно виїхали назустріч один одному 2 велосипедисти і зустрілися о 9 годині, причому, той, який виїхав з пункту А, проїхав на ЗО км більше. Після зустрічі велосипедисти продовжували рухатися. Велосипедист з пункту А прибув у пункт В о 13 годині. О якій годині прибув у пункт А велосипедист з пункту В ?
- Якщо лижники будуть на відстані 6 км 500 м один від одного і одночасно почнуть зближатися, то вони зустрінуться через 20 хвилин. Якщо ж вони вийдуть одночасно з одного й того ж пункту в одному напрямі, то через 40 хвилин один з них віддалиться від другого на 600 м. Які швидкості лижників?
Додаток Ж
Арифметичні задачі для 5 класу
- З однієї станції в один і той же час вийшли в протилежному напрямку два потяги. Швидкість одного 80 км\год, а швидкість другого 95 км\год. Яка відстань буде між потягами через З год?
- Від седа до міста велосипедист їхав 4 год з і швидкісно 12 км\год. Скільки часу він затратить на зворотній шлях, якщо збільшити швидкість на 4 км\год?
- З двох сіл вийшли назустріч один одному два пішоходи і зустрілись
через 4 г. Відстань між селами 36 км. Швидкість одного пішохода 4 км\год. Знайти швидкість другого пішохода.
- З аеродрому вилетів вертоліт зі швидкістю 210 км/год. Через 2 год з цього ж самого аеродрому за вертольотом вилетів літак, який через 3 год після свого вильоту перегнав вертоліт на S40 км. Знайдіть швидкість літака.
- З однієї і тієї ж пристані в одному і тому ж напрямку відійшли одночасно два теплоходи. Швидкість одного теплохода 22 км/год. швидкість другого 27 км/год. Якою буде відстань між теплоходами через 6 г, через 8 г?
- Відкрили кран, який в хвилину подає ЗО л води, і за 5 хв наповнили ванну. Потім кран закрили і відкрили зливний отвір, через який вся вода вилилась за 6 хв. Скільки літрів води вилилось за 1 хв?
- Коли почалось збирання врожаю з першої ділянки було зібрано 612 т пшениці, з другої ділянки - в 3 рази менше, чим з першого, а з першого - в 4 рази більше, чим з третього. Скільки тон пшениці було зібрано з трьох ділянок?
- Потяг пройшов відстань 336 км за 4 год, а автобус - 126 км за 3 год. У скільки разів швидкість автобуса була менша швидкості потяга?
- Два тесляри заробили разом 140 гр. Один із них робив 14 днів по 7 год в день, другий - 7 днів по 6 год. Скільки грошей заробив кожний тесляр?
- На млин привезли 9600 кг пшениці. При розмелені залишки склали 1200 кг. Муку насипали в мішки і навантажили на 3 машини.І Іа першу машину навантажили ЗО мішків, на другу - 35 мішків, па третю - 40 мішків, Скільки кілограмів муки навантажили на кожну машину, якщо у всіх мішках муки було порівну?
- Для фарбування стін було витрачено 4 однакові банки білої і ще 3 кг зеленої фарби. Всього було витрачено 19 кг фарби. Скільки кілограмів білої було в кожній банці?
- Для перевезення 35 т вугілля було виділено декілька автомаїшіп. 11а кожну машину було навантажено по 4 т вугілля, після чого залишилось перевезти ще 7 т вугілля. Скільки машин було виділено?
- 40 кг білила розлили в декілька банок, потім в кожну банку додали 2 кг червоної фарби. Тоді в кожній банці виявилось 7 кг фарби. Скільки було банок?
- За три год роботи екскаватор вийняв 555 кубічних метрів землі. Скільки кубічних метрів землі вийме другий екскаватор за 4 год роботи, якщо в годину він виймає на 15 кубічних метрів землі менше, чим перший?
- Дві бригади фермерів, працюючи разом, заготовили 1200 т силосу. Кожного дня одна бригада заготовляла 40 т силосу, а друга - 35 т. Скільки еілосу заготовила кожна бригада?
- Один робітник працював 3 дня по 7 год в день, а другий - 2 дня по 8 год.
Разом вони виготовляли 481 деталь. Скільки деталей виготовив кожний робітник, якщо продуктивність праці робітників була однією і тією ж?
- Відстань між селищем і містом 144 км. Скільки часу затратив робітник, щоб дістатись до міста і повернутись назад, якщо в місто він їхав на автобусі зі швидкістю 36 км/год, а назад він проїхав на навантаженій машині зі швидкістю 48 км/год?
- Маса одного метра рейки - 32 кг. Скільки знадобиться залізничних вагонів вантажопідйомністю 60 т, щоб перевезти всі рейки, необхідні для збудування залізничної дороги в одну між двома містами, якщо відстань між ними 180 км?
- З двох станцій, відстань між якими 720 км. вийшли одночасно назустріч один одному два потяти. Швидкість першого 75 км\год, а другого на 10 км/год більше швидкості першого. На якій відстані один в другого будуть потяга через 4год?
- Розв'яжіть за допомогою рівнянь задачу: ”В одному бідоні було 36 л молока коли із нього перелили в інший бідон 4 л, то в цих бідонах молока стало порівну. Скільки літрів молока було в іншому бідоні?"
- Папка дешевше портфеля в 4 рази, тому за неї заплатили на 7 гр.50 к. менше, чим за портфель. Скільки коштує папка?
- Щоб приготувати речовину для шліфування мідних виробів, беручі. 10 частин води, 5 частин нашатирного епірту і 2 частини крейди (по масі). Скільки грамів кожної речовини погрібно взяти, щоб приготувати 340 кг речовиип?
- Для виготовлення бутилочного скла беруть 25 частин піска, 9 частин соди і 5 частин вапна (по масі). Скільки потрібно соди, щоб зробити 390 кг стікла?
- Морозиво складає 7 частин води, 2 частини молочного жиру і 2 частини сахару (по масі). Скільки потрібно сахару для приготування 4 кг400 г морозива?
- При меленні жита отримуємо 6 частин борошна і 2 частини відходів. Скільки одержимо борошна, якщо змолоти 1 тжита?
- Для приготування вишневого варення на 2 частини вишень беруть З частини цукру (по масі). Скільки вишень і скільки цукру пішло на варення, якщо
цукру пішло на 7 кг 600 г більше, чим вишень?
- Піонери трьох загонів зібрали 240 кг насіння рослин. Перший загін зібрав 87 кг, а другий і перший загони разом зібрали 174 кг. Скільки кілограмів насіння зібрав другий загін і скільки зібрав третій?
- У мішку 20 кг крупи. Після того як із нього наповнили декілька пакетів по 3 кг, у мішку залишилось 5 кг. Скільки пакетів наповнили крупою?
- У бідоні 31 л молока. Після того як із нього наповнили двохліірову банку, у бідоні залишилося 7 л. Скільки двохлітрових банок наповнили молоком?
- Площа фізкультурного залу в 6 раз більше площі класної кімнати. Знайти
площу зала, якщо він більше площі класної кімнати на 250 кубічних метрів.
- Відстань від Землі до Сонця дорівнює 150 млн. км. Скільки часу йде на Землю світла від Сонця, якщо за одну секунду він проходить 300 тис.км? Скільки часу знадобиться ракеті, щоб подолати туж відстань, якщо б її швидкість була 15 км/с?
- За одну добу через нещільно закритий кран зі струменя товщиною в сірник втрачається більше 400 л води. Скільки восьмилітрових відер буде втрачено при цьому за місяць (30 днів)?
- 3 10 кг целюлози можливо отримати 750 м віскозної тканини. Із одного кубічного метра деревини можливо отримати 200 кг целюлози. Скільки метрів віскозної тканини можливо отримати із 20 кубічних метрів деревини?
- Собака побачила хазяїна, коли була від нього на відстані 450 м, і побігла до нього зі швидкістю 15 м/с. Яка відстань між хазяїном і собакою буде через 5с,через t с?
- На будівництві робітник міг ущільнити за годину за допомогою ручного вібратора 5 кубічних метрів бетону. Коли застосували трактор з потужними вібраторами, двоє робітників за 7 год стали ущільнювати 630 кубічних метрів бетону. В скільки раз збільшувалась продуктивність праці?
- Теплохід йшов по озеру 3 год зі швидкістю 23 км/год, потім 4 год по річці. Скільки кілометрів пройшов теплохід за ці 7 год, якщо його швидкість по річці на 3 км/год більше, чим по озеру?
- Зараз відстань між собакою і кішкою ЗО м. Через скільки секунд собака дожене кішку, якщо швидкість собаки 10 м/с, а кішки 7 м/с?
- Батько старше сина на 20 років, а сип молодший батька а 5 раз. Скільки років батькові і скільки років сину ?
- Велосипедист рухається назустріч автобусу. Зараз між ними підсини. 60км, і вони зустрінуться через годину. Знайдіть швидкіст ь велосипедне і а, якщо вона менше швидкості автобуса в 4 рази.
- У Василька було в 3 рази більше грошей, ніж у Петрика. Вони склали своі гроші і купили морозиво за 22 копійки, після чого у них залишилося 6 копійок. Скільки грошей було у кожного хлопчика?
Додаток З
Задачі на знаходження відсотків від числа, знаходження числа за його відсотками та знаходження відсоткового відношення чисел
- Учні початкової школи і старшокласники зібрали 8 400 кг металолому. На долю старшокласників припало 65 % зібраного металолому. Скільки металолому зібрали учні початкової школи?
- Засіяли 65 % поля, що складає 325 га. Знайти площу поля.
- В перший день турист пройшов 7 % зазначеного шляху. Після чого йому залишилось пройти 279 км. Який шлях намітив пройти турист?
- В ящику 120 кг пшона. Після того, як з ящика набрали мішок пшона, в ньому залишилося 65 % всього пшона. Скільки пшона ввійшло в мішок?
- Зранку з стоянки виїхало 50 % автомашин. Потім 50 % автомашин, які залишилися, після чого на стоянці залишилося 9 машин. Скільки автомашин було на стоянці зранку'?
- Гри команди зібрали 3 200 кг макулатури. На долю першої припадає 35 % макулатури, на долю другої 30 %. Скільки кілограмів макулатури зібрала третя команда?
- Маса сушених яблук складає 16 % маси свіжих. Скільки потрібно взяти свіжих яблук, щоб отримати 40 кг сушених?
- Коли від мотка дроту відрізали 15 % його довжини, в ньому залишилось 68 м. Скільки дроту було в мотку?
- Надоїли 150 л молока. Дитячий садок отримав 20 % цієї кількості. Решту молока відправили в дві бригади. Одна з них отримала в 3 рази більше, ніж друга. Скільки молока отримала кожна бригада?
- В коробці були кольорові олівці. Спочатку із коробки взяли 50% олівців, а потім 30% залишку. Після цього в коробці залишилось 3 олівці. Скільки олівців було в коробці?
- Треба відремонтувати 210 км дороги. У перший тиждень відремонтували 10% дороги. Скільки кілометрів дороги залишилося відремонтувати?
- Три студентських групи посадили 2800 дерев. Перша група посадила 40% усіх дерев, а друга - 28%. Скільки дерев посадила третя група?
- Маса сушеної картоплі складає 14% маси свіжої. Скільки треба взяти свіжої картоплі, щоб одержати 91 кг сушеної?
- Витративши 35% бензину , що був у баці, шофер побачив, що в бані залишилося 36 л бензину Скільки літрів бензину було в баці спочатку?
- У ящику 160 кг рису. Після того як наповнили рисом із ящика два мішки, у ящику залишилося 25% рису. Скільки рису насипали в кожний мішок, якщо в один із них насипали в 3 рази менше, ніж в інший?
- Витративши 1224 грн. на покупку пальт, покупець зауважив, що в нього залишилося 55% виграшу на квиток «Забава». Скільки грошей робітник виграв на квиток «Забава»?
- Змішали 4 кг сухих яблук і 6 кг сухих грушок. Скільки відсотків суміші складають яблука?
- До початку року до школи привезли 300 підручників і 700 книг для читання. Який відсоток від усіх привезених книг складають підручники?
- У селищі побудували 16 одноповерхових будинків і 4 двоповерхових будтнки. Який відсоток побудованих будинків складають одноповерхові будинки?
- На прибирання території вийшли 160 чоловік. На ремонт дороги відправили 25% усіх людей, а інших розбили на дві бригади саджати дерева. У одній бригаді було в 3 рази більше людей, нж в іншій. Скільки людей було в кожній бригаді?
- Для узвару змішали 3 кг сухих яблук і 7 кг слив. Який відсоток суміші складають сливи?
- На столі лежала пачка зошитів. Спочатку віяли 30% усік юиїлііь. иогім 75% зошитів, що залишилися. Після цього на слові залишилося 1-і зошитів. Скільки зошитів було в пачці спочатку?
- 3 одного пункту в одному напрямі вийшли два автомобілі. Через який час відстань між ними буде 300 км, якщо швидкість одною з них 85 км/ч, а іншого 65 км/ч?
- Мотоцикліст іде слідом за велосипедистом. Швидкість мотоцикліста 64 км/год, а швидкість велосипедиста 12 км/год. Через скільки годин велосипедист буде попереду мотоцикліста па відстані 5 км, якщо зараз між ними 109 км?
Додаток І
Задачі на знаходження невідомого доданка за їхнім кратним відношенням і сумою або різницею
- За шапку і шарф заплатили 25 грн. Скільки коштує шапка, якшо вона дорожча шарфа в 4 рази?
- Маса двох валіз 20 кг. Маса одного з них у 3 рази менше маси другого. Знайти масу кожної валізи.
- В два вагони повантажили 78 т ватажу. В один із них увійшло в 2 рази більше, ніж у другий. Скільки ватажу в кожнім вагоні?
- За два дні машина пройшла 720 км. В перший день вона пройшла в З рази менше, ніж в другий. Скільки кілометрів пройшла машина на другий день?
- Провід довжиною 60 м треба розділити на два шматки так, щоб довжина одного шматка виявилася довшою за іншого в 5 разів. Знайдіть довжину кожного шматка проводу.
- У двох ящиках було 135 кг цвяхів. Причому в першому ящику цвяхів було в 4 рази більше, ніж у другому. Скільки кілограмів цвяхів було в кожному ящику?
- За день туристи пройшли 15 км. Після обіду туристи пройшли в 4 рази мен ше, ніж до обіду. Скільки кілометрів пройшли туристи після обіду?
- Книга містить 280 сторінок і складається з двох розповідей, причому на першу розповідь припадає 3 частини, а на другу 4 частини всієї книги. Скільки сторінок містить перша розповідь?
- Площа двох кімнат 36 м2. Площа однієї з кімнат у 2 раз менша площі іншої. Знайдіть площу кожної кімнати.
- Площа трьох ділянок 3 620 кв.м. Площа першої ділянки на 120 кв.м більше площі другої ділянки, а площа другої в 3 рази менше площі третьої. Знайти площу кожної ділянки.
- Маса трьох чавунів 62 кг. Маса першого в 3 рази, а маса третьою на 12 кг більше маси другого чавуна. Знайти масу кожного чавуна.
- Маса трьох вантажів 156 т. Маса першого вантажу в 4 рази, а маса другого вантажу на 24 т більша маси третього вантажу. Знайдіть масу кожного вантажу.
- Площа трьох кімнат 51 м2. Третя кімната в 3 рази менше першої, а друга кімната на 5 м2 менша першої кімнати. Знайдіть площу кожної кімнати.
- В першій бригаді в 3 рази більше робітників, ніж в другій. Після того як в другу бригаду прийняли ще 10 чоловік, в двох бригадах стало 70 робітників. Скільки робітників було в кожній бригаді?
- В першому парку автомашин в 4 рази менше, ніж у другому. Після того, як перший парк отримав ще 23 машини, в двох парках стало 183 машини. Скільки автомашин було в кожному парку?
- У першому вагоні трамвая було в 3 рази більше пасажирів, ніж у друюму. Після того, як у другий вагон увійшло 45 пасажирів, у двох вагонах стало 89 пасажирів. Скільки пасажирів було в кожному вагоні трамвая спочатку?
- У першій бочці було в 4 рази більше бензину, ніж у другій. Після того як із другої бочки взяли 50 л бензину, у двох бочках стало 270 л бензину. Скільки літрів бензину було в кожній бочці?
Додаток К
Задачі, що розв’язуються методом зображення натуральних чисел у вигляді відрізків
- У Олени, Ніни та Марини разом 40 ляльок. У Олени ляльок на 9 більше, ніж у Ніни, а у Ніни їх на 4 менше, ніж у Марини. Скільки ляльок у кожної з дівчат?
- У Дмитра, Сергія та Олега разом ЗО машинок. У Дмитра в 3 рази більше машинок, ніж у Олега, а у Сергія в 2 рази більше, ніж у Дмитра. Скільки машинок у кожного з хлопців?
- Дідові, батькові та сину разом 121 рік. Батькові разом з сином 44 роки. Син на 28 років молодший за батька. Скільки років діду, батькові та синові?
- Микола та Іван грали в шашки. Іван задумався над своїм ходом, а Микола від нудьги полічив, що на дошці з 64 клітинок пустих клітинок втричі більше, ніж зайнятих, і що у нього на дві шашки більше, ніж у Івана. Скільки шашок було у кожного з них на даний момент?
- У Марини, Олени, Тетяни та Ірини разом 80 зошитів. Скільки зошитів у кожної дівчини, якщо у Марини втричі менше зошитів, ніж у Олени, у Олени втричі менше, ніж у Тетяни, а у Тетяни втричі менше, ніж у Ірини?
- Дідусь з чотирма онуками пішов у ліс по гриби. В лісі, домовившись зустрітися через півгодини на певному місці, вони всі розійшлися у різні боки. Зустрівшись через півгодини, дідусь побачив, що його онуки не знайшли жодного гриба, а він знайшов 45 штук. На прохання онуків дідусь віддав їм усі знайдені гриби. Потім знову розійшлися у різні боки. Один онук знайшов ще 2 гриби, другий — 2 загубив, третій знайшов ще стільки, скільки отримав від діда, а четвертий загубив половину отриманих від діда. Коли діти прийшли додому і полічили свої гриби, то в усіх було порівну. Скільки грибів отримав кожний від дідуся і скільки було у кожного грибів, коли вони повернулися додому?
- Один чоловік мас шість синів. Один від другого старший на 4 роки, а найстарший з синів втричі старший наймолодшого, Скільки років кожному з синів?
- Коли Василя запитали, скільки йому років, він подумав і сказав: «Я втричі молодший за батька, проте втричі старший за брата Антона». Тут підбіг маленький Антон і повідомив, що батько старший від нього на 40 років. Скільки років Василю?
- У спортзалі школи 67 хлопчиків і 41 дівчинка сиділи в три ряди, причому, в кожному ряду була однакова кількість дітей. У першому ряду хлопчиків було в 5 разів більше, ніж дівчаток. У другому — хлопчиків було на 14 більше, ніж дівчаюк. Скільки хлопчиків і скільки дівчаток сиділо в кожному ряду?
Додаток Л
Види діяльності під час вивчення типових задач
|
|
Етапи вивчення типу |
Вид діяльності |
|
І. |
Підготовчо- мотиваційний |
|
|
ІІІ. |
Навчально- операційний |
вирізнения задач даного типу із загального масиву;
|
|
III. |
Перший рівень контролю, оцінювання та корекції
|
- контроль і оцінювання навичок учнів із розв’язування задач неускладнсної структури |
|
ІV. |
Творчо-розвиваючий( розгортання типу) |
-розв’язування парних задач: а)задача даного типу і задача зі схожою математичною структурою; б) задача даного типу і задачі споріднені до неї за способами розв’язування - розв’язування задач підвищеної складності; - виконання творчих завдань; |- розв’язування задач типу нетрадиційними способами
|
|
V
|
Узагальнення та систематизація |
-узагальнення та систематизація знань про типові ознаки і типові способи в курсі алгебри під час вивчення методу рівнянь; -порівняння арифметичного й алгебраїчного розв’язувань даної задачі (визначення їх переваг чи недоліків для конкретного випадку)
|
|
VІ. |
Контроль, оцінювання та корекція другого рівня |
|
1
-
Позитивним у розробці є те, що автор наводить типові задачі з рішенням. Дякую за чудову розробку.


про публікацію авторської розробки
Додати розробку
