Оволодіння властивостями функцій

Оволодіння властивостями функцій

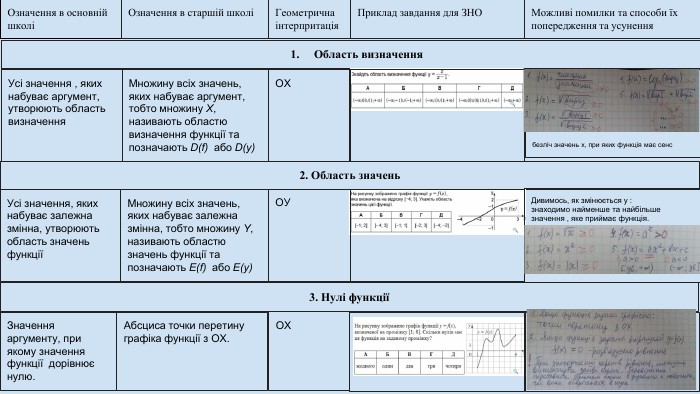
Означення в основній школіОзначення в старшій школіГеометрична інтерпритація. Приклад завдання для ЗНОМожливі помилки та способи їх попередження та усунення. Область визначення. Усі значення , яких набуває аргумент, утворюють область визначення. Усі значення, яких набуває залежна змінна, утворюють область значень функції 2. Область значень3. Нулі функціїЗначення аргументу, при якому значення функції дорівнює нулю. Множину всіх значень, яких набуває аргумент, тобто множину Х, називають областю визначення функції та позначають D(f) або D(y)Множину всіх значень, яких набуває залежна змінна, тобто множину Y, називають областю значень функції та позначають E(f) або E(y)ОХбезліч значень х, при яких функція має сенс. ОУДивимось, як змінюється y :знаходимо найменше та найбільше значення , яке приймає функція. Абсциса точки перетину графіка функції з ОХ. ОХ

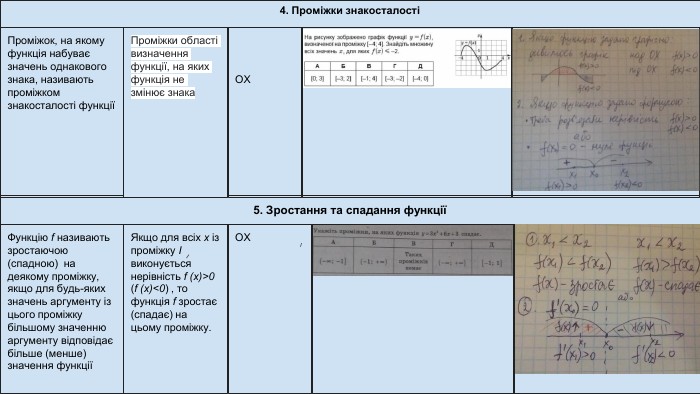
4. Проміжки знакосталості5. Зростання та спадання функціїПроміжок, на якому функція набуває значень однакового знака, називають проміжком знакосталості функціїФункцію f називають зростаючою (спадною) на деякому проміжку, якщо для будь-яких значень аргументу із цього проміжку більшому значенню аргументу відповідає більше (менше) значення функціїЯкщо для всіх х із проміжку І виконується нерівність f (x)>0 (f (x)<0) , то функція f зростає (спадає) на цьому проміжку. Проміжки області визначення функції, на яких функція не змінює знака. ОХОХ

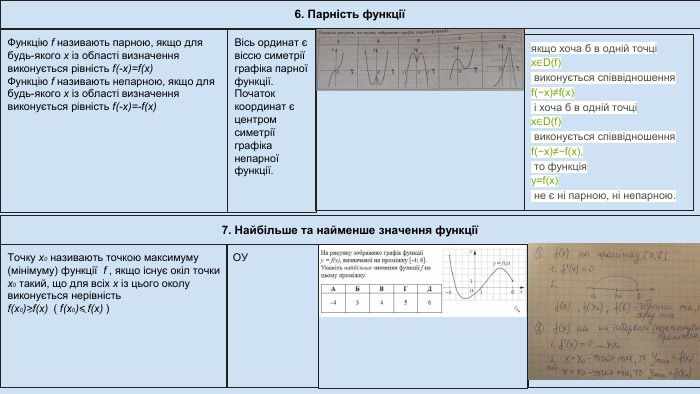
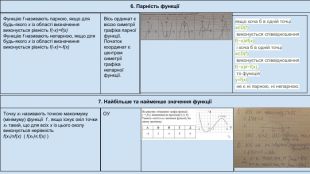
6. Парність функції7. Найбільше та найменше значення функціїФункцію f називають парною, якщо для будь-якого х із області визначення виконується рівність f(-x)=f(x)Функцію f називають непарною, якщо для будь-якого х із області визначення виконується рівність f(-x)=-f(x)Вісь ординат є віссю симетрії графіка парної функції. Початок координат є центром симетрії графіка непарної функції. Точку х0 називають точкою максимуму (мінімуму) функції f , якщо існує окіл точки х0 такий, що для всіх х із цього околу виконується нерівність f(x0)>f(x) ( f(x0)< f(x) )якщо хоча б в одній точці x∈D(f) виконується співвідношення f(−x)≠f(x) і хоча б в одній точці x∈D(f) виконується співвідношення f(−x)≠−f(x), то функція y=f(x) не є ні парною, ні непарною. ОУ

Завдання з вибірковою відповіддю1. 5.2. 6. 3. 7.4.

5 завдань для письмового розв'язання1.2.3.

4.5.

Дякую за увагу!