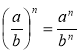Означення степеня з цілим від'ємним показником

Тема. Означення степеня з цілим від'ємним показником

Мета: домогтися засвоєння учнями змісту означення степеня з ці­лим від'ємним показником (для цілої та дробової основи степеня); сформувати вміння відтворювати означення степеня та застосовувати його для перетворення степеня з цілим від'ємним показником у дріб, та навпаки, сформувати вміння розв'язувати вправи на обчислення значень числових виразів із застосуванням вивченого означення степеня з цілим показником.

Тип уроку: засвоєння знань та первинних умінь.

Наочність та обладнання: опорний конспект «Степінь з цілим від'ємним показником».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Вчитель збирає зошити для перевірки виконання учнями аналізу тематичної контрольної роботи за розданими розв'язаннями (див. вище).

III. Формулювання мети і завдань уроку, мотивація навчальної діяльності учнів

Традиційно уявлення про можливість існування степеня з цілим від'ємним показником формується у зв'язку з розширенням поняття степеня з натуральним показником. Проте свідомому розумінню не­обхідності такого розширення можуть сприяти, по-перше, звертання до довідкової літератури, що містить записи значень деяких констант у стандартному вигляді з від'ємним показником, а по-друге, виконан­ня логічних вправ на порівняння та узагальнення. Наприклад, можна запропонувати учням продовжити числові ряди (один з яких скла­дається зі значень степенів деякого числа, а другий складається із са­мих відповідних степенів):

1-й ряд: 1000, 100, 10, і, 0,1, 0,01, 0,001, ...

2-й ряд 10³, 10², 10¹, 10⁰, ...

Після виконання порівняння на етапі узагальнення формулюється проблема — між існуючим уявленням про степінь (із натуральним показ­ником) та необхідними для обчислень потребами. Подолання цього про­тиріччя є водночас і мотивом, і метою навчальної діяльності учнів на уроці.

IV. Актуалізація опорних знань та вмінь

 З метою успішного сприйняття учнями навчального матеріалу перед його вивченням слід активізувати такі знання і вміння учнів: означення степеня з натуральним показником; основна властивість степеня та її наслідки, а також їх застосування для обчислення значень числових виразів та для перетворення ви­разів, що містять множення, ділення степенів з однаковими основами та піднесення степеня, добутку та частки виразів до степеня.

Виконання усних вправ

1. Подайте у вигляді добутку дроби: ; ; ; .
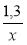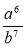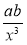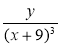2. Прочитайте вирази, назвавши основу і показник степеня; 6⁴; (2,1)⁹; .
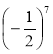3. Обчисліть значення виразів:

а) піднесіть до квадрата: 3; -5; ; ; ; 0,8;

б) піднесіть до куба: 2; -3; ; ; ; - 0,3.

4. Визначте знак виразів, назвавши основу і показник степеня:

6⁴; (2,1)⁹; 10¹; (-7)⁵; 0¹²; .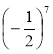

5. Визначте знак виразів, не виконуючи піднесення до степеня:
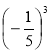   ; ; (-2)¹⁰; -2¹⁰; (-3)⁹; -3⁹; ; .
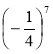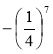6. Укажіть порядок дій в обчисленні значення виразів:

15² – 3⁴; 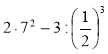; (3² – 2³)²⁰.

V. Засвоєння знань

План вивчення нового матеріалу

1. Означення степеня з цілим від'ємним показником.
2. Запис означення степеня з цілим від'ємним показником для випад­ку основи, що має вигляд .
3. Приклади застосування означення степеня з цілим від'ємним по­казником для обчислення значення виразу, що містить степінь.

 Після проведеної роботи на етані визначення мети уроку до­статньо узагальнити проведені спостереження і сформулювати їх у вигляді формули , п N, де а ≠ 0, (а також, можливо, у словесному вигляді: степінь із цілим від'ємним показником і з основою, відмінною від нуля, дорівнює дробу, чисельник яко­го – одиниця, а показник – степінь з тією самою основою і про­тилежним даному (натуральним) показником; однак вимагати від учнів відтворення цього формулювання не слід). При цьому необхідно звернути особливу увагу учнів на те, що степінь із цілим від'ємним показником має зміст лише при ненульовому значенні основи степеня, тому, на відміну від степеня з нату­ральним показником, степінь числа 0 з цілим від'ємним показ­ником не має змісту (див. опорний конспект).

Оскільки для розв'язування багатьох завдань корисним є означен­ня степеня з цілим від'ємним показником, записане на випадок, якщо основа с дробом вигляду , тому одразу по закінченні розгляду при­кладів на пряме застосування означення степеня з цілим від'ємним показником учитель або пропонує учням у вигляді завдання, або разом з учнями виводить означення степеня з цілим від'ємним показником для степеня з основою (а ≠ 0, b ≠ 0): 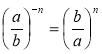. Розглядаючи питання про сферу можливого застосування вивченого означення, слід звернути увагу учнів на гой факт, що обчислення значень виразів, які містять серед інших арифметичних дій дію піднесення числа до степе­ня, слід пам'ятати про існуючий порядок виконання дій різного ступе­ня, а також про те, що під час обчислення значення степеня з цілим від'ємним показником спочатку застосовується означення степеня, а потім обчислюється значення степеня з натуральним показником (за означенням степеня з натуральним показником).

VI. Формування вмінь

Виконання усних вправ

1. Обчисліть: 2⁴; (-3)²; (0,1)³; (-1)⁸; 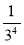; ; 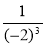(-15)⁹; 0,3⁰; 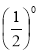; 0⁰.
2. Замініть дробом степінь із цілим від'ємним показником. Заповніть пропуски.

; ; ; .

3. Замініть дріб степенем із цілим від'ємним показником:

; ;  ; 

Виконання письмових вправ

Для реалізації дидактичної мети на цьому уроці слід розв'язати за­вдання такого змісту:

1. Запис степеня із цілим від'ємним показником у вигляді дробу, і на­впаки.

1) Замініть степінь із цілим від'ємним показником дробом:

а) 10^-6; б) 9^-2; в) а^-1; г) х^-20; д) (ab)^-3; є) (а + b)^-4.

2) Замініть дріб на степінь з цілим від'ємним показником:

а) ; б) ; в) ; г) ; д) .

2. Запис числа у вигляді степеня із заданою основою.

1) Подайте числа 4, 8, 16, 32, 2, 1, ,,, у вигляді степеня з основою 2.

2) Подайте числа:

а) 8, 4, 2, 1, , і у вигляді степеня з основою 2;

б) , , , 1, 5, 25, 125 у вигляді степеня з основою 5.

3. Обчислення значень числового виразу (то має вигляд степеня з ці­лим від'ємним показником або містить такий степінь).

1) Обчисліть: 9^-2; 15^-1; 3^-3; 5^-4; 12⁰; (-2)^-4; (-3)^-3; 0,5^-2.

2) Знайдіть значення виразу:

а) 5 ∙ 10²; б) 16 ∙ 2^-5; в) 5^-3 : 25⁰; г) 3 : 2^-3; д) 2^-4 +2^-2;

е) 2^-3 – 2^-4; ж) 6^-1 + 3∙3^-2; з) 4^-1 – 3^-2.

3) Знайдіть значення виразу:

а) 256 ∙ 2^-8; б) 0,1^-2 + (-1)^-24; в) 1,5^-3 : 2,5^-2; г) ;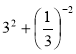

д) ; є) .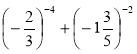

4) Знайдіть значення виразу:

а) 1^-1 + 2^-1 + 3^-1 + 4^-1; б) ;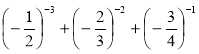

в) 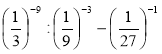; г) (2 + 2^-1)^-2 – (2 + 2^-2)^-1.

4. Порівняння з нулем значення виразу.

1) Порівняйте з нулем значення степеня:

а) 9^-5; б) 2,6^-4; в) (-7,1)^-6; г) (-3,9)^-3.

5. Запис у вигляді раціонального дробу виразу зі змінними, що міс­тить степінь із цілим від'ємним показником.

1) Подайте вираз у вигляді раціонального дробу:

a) 4а^-2b^-1; б) 7^-1ab^-5; в) х^-2у^-3; г) (а + b)^-2.

2) Спростіть вираз:

а) (а + 5)^-2(3а + 15); б) (а^-2 – b^-2) : (a + b); в) (b – 4)^-1 – (b + 4)^-1;

г) (x^-3 – y^-3) : (х² + ху + y²); д) 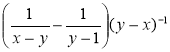; е) .

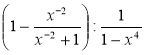6. Логічні вправи та завдання підвищеного рівня складності для учнів,
   які мають достатній та високий рівні знань.

1) Подайте у вигляді дробу вираз:

а) ху^-2 – х^-2у; б) 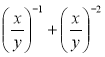; в) тп(п – т)^-2 – (m – п)^-1; г) (х^-1 + у^-1)(х^-1 – у^-1).

2) Спростіть вираз: а) ; б) .

3) Який вираз пропущено?

7. На повторення використання властивостей степеня з натуральним показником:

1) Запишіть у вигляді одночлена стандартного вигляду вираз:

а) -5х³у² ∙ 2ху³; б) (-3a²b⁴)²; в) (-2xy⁵)³; г) (m⁴n³)² ∙ (-mn)³.

2) Знайдіть значення виразу:

а) 5⁵ ∙ 2³; б) 4⁴ ∙ 1,25⁴ ∙ 2⁴; в) 0,5⁹ ∙ (2³)²; г) 2,5⁵ ∙ 0,7² ∙ 0,4⁵.

 Вправи до уроку спрямовані на засвоєння учнями сформульо­ваного означення, а також на формування вміння переходити від запису, що містить цілий від'ємний показник, до запису, що містить дріб (із протилежним натуральним показником), і навпаки. Цьому сприятиме виконання учнями вправ із пря­мою вказівкою на виконання зазначених дій та обчислення значення виразу, а також дослідницькі вправи (див. вище).Роз­в'язання вправ на повторення — на застосування властивостей степеня з натуральним показником — сприятиме підготовці учнів до вивчення відповідних властивостей степеня з цілим від'ємним показником.

VII. Підсумки уроку

В якому з випадків правильно виконано дію?

а) 3^-2 = 3²; б) ; в) ; г) .

VIII. Домашнє завдання

1. Вивчити означення степеня з цілим від'ємним показником, а також властивості, отримані під час виконання письмових вправ.
2. Розв'язати вправи на застосування означення та сформульованих на уроці властивостей.
3. Повторити основну властивість степеня з натуральним показником та її наслідки, розв'язати вправи відповідного змісту.