Властивості степеня з цілим від'ємним показником

Тема. Властивості степеня з цілим від'ємним показником

Мета: вивчити властивості степеня з цілим від'ємним показником та сформувати вміння використовувати їх для розв'язування вправ на обчислення значень числових виразів і перетворень виразів зі змінними.

Тин уроку: засвоєння знань та первинних умінь.

Наочність та обладнання: опорний конспект «Степінь з цілим від'ємним показником».

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

Дня перевірки якості первинних знань учнів можна провести математичний диктант або, в разі необхідності, роботу з перевірки домаш­нього завдання за зразком із наступною корекцією.

Математичний диктант

1. Доповніть речення:

Якщо b ≠ 0 і п — натуральне число, то b^-n = ...

2. Як записати 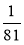у вигляді степеня з від'ємним показником?
3. Запишіть у вигляді дробу: 5^-3; 7^-1 ∙ 7; (ab)^-2; ab^-2.
4. Обчисліть значення виразу: 2^-3 + 3^-2.

III. Формулювання мсти і завдань уроку

Повторивши на етапі перевірки домашнього завдання означення степеня з цілим від'ємним показником і властивості степеня з нату­ральним показником, проводимо паралель між поняттями та форму­люємо проблему, яку слід дослідити на уроці: «Чи існують властивості степеня з цілим від'ємним показником, і якщо існують, то чи не ана­логічні вони властивостям степеня з натуральним показником?» Зро­зуміло, що відшукання розв'язання проблеми і становить основну дидактичну мету уроку.

IV. Актуалізація опорних знань та вмінь

 З метою успішного сприйняття учнями навчального матеріалу перед вивченням нового матеріалу слід активізувати такі знан­ня і-вміння учнів: застосування означення степеня з натураль­ним та цілим показниками для обчислення значень степенів числових виразів; змісту та способами застосування основної властивості степеня з натуральним показником та її наслідки для перетворення цілих раціональних виразів; порядок виконання арифметичних дій різного ступеня.

Виконання усних вправ

1. Яке число слід піднести до квадрата, щоб дістати: 9; 81; 0; 16; ?

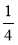Яке число слід піднести до куба, щоб дістати: 8; -27; ; -0,064?

2. Подайте вирази у вигляді степеня:

х⁵х⁷; 5 ∙ 5²; аа³; у⁴у⁶у; 10² ∙ 10 ∙10³; 7² ∙ 49³; а⁸ : а²; 3⁴ : 3; х⁶ : х; ;

а^2п ∙ а^п; (а³)²; 3² ∙ а²; а⁵ ∙ (а¹² : а²)²; -z⁶ : (-z)³.

3. Знайдіть значення виразів: 2³; 2^-3; 5²; 5^-2; 7²; 7^-2; 5³ : 5² – 5 ∙ 2^-3.

V. Засвоєння знань

План вивчення нового матеріалу

1. Формулювання і доведення властивостей степеня з цілим від'єм­ним показником.
2. Приклади застосування властивостей степеня з цілим показником.

 Після того як учні засвоїли означення степеня з цілим від'єм­ним показником, переходимо до вивчення властивостей степе­ня з цілим від'ємним показником. При цьому робимо акцент на тому, що для степеня з цілим показником виконуються ті самі властивості, що й для степеня з натуральним показником (єдине обмеження пов'язане із ОДЗ виразу а^-п,     п Z). Ці влас­тивості формулюються в загальному вигляді, а спосіб їх дове­дення демонструється на прикладі множення степенів з цілими
від'ємними показниками і однаковими основами.

Розглядаючи питання про спосіб застосування властивостей степе­ня з цілим показником, учні мають усвідомити, що дії над степенями з цілими показниками виконуються за тими самими алгоритмами, що й дії зі степенями з натуральними показниками; також можливе їх ви­користання під час виконання дій над степенями з однаковою осно­вою, що не дорівнює нулю, та показниками, один з яких може бути на­туральним, а інший (інші) — цілим від'ємним.

VI. Засвоєння вмінь

Виконання усних вправ

1. Подайте у вигляді степеня вирази: b³Ь^-6; (b²)^-3; (b^-5)⁰.
2. Знайдіть значення виразів: (1,7)² – (1,7)^-2; 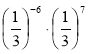; (-5)⁷ ∙ (-5)^-6.
3. Спростіть вирази: t^-3 : t^-5; a^-2 ∙ а³; (z^-3)^-2; (а^-1b^-4)^-2.

Виконання письмових вправ

Для реалізації дидактичної мсти уроку слід розв'язати завдання та­кого змісту:

1. Обчислення значень числових виразів (попередньо застосувавши
   відповідну властивість степеня).

1) Обчисліть: а) 2^-3 ∙ 2²; б) 3^-4 : 3^-3; в) 5^-8 ∙ 5⁸; г) 4³ : 4⁵; д) (8^-1)^-1;

 е) (7^-1)²; ж) 2^-2 ∙ 5^-2; з) .

2) Знайдіть значення виразу: а) 3^-4 ∙ 3⁶; б) 2⁴ ∙ 2^-3; в) 10⁸ ∙ 10^-5 ∙ 10^-6;
г) 2¹⁰ : 2¹²; д) 5^-3 : 5^-3; е) 3^-4 : 3; ж) (2^-4)^-1; з) (5²)^-2 ∙ 5³; и) 3^-4 ∙ (3^-2)^-4.

2. Подання виразів у вигляді степеня з даною основою (степені або ма­ють однакову основу, або потребують переходу до однієї основи,/.

1) Подайте вираз у вигляді степеня з основою а:

а) а³ : а^-7 ∙ а⁵; б) а^-4 ∙ а⁶ : а⁹; в) (a^-2)⁵ : a³; г) а¹⁷ ∙ (а⁸)^-2.

2) Подайте вираз (x^-8) : х¹⁴ у вигляді степеня з основою х і знай­діть його значення при х = 0,1.

3. Спрощення виразів.

1) Подайте у вигляді виразу, який не містить степеня з від'ємним показником:

а) 5ху^-3 ∙ 0,4х^-4у; б) (0,04x^-1) ∙ 5^-2х⁵; в) 3m⁵п¹⁷ – 0,12т^-1п¹⁹;

г) 81²а^-2b^-3 ∙ (3а^-1b^-2)^-4; д) 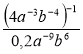; є) .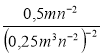

2) Знайдіть значення виразу:

а) 0,2а^-2b⁴ ∙ 5а³b^-3 при a = - 0,125, b = 8;

б) a^-1b^-5 ∙ 81a²b⁴ при а = ,b = .

3) Спростіть вираз і знайдіть його значення:

а) 1,6х^-1y¹² ∙ 5x³y ^-11 при х = - 0,2, у = 0,7;

б) х ^-3 у ^-3 ∙ 30х³ у ^-4 при x = 127, у = .

4. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.

1) Подайте вираз у вигляді степеня з основою 10 (n – ціле):

а) 100ⁿ; б) 0,1 ∙ 100ⁿ⁺³; в) 0,01ⁿ ∙ 10^2-2n.

2) Спростіть вираз (n – ціле): а) ; б) .

3) Подайте вираз х ^-2 + х ^-1 + х  у вигляді добутку двох множників, один з яких дорівнює: а) х; б) x ^-1; в) х².

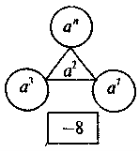
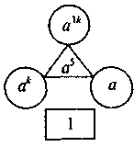
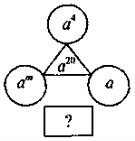
4) Яке число пропущене:

5. На повторення вправи, що передбачають перетворення раціональ­них виразів.

1) Спростіть вираз:

а) 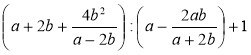; б) .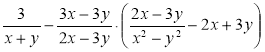

VII. Підсумки уроку

В якому з випадків правильно виконано дію?

1) a¹⁵ ∙ а ^-3 = а ^-5; 2) m^-12 : m^-8 = m⁸; 3) (m^-3)^-5 = m¹⁵; 4) .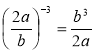

VIII. Домашнє завдання

1. Вивчити властивості степеня з цілим від'ємним показником та ал­горитми їх застосування.
2. Розв'язати вправи на застосування вивчених властивостей (змісту і рівня складності), подібних до вправ класної роботи.
3. Повторити правило множення і ділення числа на розрядну одини­цю (10, 100, 1000,... і 0,1, 0,01, 0,001,...), означення степеня з цілим від'ємним показником, виконати вправи на застосування повто­рених властивостей.