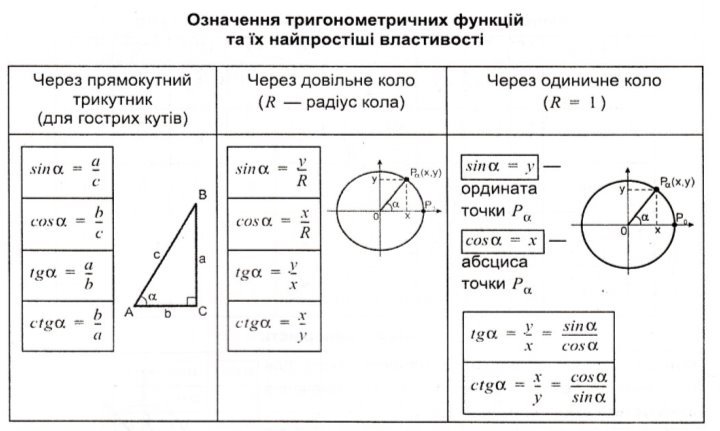
Означення тригонометричних функцій

Підготувала

вчитель математики

Тяпчанського НВК

Долинського району

Владика Руслана Дмитрівна

 

СИНУС І КОСИНУС. ТАНГЕНС І КОТАНГЕНС КУТА.                                                                                              

 

Мета урок.

Навчальна - ввести поняття   “одиничне коло”, “тригонометричні функції кута”;

• вивчити поведінку тригонометричних функцій в  чвертях,  

Виховна  - виховувати культуру мовного спілкування   в ході бесіди, формувати спецлексику, активну громадянську позицію,  навики самостійно приймати рішення; розвивати творчий та естетичний потенціал, критичне мислення учнів.

Розвиваюча - розвивати в учнів вміння практичної реалізації  системи знань в систему вмінь та предметних компетенцій, вміння реалізовувати  прикладні зв’язки через систему курсу математики з  фізикою, астрономією,  внутріпредметні зв’язки курсу математики.

 

Міжпредметні зв’язки.

Забезпечуючі.  Геометрія 8 клас. Т.4. Розв’язування прямокутних  трикутників

                              Геометрія 9 клас.  Т.1. Розв’язування   трикутників

Забезпечувані.  Фізика. Т.1.Гармонійні коливання.    Т.2Динаміка.          Т.3. Оптика       Астрономія.Т.2. Астрономічні дослідження

 

Забезпечення урок.

1.        Література. Г.П.Бевз,  Математика  10 клас
2.        Наочні посібники. Презентації: “Градусна міра кута“, ”Тригонометричні функції кута”
3.        Роздатковий матеріал. Таблиця ”Основні формули тригонометрії”

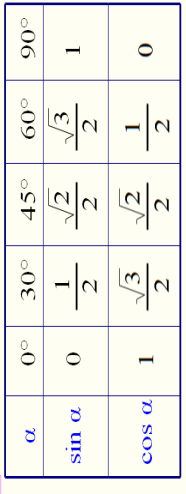
Таблиця значень тригонометричних функцій в деяких кутах.

4. Технічні засоби навчання. Мультимедійний проектор.

 

Компетенції. Навчальна, соціально – трудова, стимулювально – мотиваційна.

Функції:

Теоретична : знати: поняття “радіанна та градусна міри кута”, “одиничне коло”, “тригонометричні функції числового аргументу”, знаки тригонометричних функцій на чвертях, монотонність тригонометричних функцій на чвертях.

Практична: вміти:

 

 

 

 

 

 

 

пг

 

Немає жодної сфери математики, яка

коли – не будь не знайде застосування

для вивчення явищ реального  світу

М.І. Лобачевський

Хід урок

1. Організаційна частина.(Метод:  психолого – педагогічна підтримка роботи учнів на уроці) 2 хв.

Розминка.   Вправа «Програмування себе на успіх»

Слава, успіх, визнання... Напевно, кожен із вас відчував, що то за щастя, коли все вдається. У такі дні ви відчуваєте в себе за спиною крила, а в тілі надзвичайну легкість. Піднесіть руки ті, в кого були такі відчуття.

Спробуйте згадати те надзвичайне відчуття польоту, нехай ваше тіло зазвучить мелодією – і успіх вам забезпечений! І обов'язкова умова – ніколи не втрачайте надії!

На шляху до успіху вам допоможуть настанови:

•    Є те, що я вмію робити краще за інших.

•    Успіх – мій природний стан.

•    Я процвітаю!

•    Я завжди максимально викладаюся на своїй роботі.

•    Я – успішна людина. Мені вдається все, за що я беруся.

•    Усе, що відбувається, – для мого блага. Уже зараз закладаються найщасливіші можливості для мене.

 

Вправа «Абетка добра»

До кожної літери слова «тригонометрія» підібрати добре слово.

Наприклад:   Т – толерантність.  Р – радість. О – освіченість. М – милосердя. Е – елегантність . Т – талановитість.  

 

2. Підготовка до урок.(Метод:  інструктування).

1. Оголошується тема,  мета та завдання урок.

      Тема урок: СИНУС І КОСИНУС. ТАНГЕНС І КОТАНГЕНС КУТА.

 План уроку.

1. Одиничне коло.

2.Означення синуса числового аргументу. Монотонність та знаки синуса на чвертях. Періодичність синуса.

3. Означення косинуса числового аргументу. Монотонність та знаки синуса на чвертях. Періодичність косинуса.

4. Означення тангенса. Лінія тангенсів.

5. Означення котангенса. Лінія котангенсів.

6. Таблиця значень тригонометричних функцій для деяких кутів

 

2. Мотивація пізнавальної діяльності учнів.  (метод – історично - довідниковий).

       Вавілоняни вже на початку  III тисячоліття до н.е. мали календар з розподілом року на 12 місяців. Отже вони вміли визначати положення сонця і зірок на небосхилі, тобто володіли певними знаннями тригонометричного характеру.

Велике значення для розвитку тригонометрії в період її зародження мали праці грецьких учених.

Протягом тисячі років тригонометрія була підсобною наукою у астрономії.

Складалися нові таблиці, знаходилися нові залежності між тригонометричними функціями, за допомогою яких розв’язувалися складні задачі, але тригонометрія залишалася тільки частиною астрономії, самостійної науки не існувало.

 

     Наприкінці ХV ст. італійський мандрівник Христофор Колумб відкрив узбережжя Америки. Слідом за ним туди зробив кілька подорожей інший італієць – Америго Віспуччі.

Португалець Васко да Гама відкрив морський шлях на Індію.

Незабаром кораблі Магеллана вперше в історії зробили навколосвітню подорож.

 Почалася епоха великих географічних відкриттів, завоювань нових територій, освоєння незліченних багатств нових земель.

Не тільки окремі групи купців і мореплавців, але і цілі держави боролися за право експлуатації нових земель. Потрібні були більш потужні і швидкохідні судна, точні географічні карти, досконалі способи орієнтування в відкритому океані.

Все це і багато чого іншого привело до необхідності розвивати астрономію – науку про рух небесних тіл, а розвиток астрономії був неможливий без розвитку тригонометрії.

Перші кроки тригонометрії

Слово “тригонометрія” складається із двох грецьких слів: “триганон” – трикутник і “метрайн” – вимірювати. У буквальному значенні “тригонометрія” означає “вимір трикутників”.

Астрономія, а разом з нею і тригонометрія виникли і розвивалися в народів з розвиненою торгівлею і сільським господарством: у вавілонян, греків, індійців, китайців. Зародилася вона багато століть тому. Про це ми можемо не тільки здогадуватись.

В одному з китайських рукописів, що був написаний близько 2637 року до н.е., є відомості з астрономії, де застосовуються обчислення тригонометричного характеру.

Внесок Ейлера в тригонометрію.

Завершальний етап у розвитку тригонометрії пов'язаний з ім’ям Леонарда Ейлера.

Уроки астрономії, географії і морехідні науки неможливі без застосування тригонометрії. Але до початку XVIII ст.  вона була наукою неопрацьованою, часто незручною в роботі, що іноді призводило до помилок через плутанину в знаках тригонометричних функцій у різних чвертях кола. Кожна формула виводиться з креслення і всі міркування записувалися словесно. Це змусило Ейлера переглянути доведення тригонометричних формул. Він упорядкував питання про знаки тригонометричних функцій у різних чвертях, ввів однакове позначення сторін трикутника: а, в, с і протилежних кутів А, В, С.

Ейлер розробив тригонометрію як науку про тригонометричні функції, запропонував розглядати тригонометричні функції як числа, що виражають відношення відповідних тригонометричних ліній до радіуса кола.

У працях Ейлера тригонометрія набула сучасного вигляду. На підставі його робіт були укладені підручники з тригонометрії, що викладають її в строгій науковій послідовності.

 

      Тригонометричні функції означені у курсі математики як функції кута. Водночас різні задачі з математики, фізики, економіки та інших наук приводять до тригонометричних функцій, аргументами, яких є не кути, а інші величини (довжина, час, температура тощо). Тому в математиці тригонометричні функції розглядають як функції числового аргументу, які в першу чергу використовують для опису різноманітних періодичних процесів.

  Періодичними називаються процеси, для яких характерним є повторюваність подій, значень розглядуваних величин. Схід та захід Сонця, коливання маятника, обертальний рух колеса, заповнюваність міського транспорту – все це приклади періодичних процесів. Відповідно, періодичними називаються функції, які повторюють свої значення через певні проміжки зміни аргументу.

 4. Актуалізація опорних знань учнів.(Метод : встановлення відповідностей)

    №1.  Для елементів прямокутного трикутника встановити відповідність:

А)   sinα                         А) відношення протилежного катета до прилеглого

Б)   cosα                         Б) відношення протилежного катета до гіпотенузи

В)   tgα                          В) відношення прилеглого катета до протилежного

Г)   ctgα                         Г) відношення гіпотенузи до прилеглого катета

                                      Д)  відношення прилеглого катета до гіпотенузи

Очікувана відповідь:

А)   sinα                         А) відношення протилежного катета до прилеглого

Б)   cosα                         Б) відношення протилежного катета до гіпотенузи

В)   tgα                          В) відношення прилеглого катета до протилежного

Г)   ctgα                         Г) відношення гіпотенузи до прилеглого катета

                                      Д)  відношення прилеглого катета до гіпотенузи

Слайдер 2

Висновок 1 (роблять учні): Значення , и гострого кута прямокутного трикутника від довжини сторін не залежать, а залежить від величини кута.

Слайдер 3.

3. Вивчення нового матеріалу.(методи – пояснювально – ілюстративний, навчальний тренажер, опора на життєвий досвід).

 1. Одиничне коло.(самостійне вивчення, презентація)(Метод проектів)

Градусна міра кута

 Ще в Древньому Вавилоні задовго до нашої ери жерці вважали, що свій  денний шлях сонце проходить за 180 кроків, а значить один крок складає 1/180   розгорнутого кута.

У Вавилоні  була прийнята шістдесяткова система числення, тобто фактично числа записувались у вигляді суми степенів числа 60, а не 10.

        Тому зрозуміло, що для більш дрібніших одиниць вимірювання кутів один

 “крок ” послідовно ділиться на 60 частин.  А саме слово “градус” походить від латинського gradus  (крок, сходинка). Секунда перекладається як “друга”.    

Між градусами, хвилинами і секундами існують співвідно­шення: 1º = 60', 1' = 60'',

1' = , 1' = .

Одиничне коло Слайдер 4.

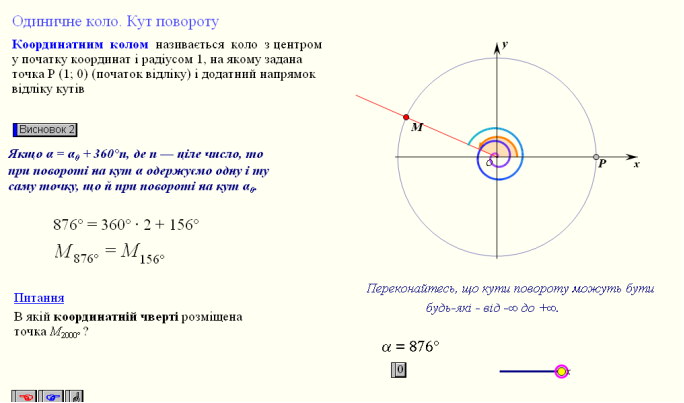
Координатним  колом  називається  коло  з центром у початку координат і радіусом 1, на якому задана точка Р (1; 0) (початок відліку) і додатний напрямок

відліку кутів. При  повороті початкового радіуса  навколо  центра О на кут точка Р(1; 0) перейде у точку М (х; у).

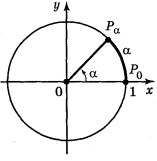
Розглянемо на координатній площині коло радіуса 1 з центром у початку коорди­нат, яке називається одиничним (рис. 3). Позначимо точку Р_о — правий кінець горизонтального діаметра. Поставимо у від­повідність кожному дійсному числу α точку кола за такими правилом:

1) Якщо α > 0, то, рухаючись по колу із точки Р_о в напрямі проти годинникової стрілки (додатний напрям обходу ко­ла), опишемо по колу шлях довжи­ною а, кінцева точка цього шляху і буде шуканою точкою Ρ_α.

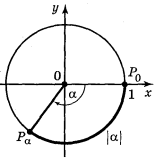
2) Якщо α < 0, то, рухаючись із точки Ρ_о (рис. 4) в напрямі за годинниковою стрілкою, опишемо по колу шлях дов­жиною |α|; кінець цього шляху і буде шукана точка Р_α.

3) Якщо α = 0, то поставимо у відповідність точку Р_о.

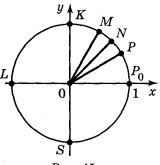Таким чином, кожному дійсному числу можна поставити у відповідність точку Ρ₀ одиничного кола.

Якщо α = α_о + 360⁰n, де n — ціле число, то при повороті на кут α одержуємо одну і ту саму точку, що й при повороті на кут α_о.

Якщо точка Ρ відповідає числу α, то вона відповідає і всім числам виду α + 360⁰n, де 2π — довжина кола (бо радіус дорівнює 1), а де n — ціле число, що показує кількість повних обходів кола в ту чи іншу сторону.

Висновок 2(роблять учні): не залежать  значення тригонометричної функції від додавання до аргументу цілого числа обертів.

Якщо початковий радіус переходить у ра­діус ОМ при повороті на кут а, то в залеж­ності від того, у якій чверті буде радіус 0B, кут α називають кутом цієї чверті.

Так, якщо 0° < α < 90°, то α – кут І чверті;

 якщо 90° < α < 180°, то α — кут II чверті;

якщо 180° < α < 270°, то α — кут III чверті;

якщо 270° < α < 360°, то α — кут IV чверті.

Кути 0°; ±90°; ±180°; ±270°; ±360° не відно­сяться ні до якої чверті.

Слайдер 5.

2. Означення синуса числового аргументу. Монотонність та знаки синуса на чвертях.(Методи: пояснення, ілюстрації, інформаційно - комунікативний)

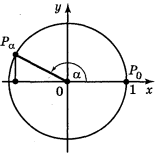
      Синусом числа α називається ордината точки Р_α, утвореної пово­ротом точки Р_α (1; 0) навколо початку координат на кут в α раді­ан (позначається sin α) (рис. 7)

    Синус визначений для будь-якого числа α.

Значення синуса змінюється від  (-1) до 1, тобто

 

 

3. Означення косинуса числового аргументу. Монотонність та знаки косинуса на чвертях. Періодичність косинуса. ( Метод:  пояснювально- ілюстративний)

    Косинусом числа α називається абсциса точки Р_α, утвореної по­воротом точки Р_α (1; 0) навколо початку координат на кут в α градусів(позначається cos α)

    Косинус визначений для будь-якого числа α.

Значення косинуса змінюється від  (-1) до 1, тобто  

Робота з тригонометричним колом на міліметровому папері.

Для знаходження функції:

1. Знаходимо відповідний кут.
2. Ставимо перпендикуляр до осі sin (cos) або продовжуємо радіус-промінь до перетину з віссю tg (ctg).
3. Читаємо відповідь.

 

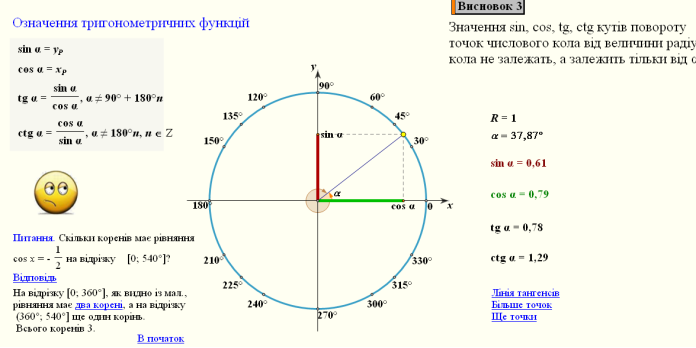
Висновок 3 (роблять учні): Значення , і кутів повороту точок числового кола від величини радіусу кола не залежать, а залежить тільки від α.

Учитель: Кожному допустимому значенню α відповідає єдине значення  sin α, cos α, tg α, ctg α, тому синус, косинус, тангенс, котангенс є функціями кута α. Їх називають тригонометричними функціями.

 

4.              Означення тангенса. Лінія тангенсів. (Метод: пояснювально-ілюстративний)

Тангенсом числа α називається відношення синуса числа α до його косинуса:   .

Тангенс визначений для всіх а, крім тих значень, для яких               cos α = 0, тобто, α = + πn, n Ζ.

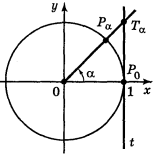
Для розв'язування деяких задач корисно мати уявлення про лінію тангенсів (рис. ). Проведемо дотичну t до одиничного кола в точці Ρ_о. Нехай α — довільне число, для якого cos α 0, тоді точка Р_α (cos α; sin α) не лежить на осі ординат і пряма ОР_α перетинає t в деякій точці Т_α з абсцисою 1. Знайдемо ординату точки Т_α із трикут­ника ОР_оТ_α.

; у = tgα.

Таким чином, ордината точки перетину прямих ОР_α і t дорівнює тангенсу числа α. Тому пряму t нази­вають віссю тангенсів.

Слайдер 6.

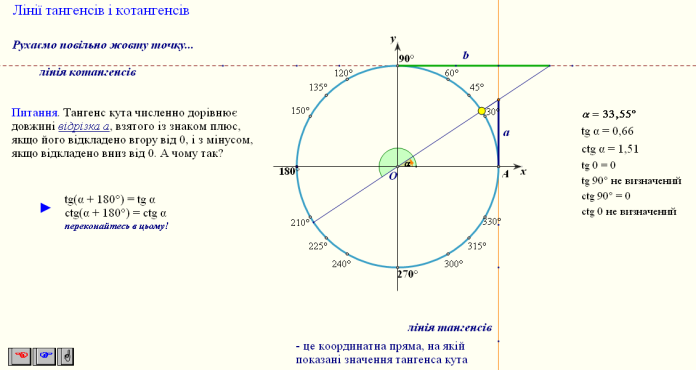
5. Означення котангенса. Лінія котангенсів.(Метод навчального тренінгу)

     

 Котангенсом числа α називається від­ношення косинуса числа α до його синуса:   .

Котангенс визначений для всіх α, крім таких значень, для яких sin α 0, тобто, a = π n, n Ζ.

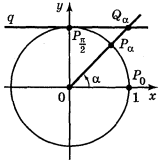
Введемо поняття лінії котангенсів (рис. ). Проведемо дотичну q до одиничного кола в точці . Для довільного числа α, якщо sin α 0 і відповідно точка Р_α (cos α, sin α) не лежить на осі ОХ і тому пряма ОР_α перетинає пряму q у деякій точці Q_α з ординатою, що дорівнює 1. Із трикутника ОQ_α  маємо: , звідси х = ctg α. Таким чином, абсциса точки перетину прямої ОР_α і q дорівнює котангенсу числа α, тому пряму q називають віссю котангенсів.

 

 

Слайдер 7.

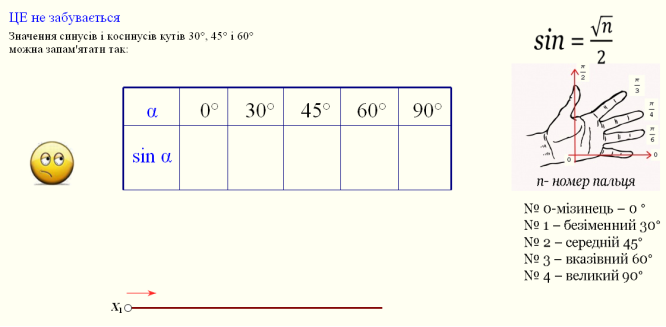. Слайдер 8.

 

 

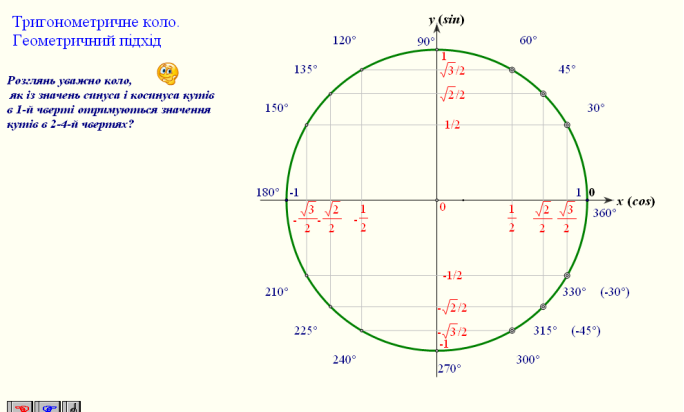
Слайдер 9.

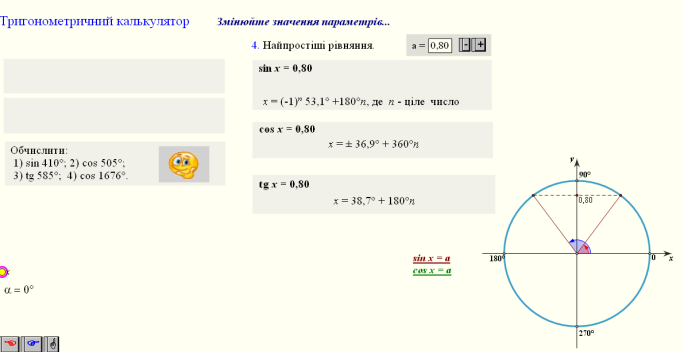
sin 405 = sin(360 + 45) =                               cos 480 = cos 120 =

tg 585 = tg 225 = 1                                                cos 1650 = cos 210 =

 

6. Знаки в чвертях.  Монотонність  синуса в чвертях:

I чверть – зростає від 0 до 1                                             II чверть  – спадає від 1до 0

III чверть – спадає від 0до (-1)                                        IV чверть– зростає від (-1) до 0

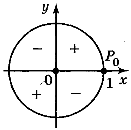
Знаки синуса в чвертях:

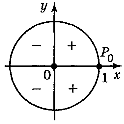
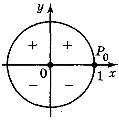
Монотонність  косинуса в чвертях:

I чверть  – спадає від 1 до 0             II чверть  – спадає від 0до (-1)

III чверть– зростає від (-1) до 0        IV чверть– зростає від 0 до 1

Знаки косинуса в чвертях:

Слайдер 10.

 

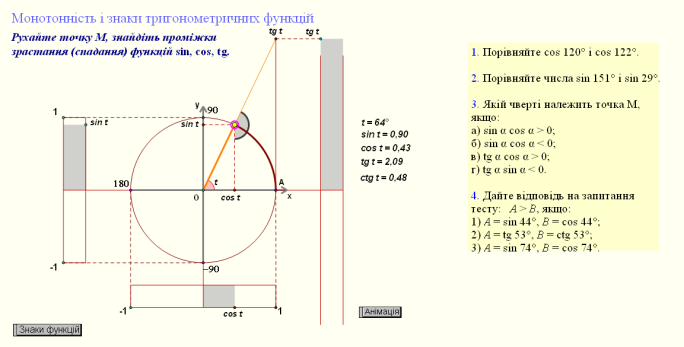
Тренувальні вправи відповіді:

№1. cos 120°   >  cos 122°.

№ 2. Порівняйте числа sin 151°  =  sin 29°.

 №3. Якій чверті належить Р_α, якщо:

а) sin α cos α > 0;   б) sin α cos α < 0;    в) tg α cos α > 0;    г) ctg α sin α < 0?

Відповідь: а) І або III; 6) II або IV; в) І або II; г) II або III.

№4. 4. Дайте відповідь на запитання тесту:   А > B, якщо:

1) A = sin 44°, B = cos 44°;

2) A = tg 53°, B = ctg 53°;

3) A = sin 74°, B = cos 74°.

Слайдер 11.

 

Учнівський проект«Тригонометрія в оточуючому нас світі та в житті людини».

Сильніші учні класу, за бажанням проходять комп’ютерний Тест.

 

Слайдер 12

4. Узагальнення та систематизація знань, умінь та навичок учнів.(Метод: аналіз узагальнюючої таблиці)

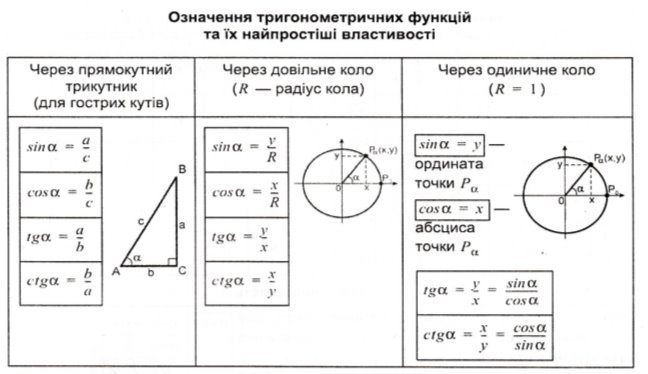
Запитання для контролю

1. Сформулюйте означення тригонометричних функцій гострого кута в прямокутному трикутнику.

2. Сформулюйте означення тригонометричних функцій довільного кута:

а) використовуючи коло радіуса R з центром у початку координат;

б) використовуючи одиничне коло.

 

5.Підведення підсумків урок.( рефлексія)

Учням  пропонується закінчити речення

1. Сьогодні я дізналась…
2. Було цікаво…
3. Було важко…
4. Я зрозумів, що…
5. Тепер я можу…
6. Я навчилась…
7. У мене вийшло…
8. Я зміг….
9. Мене здивувало…
10.  Урок дав мені для життя…

    Підводжу підсумки уроку,  відмічаю роботу учнів, коментую отримані оцінки  на уроці.

6. Домашнє завдання. 1. Вивчити конспект,  §10,

Компетентність висока № 405,408.

                            середня №  № 392,398, повт. №423.

                             низька «Виконаємо разом» №1,2,3  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Аналіз уроку

      Методична розробка уроку відповідає всім методичним вимогам  проведення занять виду  інтерактивної лекції  і складена у повній відповідності до програми з дисципліни  ”Математика”. В розробці відображено всі етапи уроку.  Проведена мотивація пізнавальної діяльності учнів, де використано: історико – довідниковий матеріал,  встановлено реальні міжпредметні зв’язки теми з іншими дисциплінами, які вивчаються в школі за допомогою методу логічної градації.

    Актуалізація опорних знань учнів проводиться за допомогою методу встановлення відповідностей, що пожвавлює роботу учнів на уроці і відповідає вимогам сучасності.  Для закріплення  матеріалу практикую інтерактивні форми роботи.

     Вивчення матеріалу проводиться послідовно із застосуванням інформаційно – комунікативних технологій. Кожен інформаційний модуль закріплюється в процесі уроку за допомогою влучних прикладів, конкретних вправ з теми. Матеріал теми перекликається з темами геометрії за неповну школу та базується  на матеріалі вивченому на попередніх уроках , тому учні мають можливість взяти участь у з’ясуванні деяких властивостей та теоретичних фактів.

     Узагальнення та систематизація знань та навиків учнів також має не одну форму: аналіз узагальнюючої таблиці, елементи ігрових технологій гра - сканворд.

    В методичній розробці висвітлено багато різноманітних форм та методів роботи:   навчальний тренінг,  інструктування,  доведення формул,  самостійна робота,  тренувальні вправи, бесіда, ілюстрація, пояснення,  метод проектів тощо.

    Методична розробка забезпечена всіма необхідними матеріалами візуального супроводження,  роздатковими матеріалами. Підготовлено презентацію уроку для  мультимедійного  проектора.

 

IY. Закріплення нового матеріалу.

 

Розв’язання завдань за картками біля дошки, використовуючи макет числового кола, на якому відмічені деякі кутові значення.

 

Варіант  1.

Частина 1.

1. Яке з даних чисел додатне? . . С.   .  .

2. Яке з даних чисел від’ємне? . . С. . .

3. Розкласти в порядку спадання числа: , , . .   . С. .  .

4. Розкласти числа , , в порядку зростання. . . С.   .    .

5. Яка нерівність неправильна? . . С. . .

6. Розкласти в порядку зростання числа , , . .  С. . .

7. Серед вказаних чисел знайти найбільше. . . С. . .

8. Розкласти в порядку спадання числа: x = tg 2550, y = sin 300, z = tg 1530. . . С. . .

9. Які з даних чисел , , , від’ємні? .   .     С.     .    . таких нема

10. Обчислити: . .   .     С.    .     .

11.  Обчислити .  0,2   . 0,30   С. 0,25    . 0,35   . 0,15

12. Обчислити . .    .    С.     .    .

13. Розв’язати рівняння . 8    .4    С. 2    . 16   . 1

14. Обчислити: . 0   .    С.    . -1    . 1

Частина 2.

1. Яке число додатне?        .  .  С.  .  .?

Чому дорівнює кут повороту, який показано на рисунку . 3600 .-4500  С. 4050 . 4500 .-4050

3. Розкласти числа , , в порядку їх   спадання. . . С.   . .

 

Відповіді варіанту 1:

Частина 1.									Частина 2.
1	С		6			11	С		1	С
2			7			12	С		2
3			8			13			3
4			9			14
5			10	С

 

Варіант  2.

Частина 1.

1. Яке з даних чисел додатне?   . . С. . .

2. Яке з даних чисел від’ємне?   . . С. . .

3. Розкласти в порядку зростання числа: , , , . .     .      С. .     .

4 Розкласти в порядку спадання числа , , . .     .      С. .           .

5. Яка різниця від’ємна? .    .    С.  .     .

6. Розкласти в порядку спадання числа , , z = ctg 9300.  . . С. .  .

7. Серед даних чисел знайти найбільше. .  . С. . .

8. Обчислити. tg 300 sin 600 ctg 2250. . 1,5    .0,5     С.    .     .

9. Розкласти в порядку спадання числа: , , , . .      .       С.  .     .

10. Обчислити: +. . 1    .-1    С.    .    .

11. Обчислити . .     .      С.-1     . 1     .

12. Обчислити значення .    .     С.     . 1    .

13. Розв’язати рівняння. .     .      С. 2     .      .

14. Дано числа , , , . Знайти добуток більшого із них на найменше. . -1,4   . -1,5    С.      . 1,5    .

Частина 2.

1.  Яке число додатне?        .  .  С.  .  .?

2. Чому дорівнює кут повороту, який показано на рисунку . . -2700 .-6300  С. 2700 .6300  .-450

3. Розкласти числа , , , , в порядку спадання. .    .     С.      .      .

 

Відповіді варіанту 2:

Частина 1.									Частина 2.
1	С		6			11	С		1
2			7			12			2
3			8			13			3
4	С		9			14
5			10

 

В індивідуальну карточку учень вписує своє прізвище та ім’я, а також букву з правильною відповіддю тесту.

 

Відповіді варіанту 1:

Частина 1.									Частина 2.
1	С		6			11	С		1	С
2			7			12	С		2
3			8			13			3
4			9			14
5			10	С

 

Відповіді варіанту 2:

Частина 1.									Частина 2.
1	С		6			11	С		1
2			7			12			2
3			8			13			3
4	С		9			14
5			10

Y Підведення підсумків. Самооцінювання.

Запитання для контролю

1. Сформулюйте означення тригонометричних функцій гострого кута в прямокутному трикутнику.

2. Сформулюйте означення тригонометричних функцій довільного кута:

а) використовуючи коло радіуса R з центром у початку координат;

б) використовуючи одиничне коло.

3. Що мають на увазі, коли говорять про синус, косинус, тангенс і котангенс

числа α?

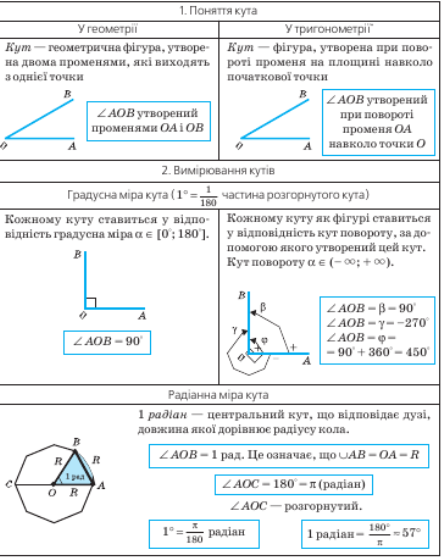
Домашнє завдання: №

Знайти значення , , и кутів із таблиці (наприклад: якщо в класі знаходили значення , то дома знайти  значення  , і кутів із таблиці).

Заповнити таблицю значень:

	7800	3150	1500	1800	-4500	0	-6300

 

Індивідуальна карточка учня:

Прізвище, ім’я ______________				Знаки тригонометричних функцій. Порівняння значень. Стандартні значення.
Частина 1.									Частина 2.
1			6			11			1
2			7			12			2
3			8			13			3
4			9			14			4
5			10

 

 

Індивідуальна карточка учня:

Прізвище, ім’я ______________				Знаки тригонометричних функцій. Порівняння значень. Стандартні значення.
Частина 1.									Частина 2.
1			6			11			1
2			7			12			2
3			8			13			3
4			9			14			4
5			10

 

 

Індивідуальна карточка учня:

Прізвище, ім’я ______________				Знаки тригонометричних функцій. Порівняння значень. Стандартні значення.
Частина 1.									Частина 2.
1			6			11			1
2			7			12			2
3			8			13			3
4			9			14			4
5			10

 

Індивідуальна карточка учня:

Прізвище, ім’я ______________				Знаки тригонометричних функцій. Порівняння значень. Стандартні значення.
Частина 1.									Частина 2.
1			6			11			1
2			7			12			2
3			8			13			3
4			9			14			4
5			10