УРОК 1

Тема уроку: Числові функції. Зростаючі і спадні, парні і непарні функції.

Мета уроку: Узагальнення і систематизація знань учнів про чис­лові функції (область визначення і область значення функцій, зростаючі і спадні функції, парні і непарні функції).

І. Мотивація навчання.

Процеси реального світу тісно пов'язані між. собою. Серед різноманіття явищ вчені виділили такі, у яких взаємозв'язок величин настільки тісний, що, знаючи значення однієї з них, можна визначити значення другої величини.

Наприклад, знаючи сторону квадрата, можна знайти його площу або периметр.

Залежність змінної у від змінної х, при якій кожному значенню χ відповідає єдине значення у, називається функцією.

З поняттям функції ви познайомилися в курсі алгебри. По­няття функції є важливим поняттям курсу алгебри і початків аналізу, отже, ми повинні згадати і узагальнити відомості про функції. Крім того, досліджуючи властивості функцій, ми має­мо можливості ґрунтовніше пізнати реальний світ.

II. Систематизація і узагальнення основних відомостей про числові функції.

Числовою функцією з областю визначення D називається за­лежність, при якій кожному числу х із множини D ставиться у відповідність по деякому правилу єдине число у із множини Е.

Змінна х називається незалежною змінною або аргументом функції, а змінна у — залежною змінною або функцією.

Функцію позначають латинськими буквами f, g, h... (або f(x), g(x), h(x)„.) або рівностями у = f(x), у = g(x), у = h(x)... Якщо задане конкретне значення незалежної змінної х = х₀, то у₀ = f(x₀) називається значенням функції f в точці х₀.

Область визначення функції позначається D(f) (від анг. defi­ne — визначити). Множина, яка складається із всіх чисел f(x) таких, що х належить області визначення функції f, називаєть­ся областю значень функції і позначається E(f) (від анг. exist — існувати).

Розглянемо приклад. Результати вимірювання температури тіла хворого в залежності від часу подано в таблиці:

Залежність у·= f(x) є функцією, х — незалежна змінна, у — залежна змінна.

f(9) = 39, f(12) = 38.5,..., f(24) = 37.

D(f) = {9;12;15; 18; 21; 24}.

E(f) = {39; 38,5; 38,3; 37,3; 37,1; 37}.

Функцію можна задати за допомогою таблиці, графіка, фор­мули.

Найчастіше функцію задають формулою, яка дає можливість одержати значення залежної змінної у, підставивши конкретне значення аргументу х.

Наприклад. Якщо кожному значенню х із множини дійсних чисел поставити у відповідність квадрат цього числа, то-функ­цію можна записати у вигляді формули: у = х² або f(x)= x².

Областю визначення функції у = f(x), яка задана формулою, називається множина тих значень, які може приймати х, тобто формула має зміст (усі дії, вказані формулою, можна виконати). При знаходженні області визначення слід пам'ятати:

1. Якщо функція є многочленом  у = а_n хⁿ + α_n-1 x^n-1 +... + α₁x + a₀,

то D(y) = (-; +) = R.

2) Якщо функція має вигляд у = , де f(x) і g(x) — многочлени, то слід вважати g(x)0 (знаменник дробу не дорів­нює 0).

3) Якщо функція має вигляд у = , то слід вважати f(x) > 0 (арифметичний квадратний корінь існує тільки з невід'ємних чисел).

Графіком функції у = f(x) називається множина всіх точок пло­щини з координатами (x;f(x)) , де перша координата «пробігає» всю область визначення функції у = f(x), а друга координата — це відповідні значення функції в точці х.

Виконання вправ

1. Знайдіть значення функції:

 a) f(x) = у точках 1; -1; 5;

б) f(x) = у точках 3; 12; 52.

Відповідь: а) f(1) = 2, f(-1) = 0; f(5) = 1,2;

б) f(3) = 0; f(12) = 3; f(52) = 7

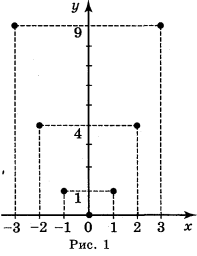
2. Функцію задано формулою у = x² на області визначення D = {-3; -2; -1; 0; 1; 2; 3}. Задайте її за до­помогою:

а)таблиці;        б)графіка.

Відповідь:

б) рис. 1

3. Знайдіть область визначення функції:

а) у = х² + х³; б) ; в) ; д) ; є) .

  Відповідь:

a) D(y) = R;  б) D(y) = (-; 3) (3; +);  в) D(y) = (-;-2) (-2;0) (0;+);

г) D(y) = (-; -3) (-3; 3) (3; +); д) D(y) = (-;l) (l;4) (4;+);

є) D(y) = [-6;+).

4. Знайдіть область значень функції: а) у =  ;      б) у = -1.

Відповідь: а) Е(у) = [2; +);     б) Е(у) = [1; +).

5. Для функцій, графіки яких зображено на рис. 2, вкажіть D(y) і Е(у).

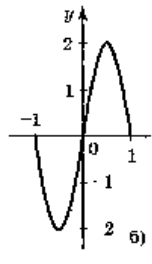
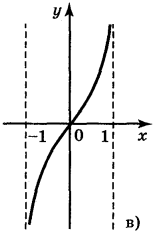
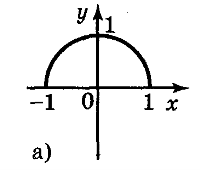
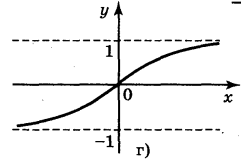
Рис. 2

Відповідь:

а) D(у) = [-1;1]; Е(у) = [0;1]; б) D(y) = [-1;1]; E(y) = [-2;2];

в) D(y) = (-1;1); E(у) = R;     г) D(y) = R; Е(у) = (-1;1).

6. Які із ліній, зображених на рисунку 3, є графіком функції? Чому?

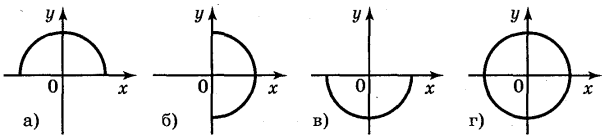
Відповідь: а); в).        

III. Систематизація і узагальнення знань учнів про спадні, зростаючі, парні та непарні функції.

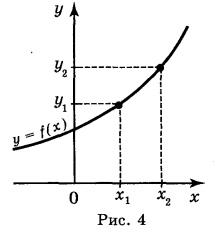
Функція у = f(x) називається зростаючою (рис. 4), якщо більшому значенню аргументу відповідає більше значення функції, тобто для будь-яких значень х₁ і х₂ з області визначення функції таких, що х₁ < х₂, виконується нерівність f(x₁) < f(x₂) і навпаки: із того, що f(x₁) < f(x₂) виконується нерівність х₁ < х₂.

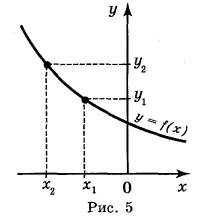
Функція у = f(x) називається спадною (рис. 5), якщо більшому значенню аргументу відповідає менше значення функції, тобто для будь-яких значень х₁ і х₂ з області визначення функції та­ких, що х₁ < х₂, виконується нерівність f(x₁) > f(x₂) і навпаки: якщо у = f(x) — спадна, то із того, що f(x₁) > f(x₂), виконується нерівність х₁ < х₂.

Виконання вправ.

1. Користуючись графіками функцій, зображених на рисунку 6, укажіть проміжки зростання і спадання функцій.

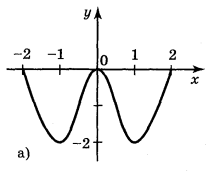
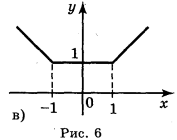
Відповідь:

а) на кожному з проміжків [-1;0], [1;2] функція зростає, на кожному з проміжків [-2;-1], [0;1] функція спадає;

б) на кожному з проміжків [-3;-2], [1;2] функція спадає; на проміжку [-2;1] функція зростає;

в) на проміжку (-;-1] функція спа­дає, на проміжку [-1; 1] функція постійна, на проміжку [1;+) функція зростає.

2. Функція у = f(x) зростаюча. Порівняйте:

а) f(10) і f(-10);    б) і .

Відповідь:         а) f(10) > f(-10);    б) < .       

3. Функція у = f(x) — спадна на R. Порівняйте:

а) f(10) і f(-10);    б) і .

Відповідь: а) f(10) < f(-10);    б) > .

4. Знайдіть проміжки зростання і спадання функції:

а) у = x - 3;        б) у = -x + 3;   в) у = x² + 1;       г) у = -х² + 1.

Відповідь:

а) зростає на R;  б) спадає на R;

в) зростає на проміжку [0;+) і спадає на проміжку (-;0];

г) зростає на проміжку (-;0] і спадає на проміжку [0;+).

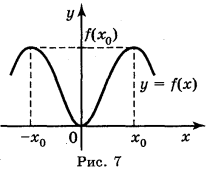Функція у = f(x) називається парною, якщо для будь-якого значення х із D(y) значення – х також належить D(y) і виконується рівність f(-x) = f(x).

Графік парної функції симетричний відносно осі ОУ (рис. 7).

Приклад 1. Чи парна функція f(x) = χ⁴ + χ² ?

Оскільки D(f) = R і f(-x) = (-х)⁴ + (-x)² = х⁴ + х² = f(x) , функція парна.

Приклад 2. Чи парна функція f(x) = х² + х ?

Оскільки D(f) = R, але f(-x) = (-х)² + (-х) = х² – х f(x), то функція не є парною.

Функція у = f(x) називається непарною, якщо для будь-якого значення х із D(y) значення -х D(y) і виконується рівність f(-x) = -f(х).

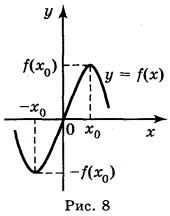
Графік непарної функції симет­ричний відносно початку координат (рис. 8).

Приклад 3. Чи непарна функція f(х) = x³ - x⁵?

Оскільки D(f) = R і f(-х) = (-х)³ - (-х) =  -х³ + х⁵ =

= -(х³ - х⁵) = -f(х), функція непарна.

Приклад 4. Чи непарна функція f(х) = х³ – х² ?

Оскільки D(f) = R і f(-x) = (-х)³ - (-х)² = -х³ - х² = -(х³ + х²)f(x) = -х³ + х², функція не є непарною.

Виконання вправ

1. Які із функцій, графіки яких показано на рисунку 9, є пар­ними, а які непарними?

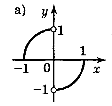
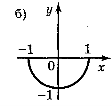
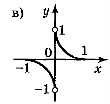
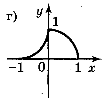
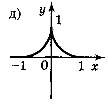
Рис. 9

Відповідь: непарні — а), в);    парні — б) д).

2. Які із поданих функцій а) у = х³ + 2х⁷; б) у = ; в) у = ;

г) у = 3x² + х⁶; д) у = х +1; є) у = +1 є парними, а які — не­парними? Відповідь: парні — в), г); е);   непарні — а).

IV. Підведення підсумків уроку.

V. Домашнє завдання.

Розділ І § 1(1). Запитання і завдання для повторення розділу І № 1-12. Вправи № 1 (2; 5; 7), № 2 (3; 5).