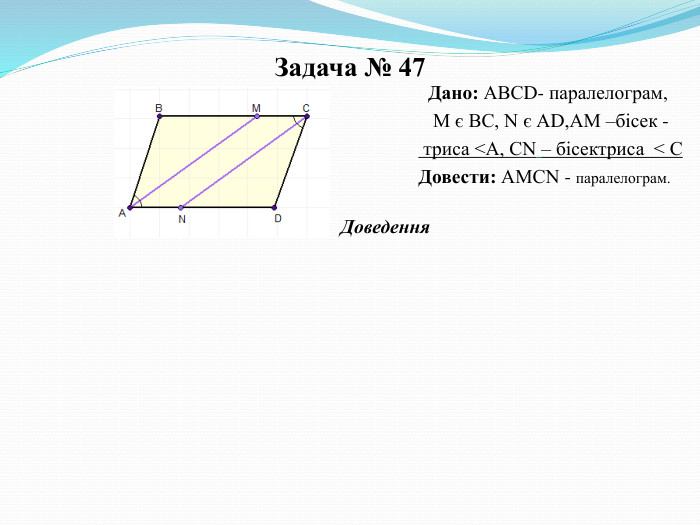
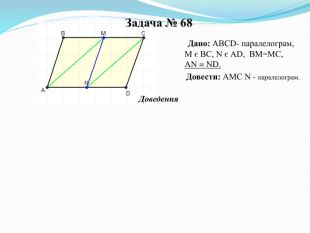
ОЗНАКИ ПАРАЛЕЛОГРАМА
Про матеріал
Мета: засвоїти ознаки паралелограма; сформувати вміння відтворювати вивчені ознаки, а також використовувати їх разом із вивченими раніше властивостями для розв’язування задач на доведення та обчислення Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку