ОЗНАКИ РІВНОСТІ ПРЯМОКУТНИКІВ

Точка і пряма. Властивості точок і прямих. Промінь22.04.2023 Ознаки рівності прямокутних трикутників. Розв’язування типових вправ22.04.2023 Геометрія

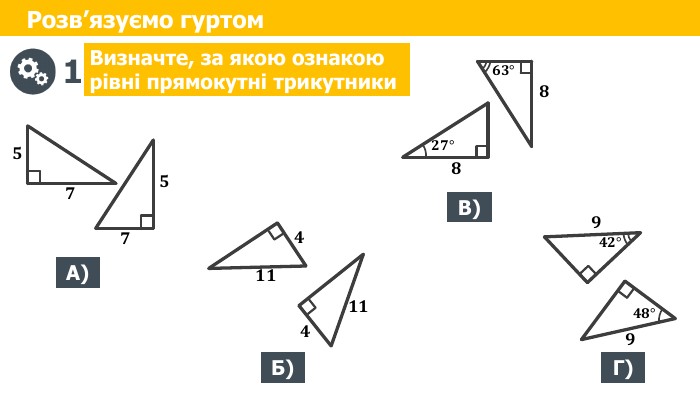
Відповідаємо. Який трикутник називається прямокутним?Яка сторона прямокутного трикутника називається гіпотенузою?Які сторони прямокутного трикутника називаються катетами?Чому сума гострих кутів прямокутного трикутника дорівнює 𝟗𝟎°? Чому гіпотенуза прямокутного трикутника більша за будь-який з його катетів?Чому дорівнює катет прямокутного трикутника, що лежить проти кута 𝟑𝟎°? fillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.on

Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету і прилеглому до нього куту іншого, то такі трикутники рівніЯкщо катети одного прямокутного трикутника відповідно дорівнюють катетам іншого, то такі трикутники рівні1 Ознаки рівності прямокутних трикутників. Пригадайте першу ознаку рівності трикутників1 Пригадайте другу ознаку рівності трикутників22 Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету і прилеглому до нього куту іншого, то такі трикутники рівніДоведіть усно цю ознаку. Якщо катети одного прямокутного трикутника відповідно дорівнюють катетам іншого, то такі трикутники рівні

Якщо катет і протилежний йому кут одного прямокутного трикутника відповідно дорівнюють катету і протилежному йому куту іншого, то такі трикутники рівніЯкщо гіпотенуза і гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі й гострому куту іншого, то такі трикутники рівніЯкщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету і прилеглому до нього куту іншого, то такі трикутники рівніЯкщо катети одного прямокутного трикутника відповідно дорівнюють катетам іншого, то такі трикутники рівні1 Ознаки рівності прямокутних трикутників. Поясніть, чому коли у двох прямокутних трикутників є одна пара рівних між собою гострих кутів, то й інша пара гострих кутів – також рівні між собою кути?2 Доведіть усно цю ознаку33 Якщо гіпотенуза і гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі й гострому куту іншого, то такі трикутники рівні44 Якщо катет і протилежний йому кут одного прямокутного трикутника відповідно дорівнюють катету і протилежному йому куту іншого, то такі трикутники рівні

Ознаки рівності прямокутних трикутників. Теорема (Ознака рівності прямокутних трикутників за катетом і гіпотенузою)Теорема (Ознака рівності прямокутних трикутників за катетом і гіпотенузою)Якщо катет і гіпотенуза одного прямокутного трикутника дорівнюють відповідно катету і гіпотенузі іншого, то такі трикутники рівні

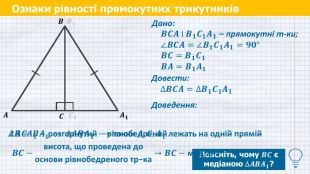
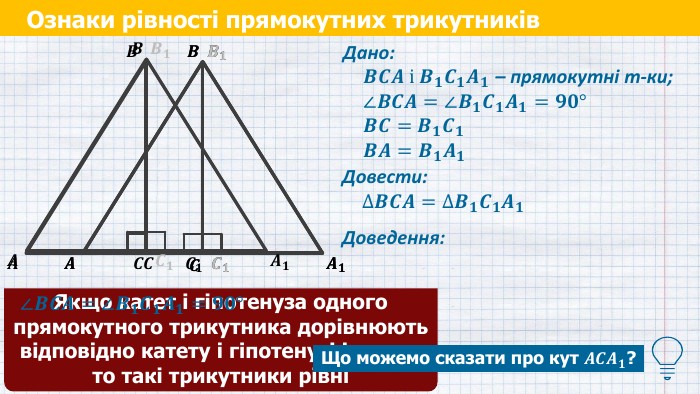
Ознаки рівності прямокутних трикутників. Теорема (Ознака рівності прямокутних трикутників за катетом і гіпотенузою)Якщо катет і гіпотенуза одного прямокутного трикутника дорівнюють відповідно катету і гіпотенузі іншого, то такі трикутники рівніЯкщо катет і гіпотенуза одного прямокутного трикутника дорівнюють відповідно катету і гіпотенузі іншого, то такі трикутники рівні𝑨 𝑪 𝑩 𝑨𝟏 𝑩𝟏 𝑪𝟏 Дано:𝑩𝑪𝑨 і 𝑩𝟏𝑪𝟏𝑨𝟏 – прямокутні т-ки;∠𝑩𝑪𝑨=∠𝑩𝟏𝑪𝟏𝑨𝟏=𝟗𝟎°𝑩𝑪=𝑩𝟏𝑪𝟏𝑩𝑨=𝑩𝟏𝑨𝟏 Довести:∆𝑩𝑪𝑨=∆𝑩𝟏𝑪𝟏𝑨𝟏 

Ознаки рівності прямокутних трикутників. Якщо катет і гіпотенуза одного прямокутного трикутника дорівнюють відповідно катету і гіпотенузі іншого, то такі трикутники рівні𝑨 𝑪 𝑩 𝑨𝟏 𝑩𝟏 𝑪𝟏 Доведення:𝑪𝟏 𝑪 𝑩 𝑨 𝑨𝟏 𝑩𝟏 𝑪𝟏 𝑪 𝑩 𝑨 𝑨𝟏 𝑩𝟏 𝑪𝟏 𝑪 𝑩 𝑨 ∠𝑩𝑪𝑨=∠𝑩𝟏𝑪𝟏𝑨𝟏=𝟗𝟎° Дано:𝑩𝑪𝑨 і 𝑩𝟏𝑪𝟏𝑨𝟏 – прямокутні т-ки;∠𝑩𝑪𝑨=∠𝑩𝟏𝑪𝟏𝑨𝟏=𝟗𝟎°𝑩𝑪=𝑩𝟏𝑪𝟏𝑩𝑨=𝑩𝟏𝑨𝟏 Довести:∆𝑩𝑪𝑨=∆𝑩𝟏𝑪𝟏𝑨𝟏 Що можемо сказати про кут 𝑨𝑪𝑨𝟏? style.colorstyle.color

Ознаки рівності прямокутних трикутників. Доведення:𝑨𝟏 𝑩𝟏 𝑪𝟏 𝑪 𝑩 𝑨 ∠𝑩𝑪𝑨=∠𝑩𝟏𝑪𝟏𝑨𝟏=𝟗𝟎° Дано:𝑩𝑪𝑨 і 𝑩𝟏𝑪𝟏𝑨𝟏 – прямокутні т-ки;∠𝑩𝑪𝑨=∠𝑩𝟏𝑪𝟏𝑨𝟏=𝟗𝟎°𝑩𝑪=𝑩𝟏𝑪𝟏𝑩𝑨=𝑩𝟏𝑨𝟏 Довести:∆𝑩𝑪𝑨=∆𝑩𝟏𝑪𝟏𝑨𝟏 Що можемо сказати про кут 𝑨𝑪𝑨𝟏? →∠𝑨𝑪𝑨𝟏−розгорнутий Що можемо сказати про точки 𝑨, 𝑪 і 𝑨𝟏? ∠𝑨𝑪𝑨𝟏−розгорнутий ∠𝑨𝑪𝑨𝟏−розгорнутий →точки 𝑨,𝑪, 𝑨𝟏 лежать на одній прямій 

Ознаки рівності прямокутних трикутників. Доведення:𝑨𝟏 𝑩𝟏 𝑪𝟏 𝑪 𝑩 𝑨 Дано:𝑩𝑪𝑨 і 𝑩𝟏𝑪𝟏𝑨𝟏 – прямокутні т-ки;∠𝑩𝑪𝑨=∠𝑩𝟏𝑪𝟏𝑨𝟏=𝟗𝟎°𝑩𝑪=𝑩𝟏𝑪𝟏𝑩𝑨=𝑩𝟏𝑨𝟏 Довести:∆𝑩𝑪𝑨=∆𝑩𝟏𝑪𝟏𝑨𝟏 Поясніть, чому ∆𝑨𝑩𝑨𝟏 рівнобедрений? ∠𝑨𝑪𝑨𝟏−розгорнутий →точки 𝑨,𝑪, 𝑨𝟏 лежать на одній прямій 𝑨𝑩=𝑩𝑨𝟏 → ∆𝑨𝑩𝑨𝟏 −рівнобедрений Поясніть, чому 𝑩𝑪 є медіаною ∆𝑨𝑩𝑨𝟏? 𝑩𝑪−висота, що проведена дооснови рівнобедреного тр−ка→𝑩𝑪−медіана 

Ознаки рівності прямокутних трикутників. Доведення:𝑨𝟏 𝑩𝟏 𝑪𝟏 𝑪 𝑩 𝑨 Дано:𝑩𝑪𝑨 і 𝑩𝟏𝑪𝟏𝑨𝟏 – прямокутні т-ки;∠𝑩𝑪𝑨=∠𝑩𝟏𝑪𝟏𝑨𝟏=𝟗𝟎°𝑩𝑪=𝑩𝟏𝑪𝟏𝑩𝑨=𝑩𝟏𝑨𝟏 Довести:∆𝑩𝑪𝑨=∆𝑩𝟏𝑪𝟏𝑨𝟏 𝑨𝑩=𝑩𝑨𝟏 → ∆𝑨𝑩𝑨𝟏 −рівнобедрений 𝑩𝑪−висота, що проведена дооснови рівнобедреного тр−ка→𝑩𝑪−медіана 𝑩𝑪−медіана 𝑩𝑪−медіана →𝑨𝑪=𝑪𝑨𝟏 𝑨𝑪=𝑪𝑨𝟏 𝑨𝑪=𝑪𝑨𝟏 𝑩𝑨=𝑩𝟏𝑨𝟏 𝑩𝑪−спільна сторона ∆𝑩𝑪𝑨=∆𝑩𝟏𝑪𝟏𝑨𝟏 (за третьою ознакоюрівності тр−в) Доведено

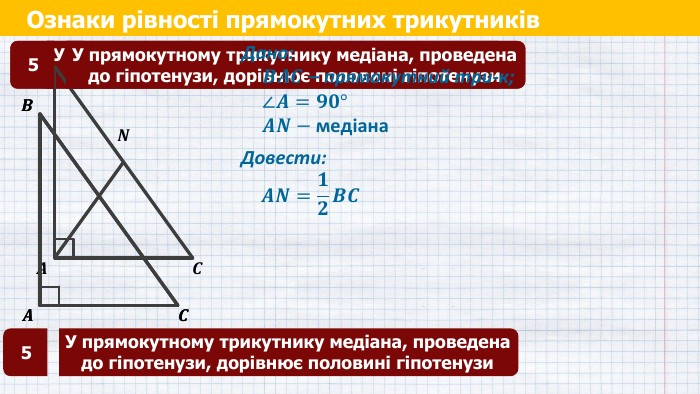
У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи5 Ознаки рівності прямокутних трикутників5 У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи𝑨 𝑪 𝑩 𝑨 𝑪 𝑩 𝑨 𝑪 𝑩 У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи5 У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи5 Дано:𝑩𝑨𝑪 – прямокутний три-к;∠𝑨=𝟗𝟎°𝑨𝑵−медіана Довести:𝑨𝑵=𝟏𝟐𝑩𝑪 𝑵 

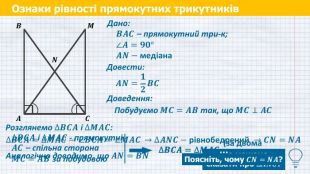
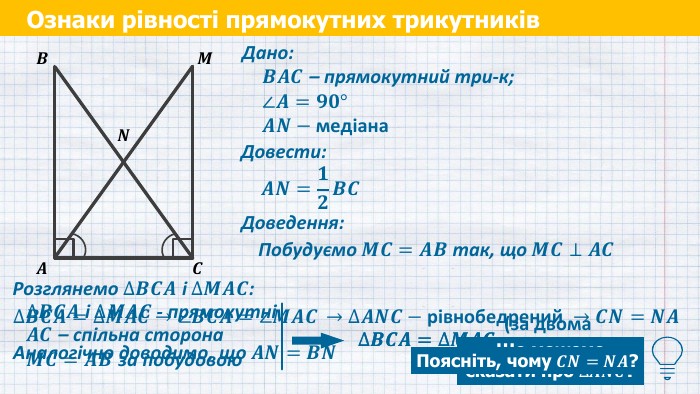
Ознаки рівності прямокутних трикутників𝑨 𝑪 𝑩 У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи5 Дано:𝑩𝑨𝑪 – прямокутний три-к;∠𝑨=𝟗𝟎°𝑨𝑵−медіана Довести:𝑨𝑵=𝟏𝟐𝑩𝑪 Доведення:𝑴 𝑵 Побудуємо 𝑴𝑪=𝑨𝑩 так, що 𝑴𝑪⊥𝑨𝑪 Розглянемо ∆𝑩𝑪𝑨 і ∆𝑴𝑨𝑪: ∆𝑩𝑪𝑨 і ∆𝑴𝑨𝑪 - прямокутні 𝑨𝑪 – спільна сторона 𝑴𝑪=𝑨𝑩 за побудовою ∆𝑩𝑪𝑨=∆𝑴𝑨𝑪 (за двомакатетами) Який можемо зробити висновок?

Ознаки рівності прямокутних трикутників𝑨 𝑪 𝑩 Дано:𝑩𝑨𝑪 – прямокутний три-к;∠𝑨=𝟗𝟎°𝑨𝑵−медіана Довести:𝑨𝑵=𝟏𝟐𝑩𝑪 Доведення:𝑴 𝑵 Побудуємо 𝑴𝑪=𝑨𝑩 так, що 𝑴𝑪⊥𝑨𝑪 Розглянемо ∆𝑩𝑪𝑨 і ∆𝑴𝑨𝑪: ∆𝑩𝑪𝑨 і ∆𝑴𝑨𝑪 - прямокутні 𝑨𝑪 – спільна сторона 𝑴𝑪=𝑨𝑩 за побудовою ∆𝑩𝑪𝑨=∆𝑴𝑨𝑪 (за двомакатетами) ∆𝑩𝑪𝑨=∆𝑴𝑨𝑪 ∆𝑩𝑪𝑨=∆𝑴𝑨𝑪 →∠𝑩𝑪𝑨=∠𝑴𝑨𝑪 →∆𝑨𝑵𝑪−рівнобедрений →𝑪𝑵=𝑵𝑨 Що можемо сказати про ∆𝑨𝑵𝑪? Поясніть, чому 𝑪𝑵=𝑵𝑨? Аналогічно доводимо, що 𝑨𝑵=𝑩𝑵 

Ознаки рівності прямокутних трикутників𝑨 𝑪 𝑩 Дано:𝑩𝑨𝑪 – прямокутний три-к;∠𝑨=𝟗𝟎°𝑨𝑵−медіана Довести:𝑨𝑵=𝟏𝟐𝑩𝑪 Доведення:𝑴 𝑵 ∆𝑩𝑪𝑨=∆𝑴𝑨𝑪 →∠𝑩𝑪𝑨=∠𝑴𝑨𝑪 →∆𝑨𝑵𝑪−рівнобедрений →𝑪𝑵=𝑵𝑨 Аналогічно доводимо, що 𝑨𝑵=𝑩𝑵 𝑪𝑵=𝑵𝑨 𝑨𝑵=𝑩𝑵 𝑪𝑵=𝑵𝑨 𝑨𝑵=𝑩𝑵 𝑪𝑵=𝑵𝑨=𝑩𝑵 →𝑨𝑵−медіана →𝑨𝑵=𝟏𝟐𝑩𝑪 Доведено

Розв’язуємо гуртом1𝟓 𝟕 𝟓 𝟕 А)𝟒 𝟏𝟏 𝟏𝟏 𝟒 Б)𝟐𝟕° 𝟖 𝟔𝟑° 𝟖 В)𝟒𝟐° 𝟗 𝟗 𝟒𝟖° Г)Визначте, за якою ознакою рівні прямокутні трикутники

Розв’язуємо гуртом2 На рисунку 𝑨𝑩⊥𝑨𝑪, 𝑴𝑵⊥𝑪𝑴, 𝑩𝑪=𝑪𝑵. Доведіть, що ∆𝑨𝑩𝑪=∆𝑴𝑵𝑪 𝑨 𝑩 𝑪 𝑴 𝑵 

Розв’язуємо гуртом3 Доведіть, що точка, яка лежить у внутрішній області кута і рівновіддалена від його сторін, належить бісектрисі цього кута𝑴 𝑵 𝑽 𝑶 

Розв’язуємо гуртом4 Кут між висотою прямокутного трикутника, проведеною до гіпотенузи, і одним з катетів дорівнює 𝟒𝟒°. Знайдіть гострі кути трикутника 𝑨 𝑩 𝑪 𝟒𝟒° 𝑫 

Розв’язуємо гуртом5 Доведіть, що два рівнобедрених трикутники рівні, якщо відповідно рівні їх бічні сторони і висоти, проведені до основ.𝑨 𝑩 𝑪 𝑴 𝑵 𝑽 𝑳 𝑲 

Розв’язуємо гуртом6 У прямокутному трикутнику один з кутів дорівнює 𝟔𝟎°, а сума гіпотенузи і меншого катета – 30 см. Знайдіть довжину гіпотенузи та медіани, що проведена до неї. 𝑨 𝑩 𝑪 𝟔𝟎° 𝑴 

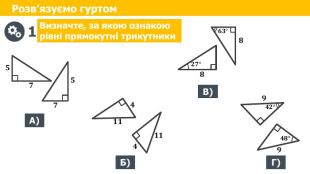
Відповідаємо. Сформулюйте ознаку рівності прямокутних трикутників за двома катетами. Сформулюйте ознаку рівності прямокутних трикутників за катетом і прилеглим до нього гострим кутом. Сформулюйте ознаку рівності прямокутних трикутників за гіпотенузою і гострим кутом. Сформулюйте ознаку рівності прямокутних трикутників за катетом і протилежним йому кутом. Сформулюйте ознаку рівності прямокутних трикутників за катетом і гіпотенузою. Яку властивість має медіана, що проведена до гіпотенузи прямокутного трикутника?fillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.on

Точка і пряма. Властивості точок і прямих. Промінь22.04.2023 Опрацювати §19 (ст. 109-110)Виконати № 468, 478, 485 Домашнє завдання. Бажаю творчих успіхів!22.04.2023