Презентація " Поняття вектора"
Про матеріал
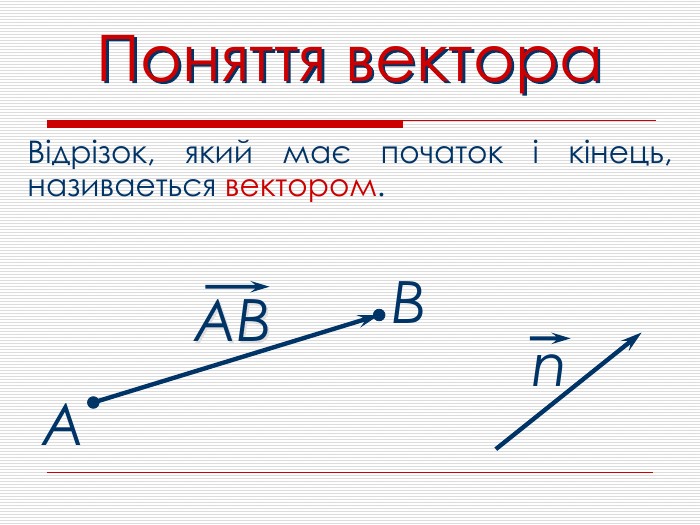
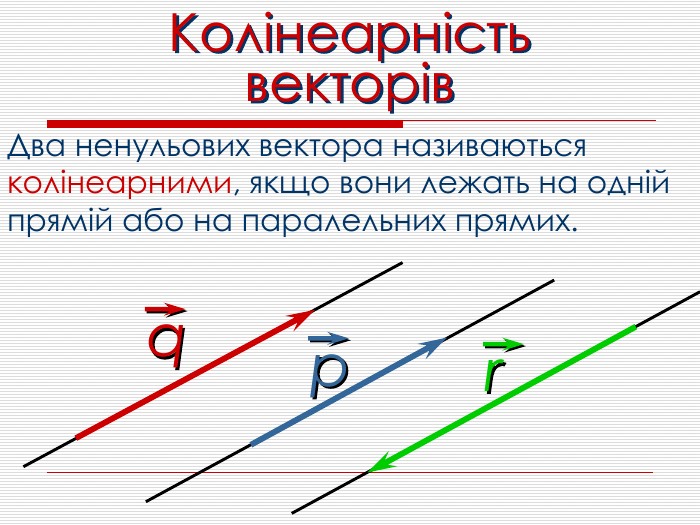
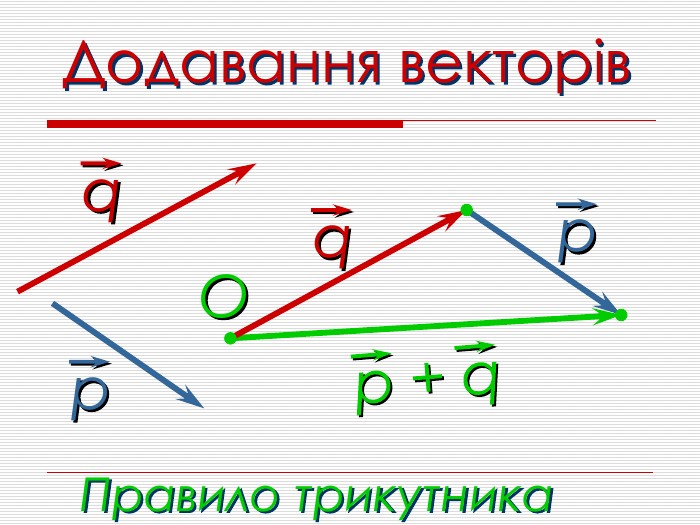
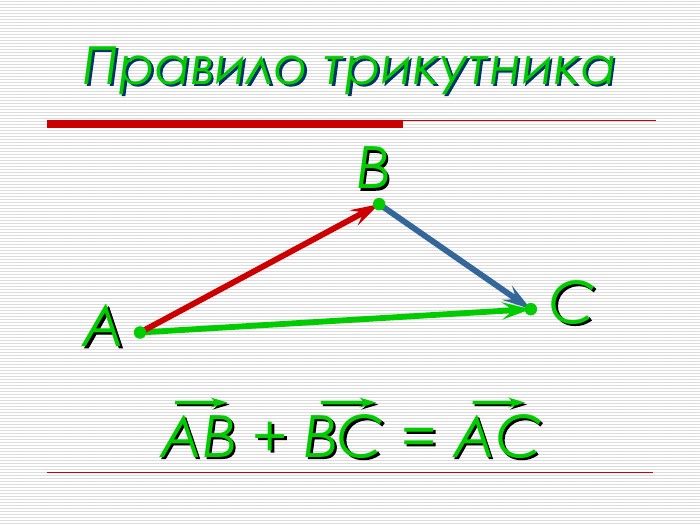
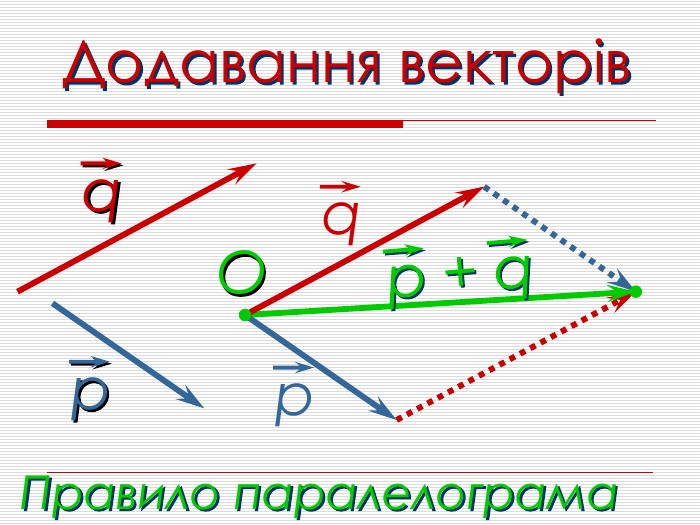
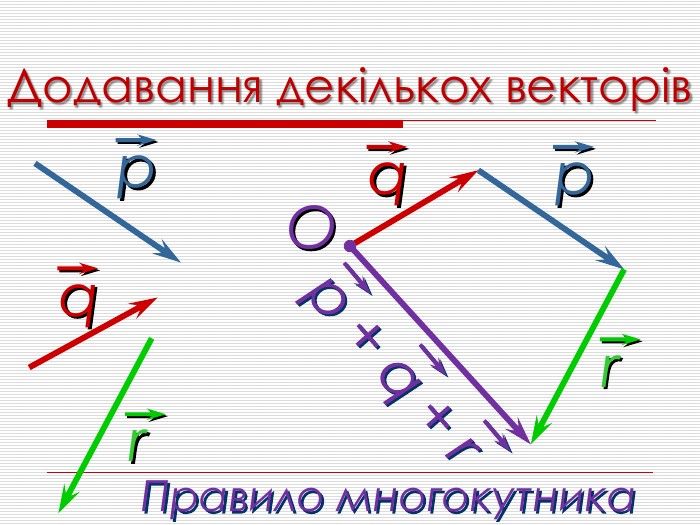
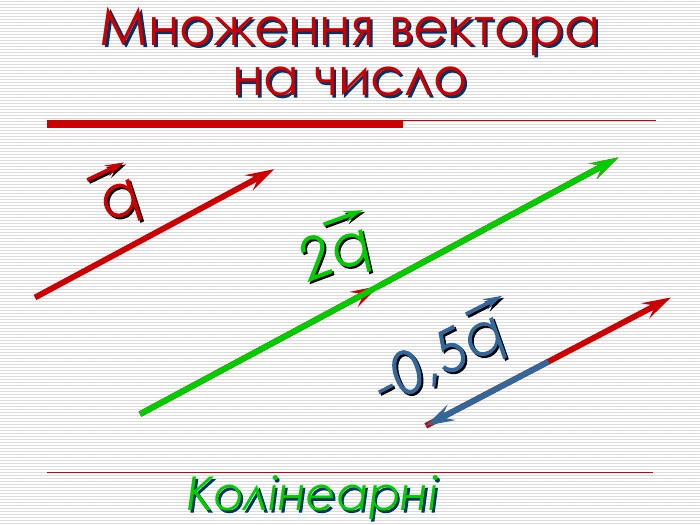
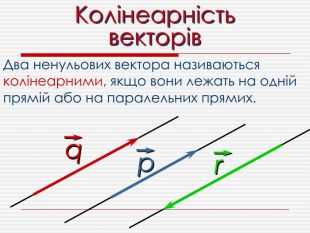
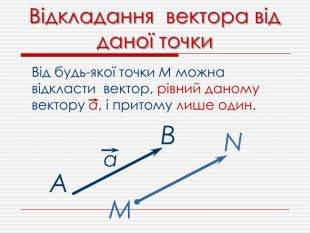
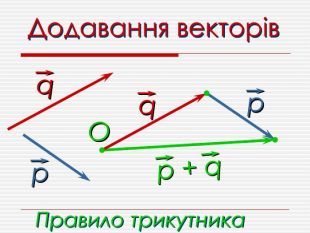
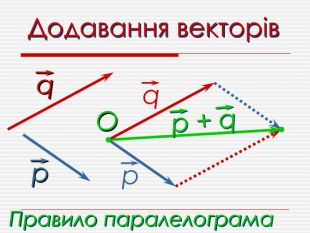
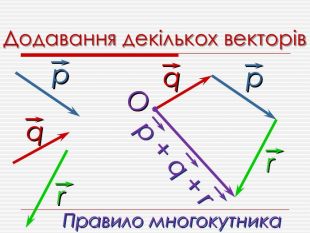
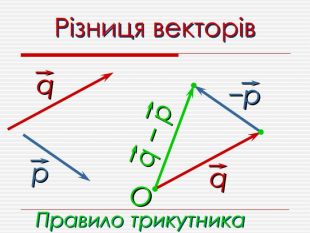
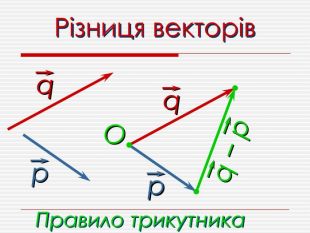
Анімована презентація для ознайомлення учнів з основними поняттями вектора, дій над векторами (додавання, віднімання, множення на число). Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку