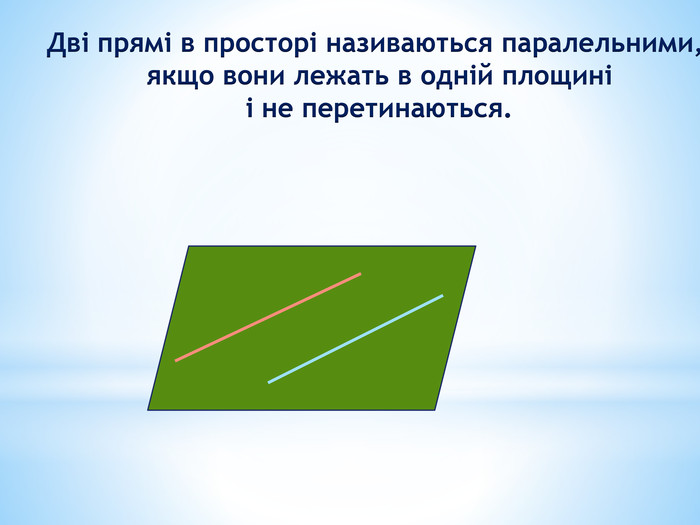
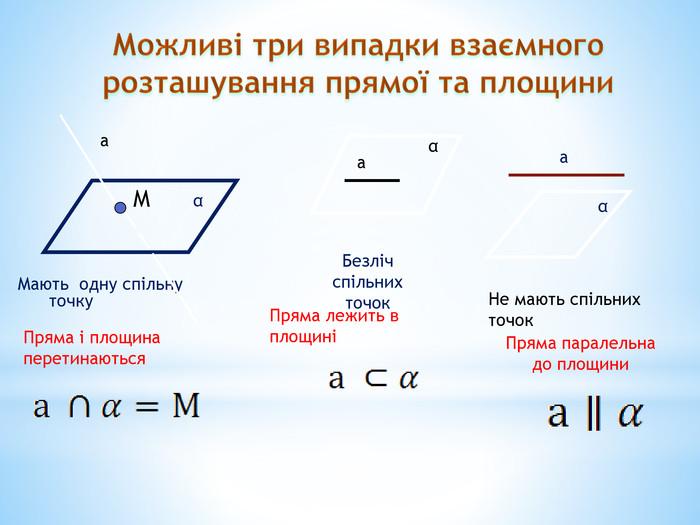
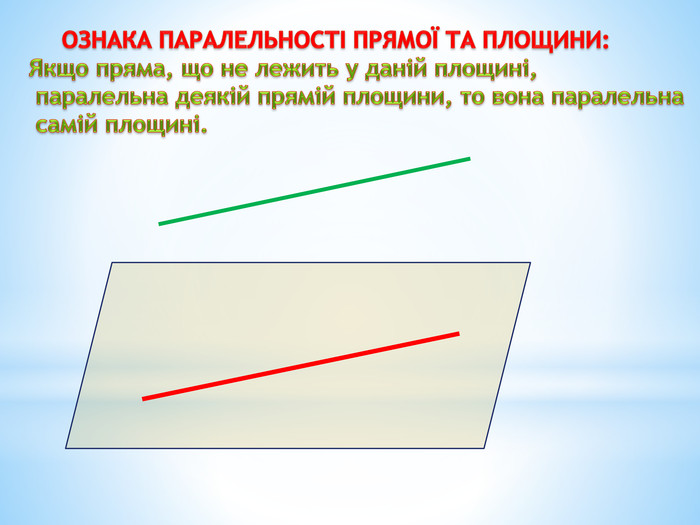
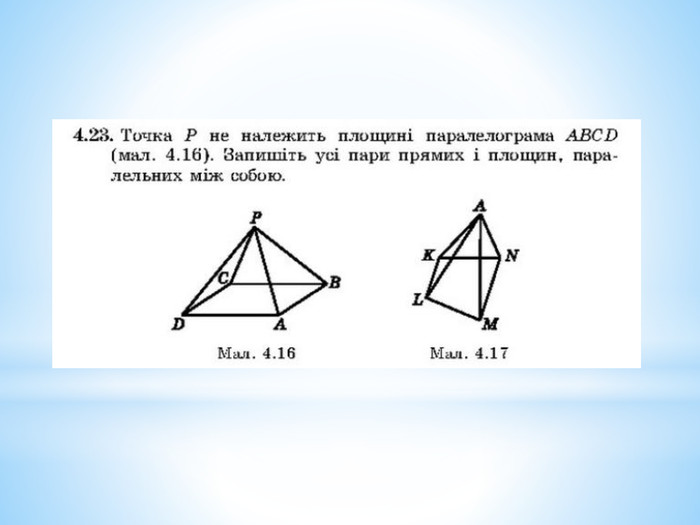
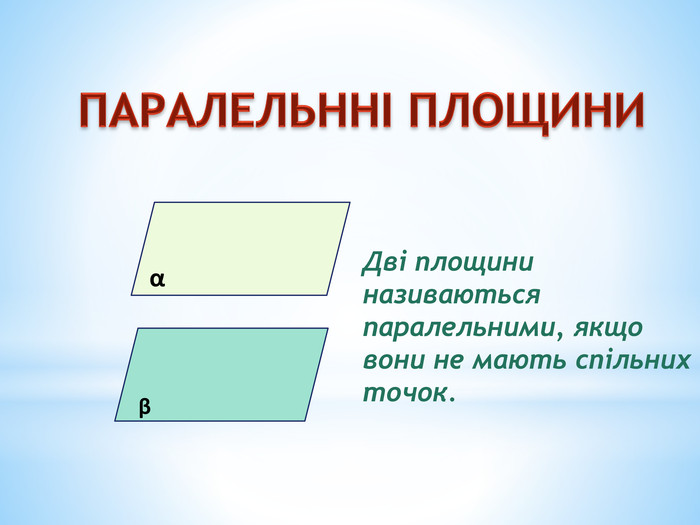
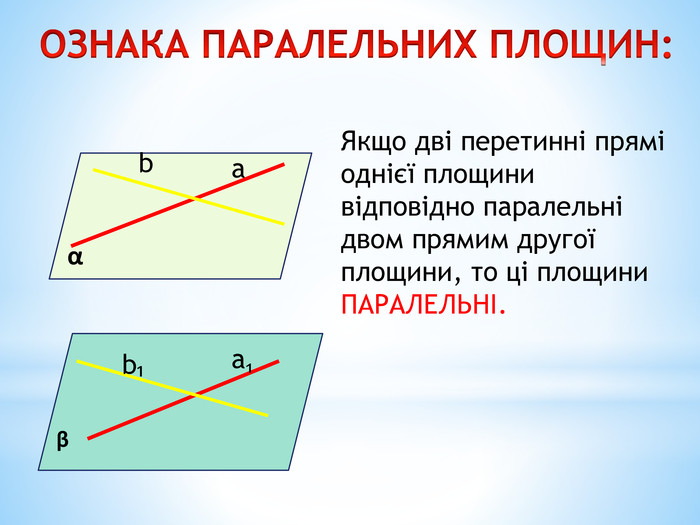
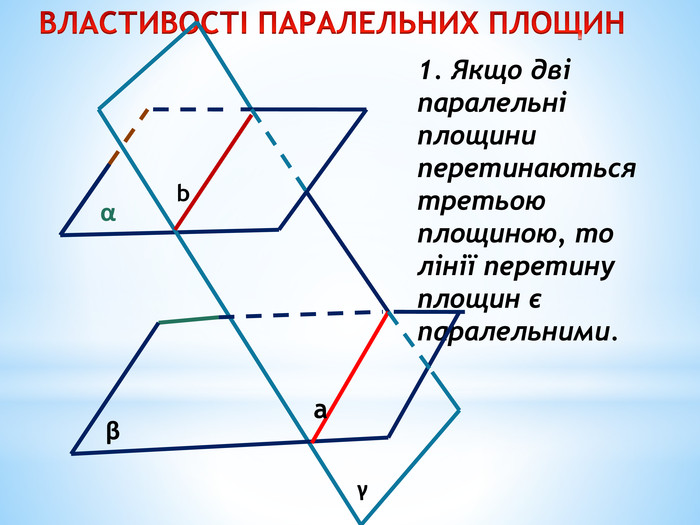
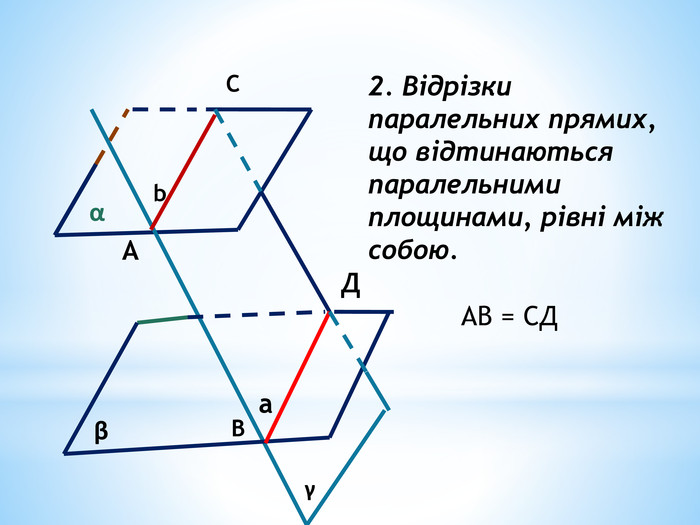
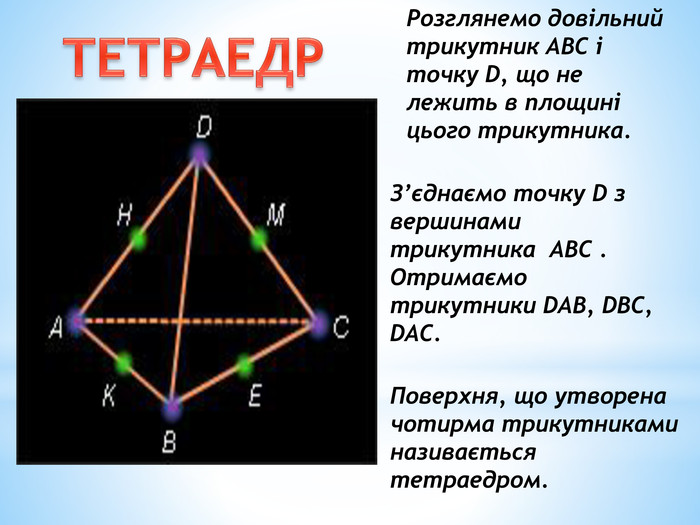
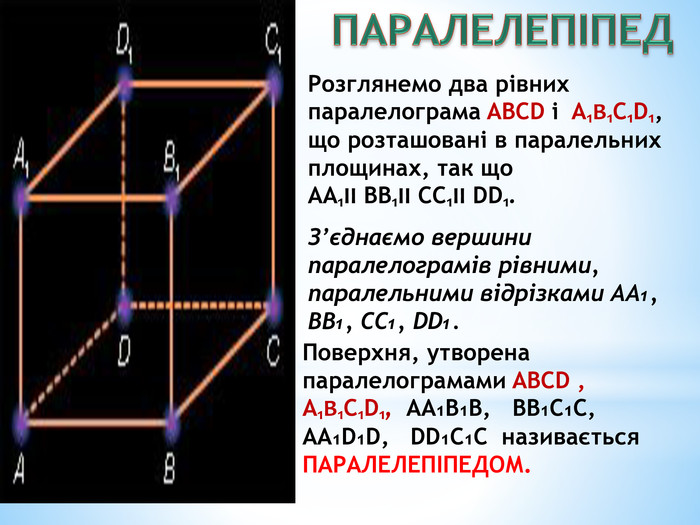
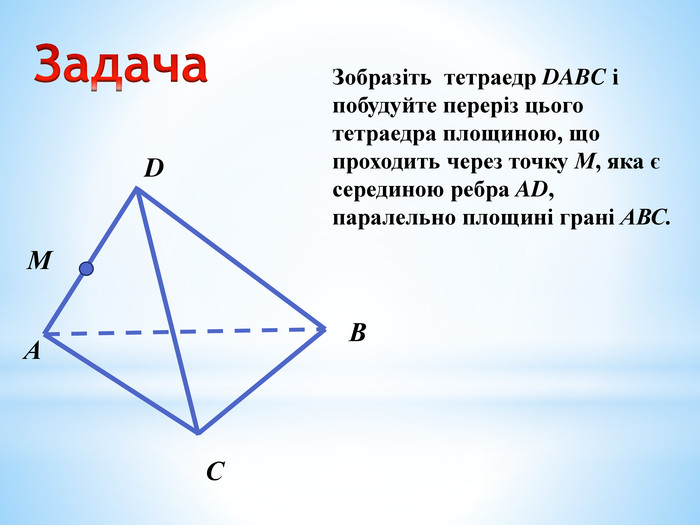
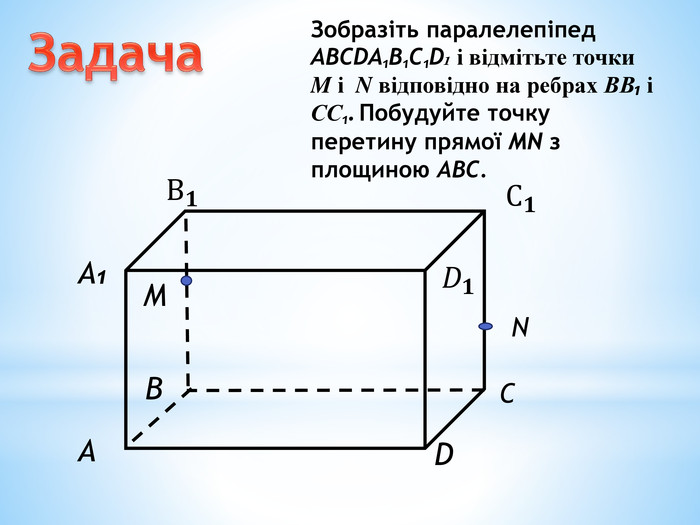
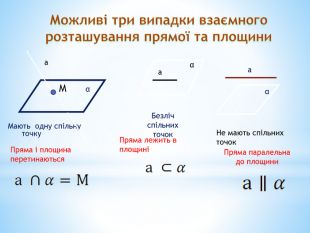
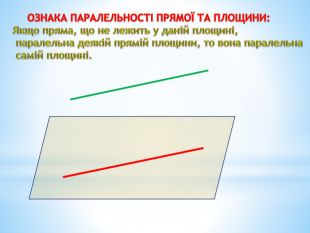
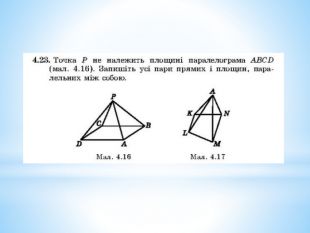
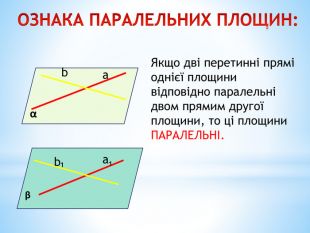
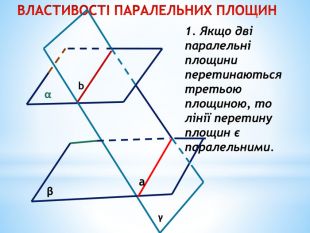
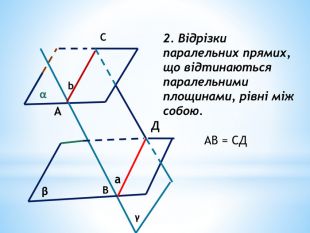
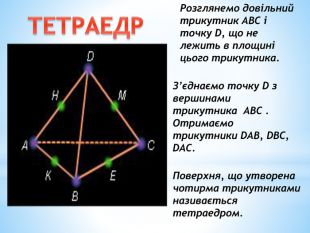
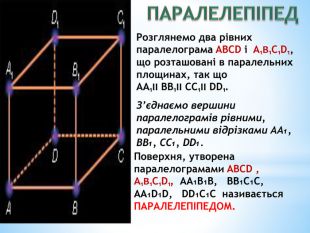
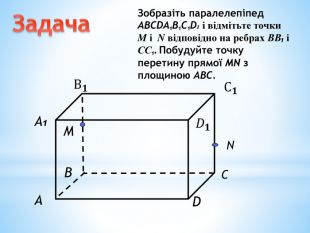
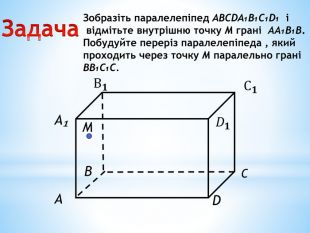
Паралельність прямої та площини.
Про матеріал
Презентація містить матеріали для повторення, вивчення нового та різноманітні завдання та приклади. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку