Педагогічні прийоми ефективного формування мотивів навчальної діяльності учнів на уроках математики (з досвіду роботи)

Педагогічні прийоми ефективного формування мотивів навчальної діяльності учнів на уроках математики (з досвіду роботи)

 

Умовою успіху в формуванні мотивів навчальної діяльності є висока пізнавальна активність учнів. Ефективне засвоєння знань передбачає таку організацію пізнавальної діяльності учнів, за якої навчальний матеріал стає предметом активних розумових і практичних дій. Пошуки методів навчання, що підсилювали б активізацію процесу навчання, призводять до підвищення актуальності розвивальних і проблемних методів самостійної роботи, творчих завдань. При цьому педагогічно обґрунтованою видається така організація навчання, за якої учні вчаться не з примусу, а за бажанням і внутрішніми потребами.

Учень на уроці повинен бути підготовлений до ефективного процесу пізнання, мати в ньому особисту зацікавленість, розуміти, що й навіщо він виконуватиме. Без виникнення цих мотивів навчання, без мотивації навчальної діяльності пізнання не може принести позитивного результату. З метою досягнення необхідного результату на уроках математики можна використовувати різноманітні прийоми формування мотивів навчальної діяльності. Розглянемо їх.

Особливо ефективним засобом для мотивації учнів на уроці є створення проблемної ситуації. Створювати проблемні ситуації допомагають задачі та запитання. При створенні проблемної ситуації ми виховуємо в учнів:

• вольову сферу: рішучість, самостійність, цілеспрямованість, сміливість, витримку, внутрішній план дій;
• мотиваційну сферу: пізнавальні мотиви, мотив самоосвіти, позитивне відношення до праці, необхідність в отриманні знань, умінь і навичок;
• основні прийоми розумової діяльності: спостереження, порівняння, аналіз, синтез, узагальнення, інтегрування, систематизації, індуктивних та дедуктивних міркувань, уміння встановлювати причинно-наслідкові зв’язки, виявлення скритих залежностей;
• культуру навчальної праці: уміння самостійно знаходити допущені помилки, неточності;
• розвиток творчих здібностей: відчуття протиріччя, становлення до вирішення проблеми, дивергентне мислення.

Тема «Додавання та віднімання дробів з однаковим знаменниками» 5 клас.

Учням пропонується розв’язати дві задачі.

1.     Мама доручила Оленці купити продукти. На хліб дівчинка витратила 3 грн., на молоко−7грн., на овочі та фрукти−8 грн., на морозиво−2 грн. Чи залишились у Оленки гроші після всіх покупок, якщо мама дала їй 20 грн.?
2.     Мама доручила Оленці купити продукти. На хліб Оленка витратила 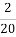всіх грошей, на молоко−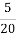, на овочі та фрукти− 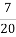і на морозиво− 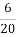усіх грошей. Чи залишились у дівчинки гроші?

Після розв’язку першої задачі, діти розуміють, що дроби треба додати. Виникає проблемна ситуація: як це зробити? Обов’язково знайдуться учні, які запропонують додати чисельники.

При вивченні теми «Додавання дробів з різними знаменниками»(6 клас) пропонується учням розв’язатитаку задачу.

Задача. Мама дала Оленці грошей на сніданок в шкільній їдальні. Повернувшись зі школи, Оленка розповіла, що ½  всіх грошей вона витратила на канапку, 2/5 – на чай, 1/10 – печиво. Мама зрозуміла, що гроші витрачено всі. Як вона дізналась?

Щоб розв’язати цю задачу, потрібно додати дроби ½+2/5+1/10.Учні стикаються із завданням, яке не можна розв’язати, використовуючи наявні в них знання. Виникає думка, що потрібно звести дроби до однакового знаменника.

При вивченні теореми Піфагора (8 клас) доцільно учням запропонувати таку задачу.

Задача.Знайдіть довжину приставленої до будинку драбини, якщо нижній її кінець знаходиться на відстані 3 м від будинку, а верхній – на стику стіни й даху. Висота стіни будинку дорівнює 4 м.

Потім задача формулюється в загальному вигляді. Знайдіть довжину гіпотенузи прямокутного трикутника за його катетами.

Тема «Перша ознака рівності трикутників»(7 клас).

Сьогодні на уроці ми уявимо себе геологами. Нам потрібно встановити палатку. Вона схожа на два трикутника. Для того щоб палатка стояла рівно, треба щоб ці трикутники були рівні. Ми повинні виміряти всі сторони та всі кути? Або є інший шлях?

Вирішення цього питання−мета нашого уроку.

При вивченні теми«Поняття квадратного рівняння. Неповне квадратне рівняння» (8 клас) пропонується учням скласти рівняння до задачі.

Задача. Господарі вирішили огородити ділянку перед фасадом будинку, що прилягає до стіни. Довжина використаної сітки становила 42м, а площа ділянки, яку огородили,− 216м². Яка довжина й ширина ділянки.

                  Учні складають рівняння:

                     х(42-2х)=216,

                      42х-2х²=216.

Проблема−таке рівняння поки що ми розв’язати не можемо, це новий для нас тип рівнянь, що називаються квадратними.

Тема«Аксіоми стереометрії»(10 клас).

Кімнатні двері кріпляться на двох завісах−їх можна вважати «точками». Якщо їх не тримає замок або який-небудь упор, двері можуть вільно обертатися навколо завіс. Це модель якого твердження? (Через дві довільні точки або через одну пряму можна провести безліч площин).

Якщо ж ті чи інші двері замкнути або обперти на який-небудь предмет, вони займуть лише одне певне положення. Обґрунтуйте цей факт з математичної точки зору. (Через три точки, що не лежать на одній прямій, можна провести площину, і до того ж тільки одну).

Дуже часто можна почути, що математика−цариця всіх наук. А чому математикам не присуджують Нобелівську премію? Тому, що А.Б Нобель вважав математику служницею всіх наук. Створюючи мотивацію пізнавальної діяльності, потрібно показувати  дітям служіння математики іншим предметам.

Тема«Розв’язання показниковихрівнянь»(11 клас).

На попередніх уроках ви вже навчилися розв’язувати показникові рівняння і, навпаки, у вас виникли запитання, навіщо вони потрібні. Можна навести багато задач в різних галузях. Візьму одну таку задачу, яка має відношення до всіх українців. 26 квітня 1986 рік − день аварії на Чорнобильській атомній електростанції, внаслідок якої територія України була забруднена радіоактивною речовиною. З фізики відомо, відношення початкової до кінцевої N кількості радіоактивної речовини обчислюється за формулою N₀/N=2^x/T, де х− час після аварії, Т− період напіврозпаду радіоактивної речовини.

Одним з найнебезпечніших є атоми радону. Для нього Т≈4 доби.

Задача. Через який час після аварії кількість радіоактивних атомів радону зменшиться у 1024 рази, тобто 2^х/T=1024? (Відповідь: через 40 діб).

Тема«Визначений інтеграл»(11 клас).

Інтеграл−це ключ, який відчиняє ворота між фізикою і математикою. Тут вони поєднуються в єдине ціле. Фізика вивчає різні явища й процеси, які пов’язані зі змінними величинами, обчислювати які значно легше за допомогою визначеного інтеграла.

Давайте згадаємо ті задачі, що приводять до поняття визначеного інтеграла.

Величини	Співвідношення	Знаходження похідної	Знаходження інтеграла
S−переміщення; v−швидкість	∆S=v(t)∆t	v(t)=S(t)
A−робота;F−сила	∆A=F(t)∆t	F(t)=A′(t)
q−електричний струм; І−сила струму	∆q=I(t)∆t	I(t)=′(t)
Q−кількість теплоти;с−теплоємкість	∆Q=c(t)∆t	c(t)=Q/(t)
m−маса; −густина	∆m=(x)∆(x)

Заповніть порожній стовпець таблиці – мета нашого уроку

Узагальнюючи вивчення теми «Подібність трикутників»(8 клас) можна поставити запитання: «Як виміряти висоту або довжину об’єкта, що є недоступним?»

Учні стикаються із завданням знаходження ширини річки, не перепливаючи її, або визначення висоти дерева не піднімаючись на його вершину. Неприступну відстань замінюють проміром іншої відстані, що легко піддається безпосередньому виміру. Для цього використовують відомі співвідношення у геометрії – ознаки рівності трикутників, а  також ознаки подібності трикутників.

Проблемну ситуацію на уроці можна створити за допомогою завдань із практичним змістом, особливо при вивченні теми «Математичне моделювання»(9 клас). Розв’язування прикладних задач із різними сюжетами дає можливість пов’язати вивчення теорії з практикою.

Прикладом цього типу задач можуть бути такі:

Задача.Один кінець драбини, довжина якої 13 м, знаходиться на відстані 5 м від основи будівлі, на яку спирається драбина. Знайти висоту будівлі.

Розв’язування цієї задачі зводиться до знаходження невідомого катета прямокутного трикутника, тобто до вивчення наслідків з теореми Піфагора.

Уведення поняття лінійного рівняння з двома зміннимиу 7 класі можна здійснити за допомогою такої задачі:

Задача. Потрібно прокласти водопровід довжиною 150 м, маючи труби довжиною 5 м і 7 м. Скільки труб кожного виду потрібно взяти?

Розв’язування.Нехайх – кількістьтруб першого виду, у – кількість труб другого виду, то маємо рівняння 5х+7у=150. Але з таким рівнянням учні стикаються вперше, тому виникла суперечність між тим, що учні знали до цього і необхідністю розв’язати практичну задачу. Отже нові знання необхідні.

«Мистецтво стає більш науковим, а наука – художньою, розлучившись біля підніжжя, вони зустрінуться коли-небудь  на вершині», – сказавГ.Флобер. З різних причин математика проникла в літературу, мабуть тому що осягнення драматичного змісту життя потребувала його логічного впорядкування. Мотивація пізнавальної діяльності шляхом використання художньої, науково-популярної літератури, живопису– один з етапів розв’язування навчальних проблем. Це дозволяє виховувати в учнів:

•    патріотизм, гуманізм, соціальну активність;
•    свідоме відношення до праці;
•    культуру розумової праці;
•    прагнення, готовність та уміння вносити елементи прекрасного в своє життя;
•    уміння проявляти себе в мистецтві;
•    багату уяву, відчуття краси тощо.

У 5 класі вивчаються теми «Знаходження дробу від числа», «Знаходження числа за його дробом». Учні із задоволенням розв’язують наступні задачі.

Задача.Іван Франко прожив у Львові 40 років, що становить ⅔ його життя.Скільки років прожив письменник? (60 років)

Задача. Великий Каменяр 1/10 частину свого життя провів у рідному селі Нагуєвичи. Скільки років прожив Іван Якович у батьківському домі? (6 років)

Задача.У селі Криворівня Івано-Франківської області працював і відпочивав Франко 1/5 свого життя. Скільки років жив Франко у Криворівні? (12 років)

Задача. Яка відстань від рідного села Франка до Дрогобича, якщо ¼ шляху становить 4 км? (16 км)

Під час вивчення формул скороченого множення учням пропонується репродукція картини М. Богданова – Бельського «Усний рахунок. У народній школі С.О. Рачинського». Хитрі математичні задачки можна виявити в картинній галереї. Вчитель запропонував молодшим школярам усно розв’язати зображену на дошці задачку.

К. Вейєрштрасс сказав: «Не можна бути справжнім математиком, не будучи трохи й поетом». Художня та науково−популярна література, цікаві факти з життя літераторів, ситуацій, у які вони потрапляли допомагають зробити мотивацію навчання цікавою, захоплюючою.

Геометрія, 11клас. Тема «Конус. Об’єм конуса».

Пушкін О.С. «Скупий лицар» сцена 2.

…Читал я где−то,

Что однажды воинам своим

Велел снести земли по горсти  в кучу,

И гордый холм возвысился, и царь

Мог с вышины с весельем озирать

И дол, покрытый белыми шатрами,

И море, где бежали корабли.

Геометрія, 9 клас. Тема «Перетворення подібності на площині».

1.                   Сайрес Сміт із твору Ж. Верна своїми знаннями з геометрії зумів визначити координати острова, де вони опинилися, і тим самим врятував життя своїм друзям.

Сайрес Сміт взяв із собою пряму рівну жердину довжиною біля дванадцяти футів− довжину він визначив за власним зростом, який він знав абсолютно точно. ГербертуСайрес Сміт доручив нести висок, тобто гнучку ліану, до кінця якої був привішений звичайний камінь.

Зупинившись приблизно кроках у двадцяти від узбережжя і кроках у п’ятистах від гранітного кряжу, Сайрес Сміт устромив жердину в пісок і старанно випрямив її, добившись шляхом вивірки виском, щоб вона стояла перпендикулярно до площини обрію.

Зробивши це, Сайрес Сміт відійшов і ліг на землю на такій відстані, щоб у полі його  зору знаходився і верхній кінець жердини, і гребінь гранітної стіни. Це  місце він позначив на піску кілочком і, коли повернувся до Герберта, спитав:

• Ти знайомий з геометрією?
• Трохи, містере Сайрес,− відповів Герберт, остерігаючись ускочити в халепу.
• Пам’ятаєш властивості подібних трикутників?
• Так,− відповів юнак,− у подібних трикутників відповідні сторонипропорційні одна одній.
• Так от, дитя моє, у мене тут два подібних прямокутних трикутники, один менший, у ньому двома сторонами будуть жердина, встромлена перпендикулярно в пісок, і пряма, що дорівнює відстані від нижнього кінця жердини до кілка, а гіпотенузою− мій промінь зору; у другого трикутника сторонами будуть стрімка лінія гранітної стіни, висоту якої нам треба виміряти, відстань від кілка до підніжжя стіни, а в якості гіпотенузи – мій промінь зору, тобто продовження гіпотенузи першого трикутника.
• Зрозумів, містере Сайрес! Я все зрозумів!− викликнув Герберт.

Відстань від кілка до жердини пропорційна відстані від кілка до підніжжя стіни, а висота жердини пропорційна висоті стіни.

• Правильно, Герберте,− підтвердив інженер.− І коли ми виміряємо обидві відстані від кілка, то, знаючи висоту жердини, ми швидко розв’яжемо пропорцію і таким способом визначимо висоту стіни, що позбавить нас від мороки вимірювати її безпосередньо. (Ж. Верн «Таємничий острів»)

А чи зможемо й ми скористатися знаннями з геометрії?

2.                   Знання з геометрії можуть рятувати життя. Пропоную вашій увазіуривок з твору А. Демидова «Розвідка ріки». Відділенню старшого сержанта Куприянова було наказано виміряти ширину річки, через яку необхідно було організувати переправу.

Коли відділення Куприянова підібралось до кущів біля річки івоїни залягли, сам Куприянов разом з солдатом Карповим підібралися ближче до річки, звідки добре було видно зайнятий фашистами берег. У таких умовах вимірювати ширину річки необхідно було на око.

• Ну як, Карпов, скільки?− спитав Куприянов.
• Як на мене, то не більше ніж 100−110 м,− відповів Карпов.

Куприянов був згодний зі своїм розвідником. Але для контролю вирішив виміряти ширину річки за допомогою «козирка»…

Вивчити різні способи вимірювання недосяжних відстаней− мета нашого уроку.

Засобами стимулювання учнів до математичної діяльності, створенню пізнавального мотиву, активізації мислення є дидактичні ігри, ігрові прийоми та ігрові ситуації, що допомагають у формуванні в учнів мотиваційної сфери. Длястворення ігрових ситуацій використовують цікаві задачі, загадки, оповідання, частини літературних творів та інше.

При вивченні геометричного матеріалув 5 класі пропонуються загадки.

1.Буває і великий, і малий, і повний

          Ним карають у дитинстві.

          Іноді він буває прямий,досить часто тупий, але переважно гострий.

          Що це?( Кут)

          2.Кругла куля не проста,

          Голуба, велика:

          Без будинків там міста,

          Без води там ріки,

          Без людей і без землі, і шляхи і гори,

          Всі земні простори.

          Що це таке? (Глобус)

Створити ігрову ситуацію на уроці дозволяє гра «Чи знаєте ви, що?…».

Тема«Довжина кола й дуги»

Чи знаєте ви,що?…

Колову форму тіл люди спостерігали з давнини, наприклад обрис повного Місяця. Близько 6 тис. років у Вавилоні було знайдено колесо. Цей винахід відіграв важливу роль у житті людини для полегшення важкої праці. Колеса почали виготовляти різних розмірів. Постало питання про витрати матеріалу, а разом з тим і проблема знаходження довжини кола і площі круга.

Далі виконується відома кожному вчителю практична робота по знаходженню відношення довжини кола до діаметра. Учні мають  приблизно однаковий результат 3,14 . Після цього вводиться поняття числа π, та вчительрозповідає про цечисло.

 

 

 

У такий спосіб учні отримують додаткову інформацію, що сприяє їх інтелектуальному розвитку.

Тема «Додавання й віднімання натуральних чисел» (5 клас).

Жили були добрі й злі гноми. Добрі гноми жили на землі. Вонивирощували дивовижні квіти, очищали водойми, ліс, допомагали людям зберігати врожай у роки зі спекотним літом. Але люди, ясна річ, навіть не підозрювали про їхнє існування. Тим часом злі гноми жили під землею й намагались людям нашкодити. Добрі й злі гноми завжди ворогували між собою.

Упродовж багатьох років добрі гноми намагалися створити в своїх лабораторіях формулу очистки повітря на Землі. Адже ви розумієте, наскільки це потрібно, особливо зараз. Дізнавшись про це, злі гноми викрали таку важливу, уже майже готову формулу, щоб знищити людей, а заразом і їхніх помічників− добрих гномів.

До вас, учні 5 класу, надійшло зашифроване послання. Розшифрувати його зможуть тільки такі же шифрувальники, як ви. Дорослим із цим завданням ніколи не впоратися.

А тепер до роботи.

Формуванню пізнавальних інтересів і позитивних мотивів навчальної діяльності допомагає застосування елементів історизму, що сприяє формуванню в школярів навичок пошукової діяльності, вмінь посильно проявляти себе у мистецтві, креативності та критичного мислення. Це дає змогу подати учням «біографію» нового терміну, історію розвитку відповідного поняття.

Тема «Лінійне рівняння з однією змінною» (7 клас).

Ми починаємо вивчати алгебру з розділу «Рівняння». І це недаремно, тому що алгебра почалася і довго розвивалася саме як наука про рівняння. Навіть сама назва «алгебра» утворилася від слова «аль−джебр», яке відомий узбецький математик ІХ ст. МуххамедАль− Хорезмі використовував у своїй книзі про розв’язування рівнянь.

Перші рівняння люди вміли розв’язуватидуже давно. Єгипетські вчені майже 4 тис. років тому невідоме число в рівнянні називали «хау» (у перекладі −«купа») і позначали спеціальним знаком. У папірусі, що дійшов до нас, є така задача:

Купа і її сьома частина становлять 19. Знайдіть купу.

Сьогодні ця задача виглядала б так: «Сума невідомого числа і його сьомої частини дорівнює 19. Знайдіть невідоме  число».

Тема «Теорема Піфагора» (8 клас).

   Індійський математик Бхаскари, ХІІ ст.

На берегу реки рос тополь одинокий.

                 Вдруг ветра порыв его ствол надломил.

                 Бедный тополь упал. И угол прямой

                 С течением реки его ствол составлял.

                 Запомни теперь, что в том месте река

                 В 4 лишь фута была широка.

                 Верхушка склонилась у края реки.

                 Осталось 3 фута всего от ствола,

                 Прошу тебя, скоро теперь мне скажи:

                 У тополя как великависота?

Тема «Арифметична та геометрична прогресії» (9 клас).

1.Послідовність –явище, без перебільшення, унікальне. Історія виникнення послідовностей сягає глибини віків. Вже в клинописних табличках вавилонян, у єгипетських папірусах, датованих ІІ тисячоліттям до н. е., зустрічаються задачі на арифметичну і геометричну прогресії.

2.Задача. (З Єгипетського папірусу близько 2000 р. до н. е.). У семи осіб по сім кішок, кожна кішка з’їдає по сім мишей, кожна миша з’їдає по сім колосків ячменю, з кожного колоска ячменю може вирости по сім мір  зерна. Скільки мір зерна збережеться завдяки цим кішкам?

3.Задача.(Задача Ейлера). Один чоловік продає свого коня за кількістю підкованих цвяхів, яких у нього 32. За перший цвях він просить 1 коп., за другий−2 коп., за третій−4 коп., за четвертий−8 коп. тощо. Скільки всього він просить за коня?

Важливу роль у створенні мотивації пізнавальної діяльності учнів на уроці грають інтерактивні технології. Мотиваційні інтерактивні методи навчання – це способи взаємодії учасників навчального процесу. Кожен учасник визначає власну позицію у ставленні до способів діяльності класу, окремих учнів, учителя, самого себе.

Серед таких методів можна назвати «Асоціювання», «Кубування», «Реклама».

«Асоціювання»– ця навчальна стратегія дозволяє брати участь у процесі мислення всім учням, міркувати вільно та відкрито. Для проведення асоціювання рекомендовано такий алгоритм:

1.        На дошці записано ключове слово теми, наприклад десяткові дроби.
2.        Навколо цього слова записують усі відомі учням факти, наприклад кома, знаменник дробу 10, 100 і т. д., порівняння дробів, округлення дробів, ціла частина, дробова частина, додавання, множення, ділення, віднімання дробів.
3.        Між записаними фактами встановлюють зв’язки за допомогою стрілок, наприклад: кома→ціла частина; кома → додавання дробів; кома → множення дробів і т. д.

«Кубування». Цей метод використовують коли деяке поняття розглядають різнобічно. На гранях куба записані запитання до теми «Паралельні прямі» (7 клас).

1.        Опиши: прямі, що не перетинаються.
2.        З чим пов’язані: точки, прямі, площина.
3.        Проаналізуй: складаються з двох прямих, що не мають спільних точок.
4.        Застосуй: зошити в клітинку,  віконні рами.
5.        Оціни: «за» – проектуванняархітектурних споруд, меблів.

«Реклама». Цей метод зацікавлює учнів своєю новизною, сучасністю. Адже вони бачать, яке велике значення в житті має реклама. Учням треба задати домашнє завдання підготувати рекламу на якесь математичне поняття, застосування теми та ін. На уроці «йде трансляція реклами».

Варіанти реклам, розроблені учнями при вивченні теми «Лінійне рівняння».

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Отже, найважливіше завдання школи – сприяти засвоєнню учнями глибоких і міцних знань з математики, формуванню вмінь і навичок застосовувати їх у житті та на практиці. Щоб навчити дітей думати, відкривати, винаходити, вчитель повинен багато вигадувати, знаходити і відкривати.