Переміщення (рух) та його властивості

Урок геометрії в 9 класі

Мета: Навчальна складова Узагальнити та систематизувати знання учнів з теми: «Геометричні перетворення на площині». Удосконалити вміння розв’язувати задачі з цієї теми. Показати важливість математики у повсякденному житті. Розвиваюча складова Розвивати пізнавальний інтерес. Розвивати пам’ять, увагу, образно-геометричне мислення. Розвивати інтелектуальні та творчі здібності учнів. Розвивати вміння виділяти головне, робити висновки. Виховна складова Виховувати культуру математичного мовлення. Виховувати почуття відповідальності, взаємодопомоги.

А В С

Перетворення однієї фігури в іншу, при якому зберігається відстань між точками, називається рухом.

.А .А

Точки, що лежать на прямій, при русі переходять в точки, що лежать на прямій, і зберігається порядок їх взаємне розміщення. А В С А В С Отже: при русі прямі переходять в прямі, півпрямі – в півпрямі, відрізки – в відрізки, зберігаються кути між півпрямими.

Робота з підручником №17.3 Усно:

Робота з підручником №17.6 №17.10(усно)

Центральна симетрія Поворот Осьова симетрія Паралельне перенесення

О А В О Точка А симетрична точці В відносно центра симетрії – точки О

Центральна симетрія Точка Х симетрична точці X’ відносно точки О О – центр симетрії, ОХ = ОX’

Симетрія відносно точки А1 А О

Симетрія відносно точки А1 А О побудувати точку А1, симетричну точці А відсно точки О

Симетрія відносно точки Побудувати відрізок А1В1, симетричний відрізку АВ відсно точки О А В А1 О В1

а А В Точка А симетрична точці В відносно прямої а – осі симетрії n

Осьова симетрія Точка Х симетрична точці X’ відсно прямої а а – вісь симетрії a

Симетрія відносно прямої А a a a a А1 в

Симетрія відносно прямої А a А1 Побудувати точку А1, симметричну точці А відсно прямої а

Симетрія відносно прямої В а А А1 В1 Построить отрезок А1В1, симметричный отрезку АВ относительно прямой а

Домашнє завдання Опрацювати с.157-162 №17.7

О А В О – центр поворота кут АОВ – кут поворота напрям поворота – за годинною стрілкою О Х Напрям поворота – за годинною стрілкою

Поворот Точка Х переходе в точку Х’ Ŀ а – угол поворота

Перетворення фігури F, при якому її довільна точка (х; у) переходить в точку (х+а; у+в) називається паралельним перенесенням. Паралельне перенесення задається формулами В які точки при цьому паралельному перенесенні переходять точки О(0;0), А(0;4), В(-4;1)?

В О Р А Направлений відрізок ОР задає паралельне перенесення Промені АВ и ОР одинаково направлені АВ = ОР Паралельне перенесення визначається як перетворення, при якому точки зміщуються в одному і тому ж напрямі на одну і ту ж відстань.

Преобразование, при котором сохраняется расстояние между любыми точками XY = X’Y’ Х Х’ Y Y’

Паралельне перенесення Точка Х (х,у) переходе в точку Х’ (x + a, y + b), де a і b – однакові для всіх точок

А В С А1 В1 С1

Перетворення фігури F у фігуру F‘ називається перетворенням подібності, якщо при цьому перетворенні відстань між точками змінюється в одне й теж число разів.

Перетворення фігури F у фігуру F‘ називається перетворенням подібності, якщо при цьому перетворенні відстань між точками змінюється в одне й теж число разів. X X’ Y Y’ X’Y’ = kXY, где k – коєфіцієнт подібності

О – центр гомотетії OX’ = kOX О Х Х’ Гомотетією з центром О і коефіцієнтом k≠0 називається геометричне перетворення, яке довільно взяту точку А переводить в таку точку А‘, що ОА‘=k∙ОА

Композиція рухів

За якою ознакою складені наступні літери алфавіту:

вертикальна вісь симетрії горизонтальна вісь симетрії вертикальна та горизонтальна вісь симетрії літери не мають ні горизонтальної ні вертикальної вісі симетрії

- це абсолютний прояв симетрії в літературі.  — це слова або вислови, які читаються однаково як зліва направо, так і справа наліво.

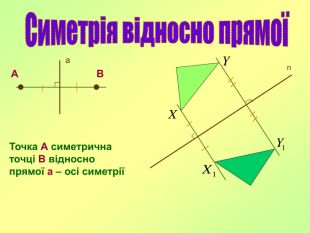
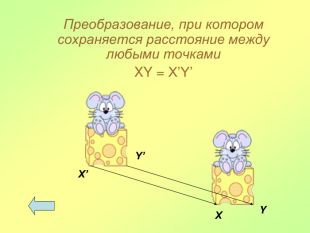
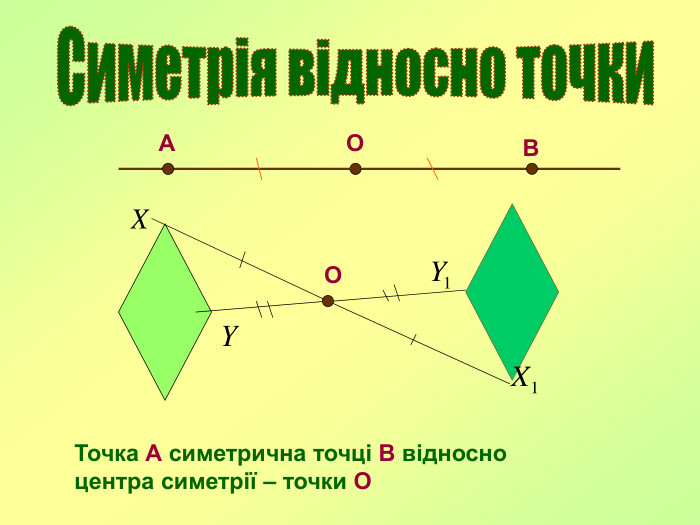
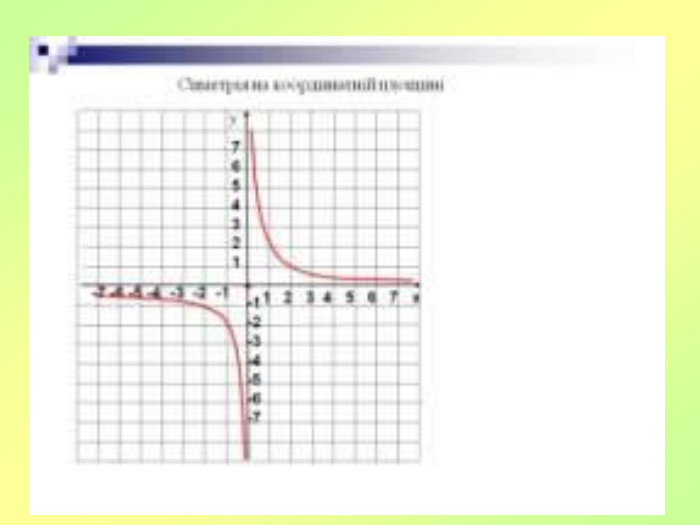
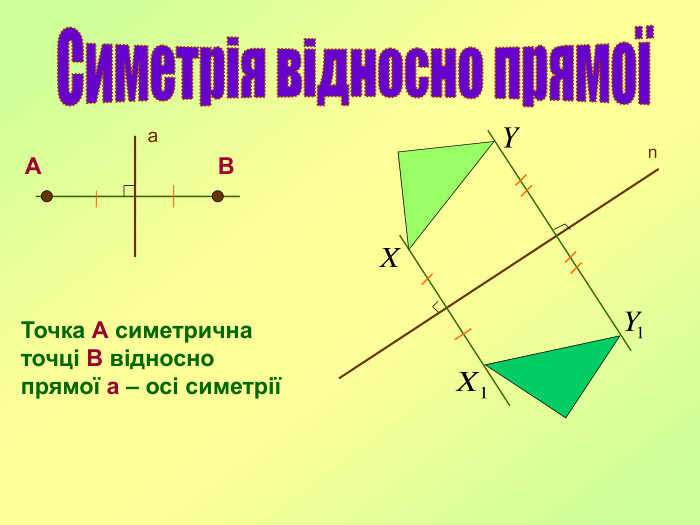
Поняття симетрії: В давні часи слово “симетрія” використовувалося як “гармонія”, “краса”. Дійсно, в перекладі з грецької, симетрія – це “пропорціональність, однаковість в розположенні частин”. Симетрія — властивість об'єкту відтворювати себе при певних трансформаціях, які називаються операціями симетрії.

Симетрія також використовується в дизайні

Симетрія поширена і в геральдиці

Кожна сніжинка – це маленький кристал замерзлої води. Форма сніжинок може бути найрізноманітнішою, але всі вони підпорядковані симетрії.

Симетрія не залишилась лише геометричним поняттям, а й віднайшла себе у найрізноманітніших сферах нашого життя.