Перетворення цілих виразів

Тема. Перетворення цілих виразів

Мета: узагальнити та систематизувати знання, вміння, навички учнів; підготуватися до тематичної контрольної роботи.

Тип уроку: узагальнення та систематизація знань.

Хід уроку

I. Організаційний момент

Учитель перевіряє готовність учнів до уроку та повідомляє тему.

II. Перевірка домашнього завдання

1. Вправи № 1 та 2 із домашнього завдання є вправами на закріплення на­вичок, формування яких почалося на попередньому уроці. Тому перевірку цієї частини домашнього завдання виконуємо або вибірково (у «слабких» учнів) або спонукаємо учнів до самоперевірки та відповідаємо на запитання, що виникли в учнів під час розв'язування цих завдань.
2. Робота з випереджальним домашнім завданням,

 Ця частина домашнього завдання є дуже важливою, бо є фундамен­том для здійснення узагальнення та систематизації та, можливо, й  корекції знань,  умінь та навичок напередодні тематичної контрольної роботи.  Тому цю  частину домашнього завдання перевіряємо ретельно. Учні презентують виписані поняття та аргу­ментують свій вибір.

Наступним кроком повинно йти встановлення зв'язків (логіки) між виписаними елементами й поняттями. Після обговорення можемо зроби­ти певні висновки.

Під час роботи з цілими виразами (а саме такі розглядаються в 7 класі) ми здійснюємо два обернені види перетворень: а) записати вираз у вигляді многочлена (суми); б) перетворити многочлен (суму) у добуток (розкласти на множники).

Можна виділити такі способи тотожних перетворень цілого виразу у многочлен:

1. розкриття дужок;
2. зведення подібних членів многочлена;
3. перетворення одночленів у одночлени стандартного вигляду;
4. додавання і віднімання многочленів;
5. множення одночлена на многочлен та многочлена на многочлен;
6. застосування формул скороченого множення.

Нагадуємо такі способи перетворення суми в добуток (розкладання на множники):

1. винесення спільного множника за дужки;
2. застосування формул скороченого множення;
3. групування та деякі спеціальні прийоми (перегрупування, зведення до різниці квадратів).

Основні види задач, під час розв'язування яких використовують названі перетворення:

1. обчислення значень виразів;
2. розв'язування рівнянь;
3. доведення подільності;
4. пошук найбільшого або найменшого значення виразу.

Після обговорення складаємо схему:

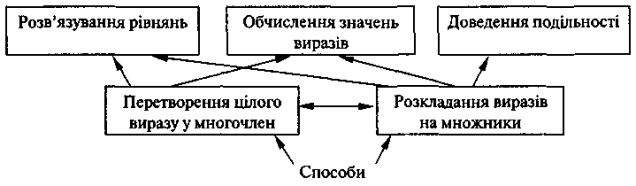
1) a + (b – c) = a + b – c  

2) а – (b – с) = а – b + с

3) а(b + с) = аb + ас

4) (а ± b)² = а² ± 2аb + b²

5) (а – b)(а + b) = а² – b²

6) (а ± b)(а² аb + b²) = а³ ± b³

III. Формулювання мети й завдання уроку

 Після виконаної роботи з узагальнення матеріалу формулюємо мету уроку: 1) узагальнити навчальний матеріал щодо способів перетво­рень деяких виразів; 2) узагальнити та систематизувати вміння ви­конувати названі перетворення та навички застосування під час розв'язування задач.

IV. Узагальнення та систематизація вмінь та навичок

 Цей етап уроку передбачає узагальнення засвоєних умінь та нави­чок учнів на конкретних типових завданнях, а також, у разі необхідності, корекції знань та вмінь учнів. Тому цей етап уроку ба­жано провести у вигляді роботи у групах, причому групи формуються з учнів, що мають схожі проблеми, тобто будуть опрацьовувати й ко­ригувати одні й п самі вміння і навички Для того щоб сформувати групи, учням пропонується для самостійного виконання тестове завдання.

1. Розкладіть на множники 3а² – 3:

1) 3(а² – 3); 2) 3(а² – 1); 3) 3(а – 1)²; 4) 3(а – 1)(а + 1).

2. Виділіть повний квадрат із виразу х² – 14х + 50:

1) х² + (-14x + 50); 2) (x – 7)²; 3) (х – 7)² + 1;   1)г > 1; 4) (х – 7)² +50.

3. Розв'яжіть рівняння х³ – 6х² – 19х = 0:

1) х = 0; 6x² = 0; 9х = 0;   2) х(х² – 6х + 9) = 0; х = 0 або х² – 6х + 9 = 0;

3) х(х – 3)² = 0; х = 0 або х – 3 = 0;   4) х³ – 6х² = -9х.

4. Доведіть, що вираз (п + 1)² – (п – 1)² (ділиться на 4):
   l) (п + 1)² – (п – 1)² = (п + 1 – (п – 1))(п + l + п – l) = 2 ∙ (2п) = 4п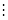 4;

2) (п + 1)² – (п – 1)² = п² + 1 – п² – 1 = 0 ділиться на 4;

3) (п + 1)² – (п – 1)² = п² + 2п + 1 – (п² – 2п + 1) =

     = п² + 2п + 1 – п² + 2п – 1 = 4п 4;

4) інший варіант.

Після проведення і перевірки тестів учні об'єднуються в гомогенні групи, і наступна робота проводиться в групах із подальшою презентацією результатів роботи.

Група № 1. Тема. Застосування різних способів розкладання многочле­нів на множники.

Завдання 1. Повторіть за підручником або зошитом теорію: алгоритм за­стосування різних способів розкладання многочленів на множники.

Завдання 2. Використовуючи повторений алгоритм, розкладіть на множники:

1) х³ – 4х; 2) х⁴у² – х²у⁴;  3) 1,44а² – b²;           4) (с² + 1)² – 4с²;

5) а² – 2аb + b² – 1;        6) 25т² – (4т – 4)²;  7) х² – у² – х – у;

8) 2a² – 2b² – (a – b)²;     9) a³ – 64;                 10) а⁵ – а³ + а² – 1.

Група № 2. Тема, Виділення повного квадрата двочлена.

Завдання 1. а) За підручником або конспектом у зошиті повторіть фор­мули квадрата двочлена й алгоритм виділення квадрата двочлена з квадрат­ного тричлена; б) як визначити найменше значення виразу х² + а?

Завдання 2. а) Подайте у вигляді квадрата двочлена х² + 8х + 16;

б) виділить квадрат двочлена з виразу х² + 8х + 18;

в) яких значень набуває вираз, здобутий у п. б)? Яке значення є наймен­шим? При якому значенні змінної вираз набуває цього значення?

Група № 3. Тема. Розв'язування рівнянь із застосуванням різних спо­собів, покрокового перетворення виразів.

Завдання 1. За конспектом, довідником або підручником повторіть: 1) як звести розв'язування рівняння до розв'язування лінійного рівняння з однією змінною; 2) як розв'язати рівняння, якщо ліва частина його є до­бутком двох або більше лінійних множників, а права частина є нулем; 3) яку властивість використати, щоб розв'язати рівняння, якщо ліва час­тина є сумою двох невід'ємних доданків, а права — нулем.

Завдання 2. Розв'яжіть рівняння і прокоментуйте хід розв'язання.

1) x² – 9х = 0;    2) у(у² + 3) = 4у;

3) х³ – 5х² – х + 5 = 0; 4*) (х² – 1)² + (х² – х)² = 0.

Група № 4. Тема. Доведення подільності.

Завдання 1.1) Яке число називають дільником даного числа?

2) Як довести, що вираз А ділиться на дане число?

Завдання 2. Доведіть, що:

1) при кожному цілому значенні п значення виразу

(2п + 7)(8п – 8) – (4п + 5)² не ділиться на 6;

2) значення виразу ділиться на дане число:

а) 401² – 199² на 600; б) 58³ + 42³ на 100; в) 8²⁵ – 64¹² на 7;

г) 16⁹ – 32⁸ + 8¹² на 7;

д*) різниця квадратів двох цілих чисел, які не діляться на 3, кратна 3.

V. Підсумки уроку

 Знову повертаємось до схеми, складеної на початку уроку, й повто­рюємо основні теоретичні моменти й способи дій.

VI. Домашнє завдання

Домашня контрольна робота

№ 1. Спростіть вираз:

1) (а – 6)(а + 6) + (3 – а)² – (2а + 1)² – (а – 3)(а + 4);

2) (а² – b²)(а² + b²)(а⁴ + b⁴) + а⁸ + b⁸.

№ 2. Розкладіть на множники:

1) 9у² – 16; 2) 3х² – 3у²; 3) 27а³ – b³; 4) b⁶ – 4b⁴; 5) 0,8а³ + 0,4а² + 0,4а⁴;

6) т³ – п³ + 3т² + 3тп + 3п²; 7) а² + b² + с² – х² + 2аb + 2bс + 2са.

№ 3. Розв'яжіть рівняння:

1) (х² – l)(х² + l)(x⁴ + 1) = x⁸ + 4x; 2) х² – 9 = х – 9х².

№ 4. Доведіть, що:

1) вираз -х² + 10х – 27 набуває лише від'ємних значень;

2) якщо число п від ділення на 5 дає остачу 3, а число т — остачу 4; число п² + т² ділиться на 5.