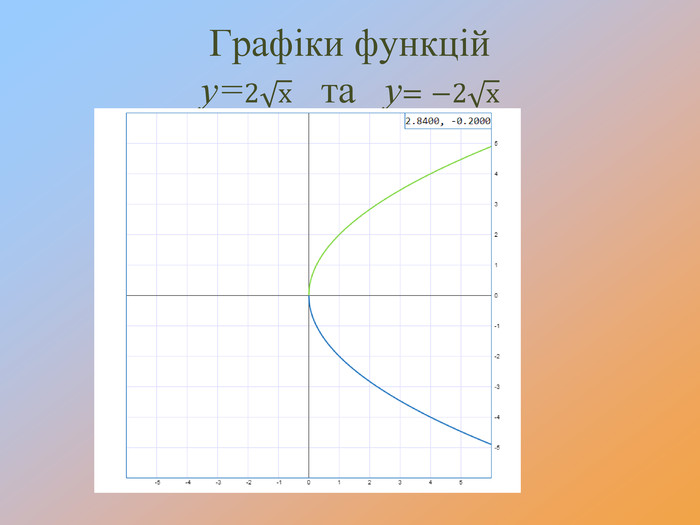
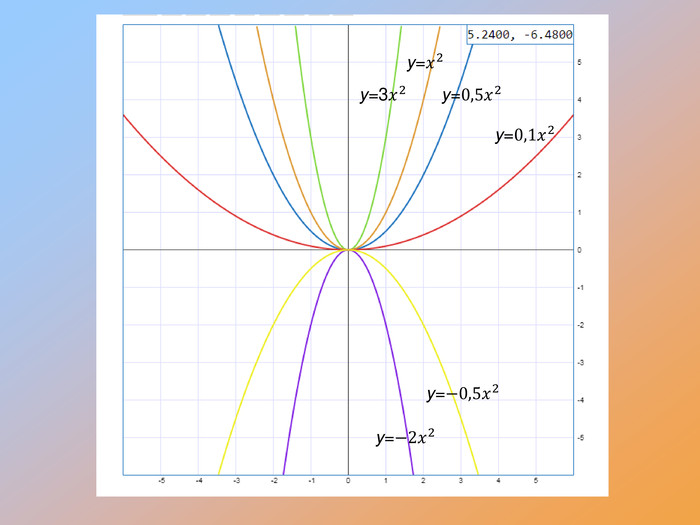
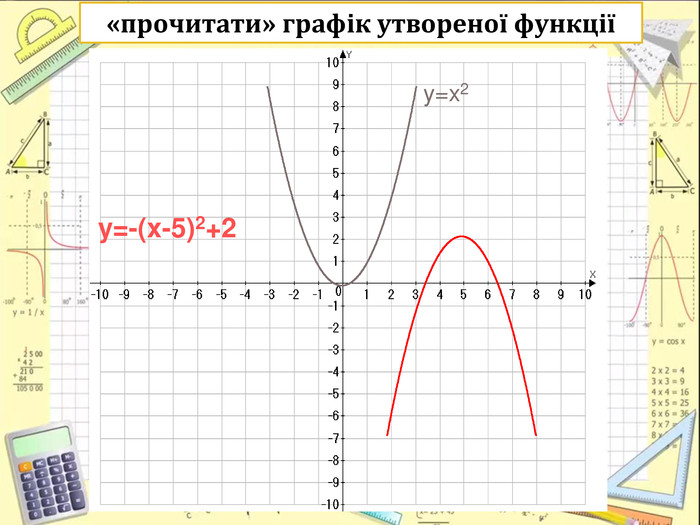
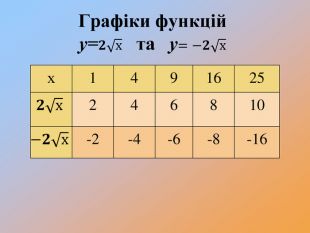
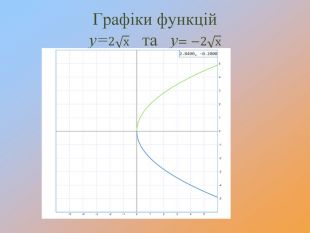
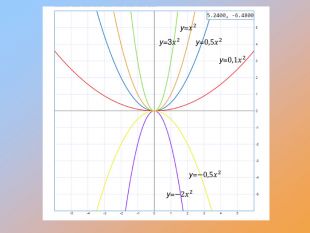
Перетворення графіків функцій
АЛГЕБРА. 9 КЛАС
Тема. Найпростіші перетворення графіків функцій
Мета:
навчальна: формувати поняття найпростіших перетворень графіків функцій через виконання конкретних завдань, вчити формулювати правила перетворення графіків функції, формувати знання учнів про основні види геометричних перетворень графіків функцій та про рівняння функції, що задається цим перетворенням, формувати вміння і навички «читати» графіки функцій (тобто за готовими графіками задавати рівняння функцій), виконувати нескладні перетворення графіків функцій.
розвивальна: розвивати просторову уяву та спостережливість; формувати вміння порівнювати, аналізувати, узагальнювати, робити висновки; формувати навички роботи в різних онлайнових навчальних середовищах
виховна: виховувати інформаційну культуру, впевненість в собі, самостійність і зосередженість.
Тип уроку: засвоєння нових знань, урок-практикум
Обладнання: шаблон інтелектуальної карти знань (додаток 1), мультимедійний проектор, презентація (програма Power Point), персональні комп’ютери підключені до мережі Інтернет, програми для побудови графіків функцій
(урок проходить у комп’ютерному класі)
Епіграф: Скажи мені, і я забуду.
Покажи мені, і я запам’ятаю.
Дай мені діяти самому,
І я навчусь.
Конфуцій
ХІД УРОКУ
І. ОГРАНІЗАЦІЙНИЙ ЕТАП
Привітання, перевірка готовності учнів до уроку, пригадування правил поведінки та техніки безпеки у комп’ютерному класі.
4-грудня-День інформатики,
тому ми будемо працювати з онлайновим середовищем
під час перевірки д/з та вивчення нової теми
-Ви чудово знаєте правила роботи за комп’ютером та іншими пристроями , дотримуйтесь їх.
-За допомогою телефона увійдіть на платформу Kahoot!
ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ
Поки завантажується Kahoot!:
- Яка тема вивчається?(«Функція»- основна тема курсу «Алгебра»,тому на ЗНО 10% завдань з даної теми)
-Пригадаємо основні поняття даної теми(залежна і незалежна змінна, область визначення та область значень функції, проміжки зростання та спадання , проміжки знакосталості, парність функції,…..)- ХМАРКА СЛІВ
- Чим являються більшість з названих термінів для функції? (властивостями)
Вправа1: «Властивості функцій»- kahoot!
(за допомогою вправи учні повторюють властивості функцій).
Оцінки після перегляду ваших відповідей!!!

ІІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
-Перевіримо як ви пам’ятаєте основні функції та їх графіки.
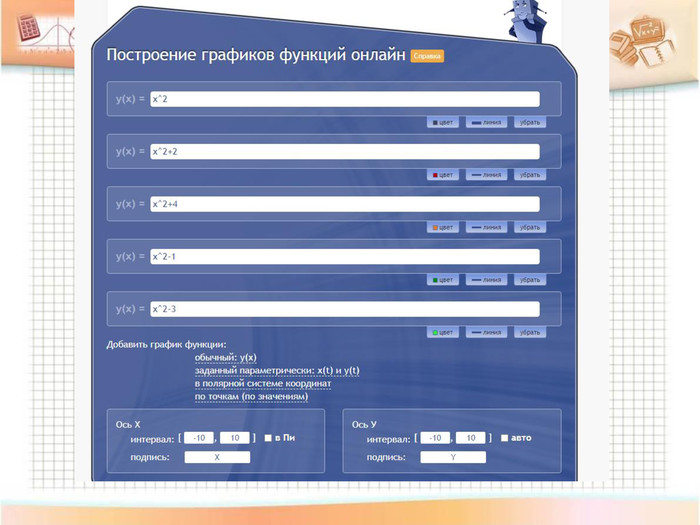
-Працюємо разом зі мною з онлайн-сервісом LearningApps
Вправа2: «Графіки елементарних функцій»
-я демонструю на інтерактивній дошці,
-ви-учні, результат пишете на пластикових дощечках,
-а один учень- відповідність демонструє на дошці,
аби ви весь урок мали змогу звертатись до основних функцій
Виконання вправи (за допомогою вправи учні пригадають графіки основних функцій)
ІV. МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ. ОГОЛОШЕННЯ ТЕМИ, МЕТИ ТА ЗАВДАНЬ УРОКУ
Тема уроку:
«ПЕРЕТВОРЕННЯ ГРАФІКІВ ФУНКЦІЙ»
-На минулих уроках ми навчилися визначати властивості функції коли функція задана рівнянням або графіком.
-Як ви вже зрозуміли, коли побудований графік функції, нам легше та простіше визначити властивості даної функції.

V. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
Скажи мені, і я забуду.
Покажи мені, і я запам’ятаю.
Дай мені діяти самому,
І я навчусь.
Конфуцій
-Учні класу самостійно досліджували окремі види перетворень графіків функцій і зараз продемонструють результати (Технологія перевернутий клас)
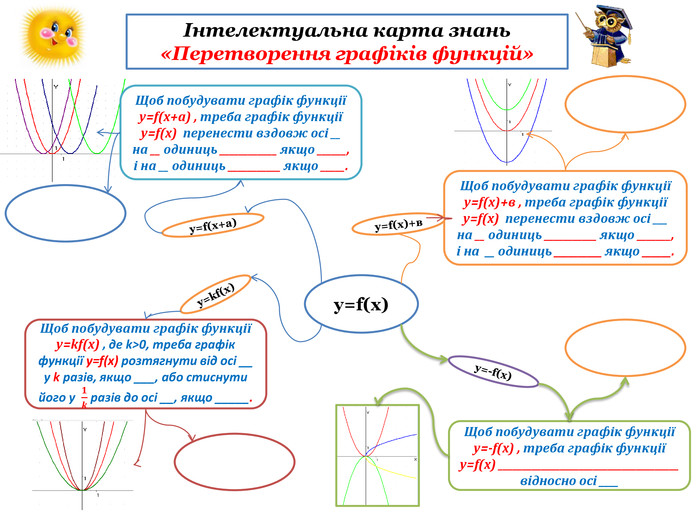
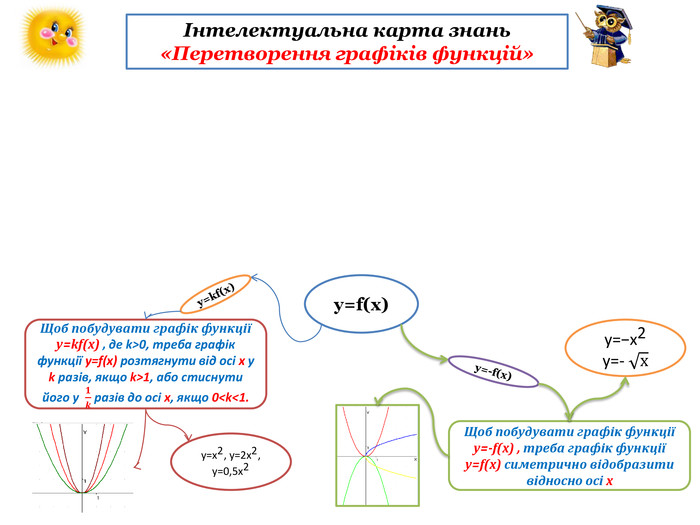
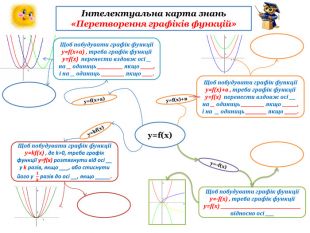
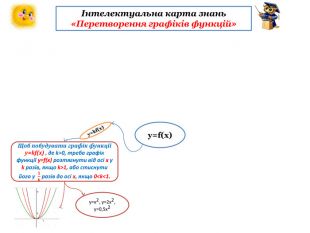
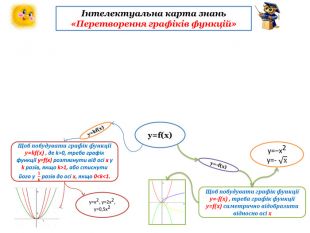
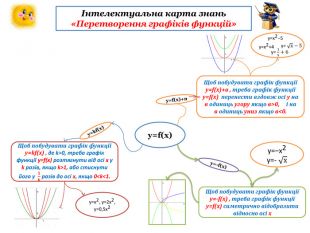
-В ході пояснення кожен учень має заповнити
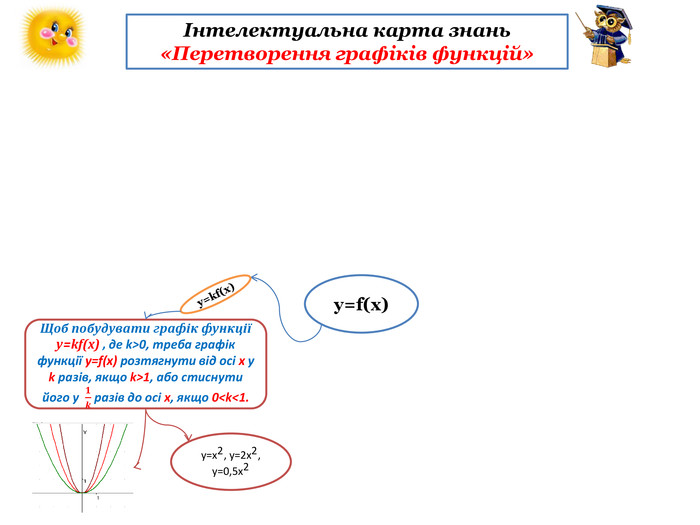
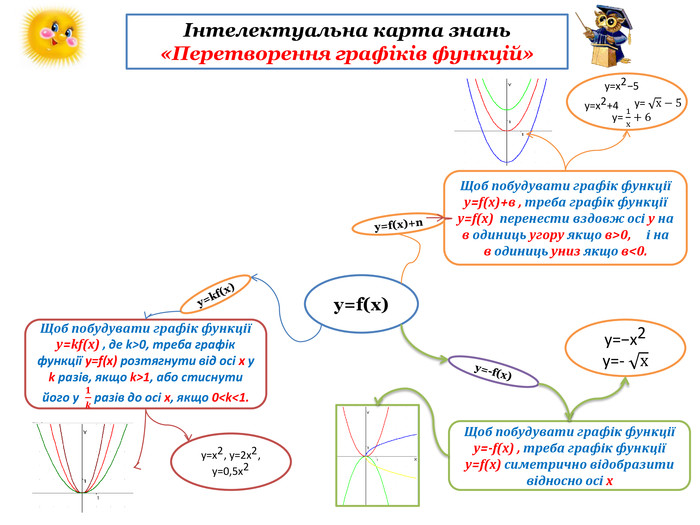
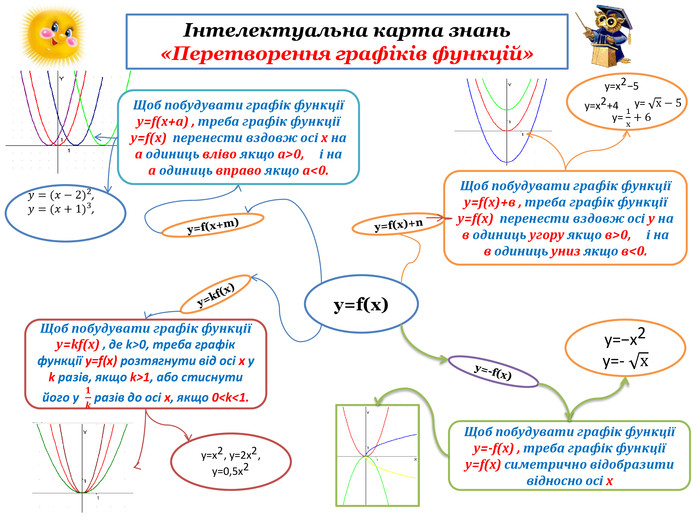
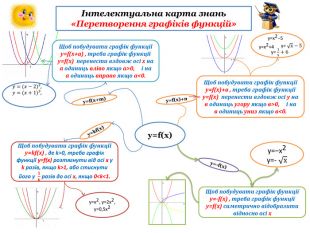
інтелектуальну карту знань «Перетворення графіків функцій»
(Додаток 1). Шаблони карти знань учні отримують від вчителя.
Демонстрація результатів досліджень
-
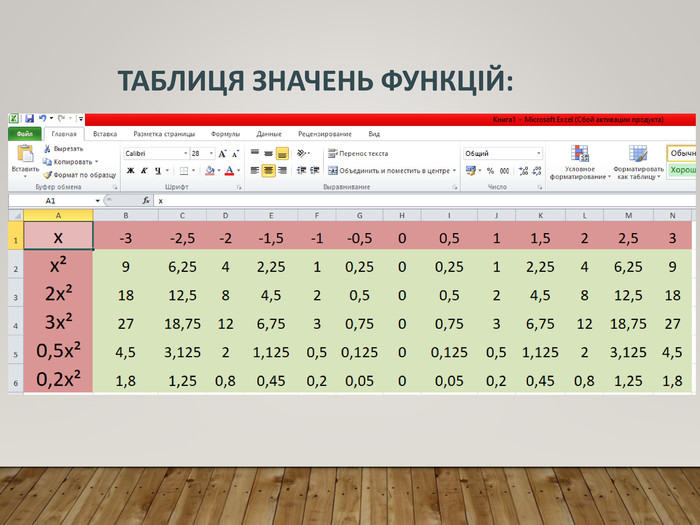
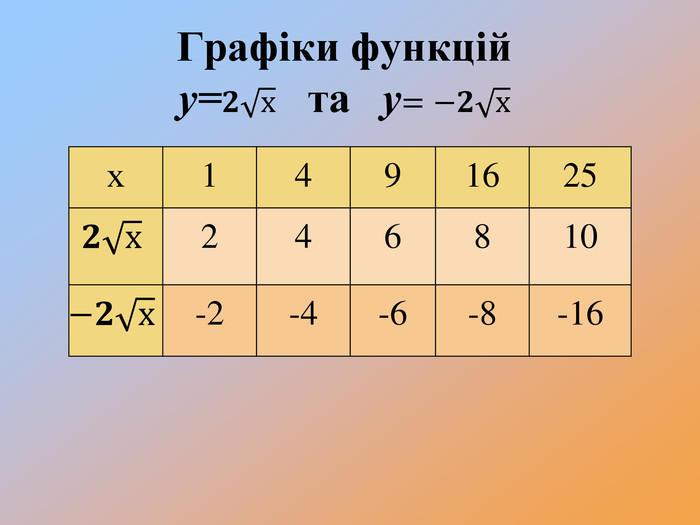
Перетворення
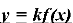 Формулювання правила (із записом у карту знань):
Формулювання правила (із записом у карту знань):

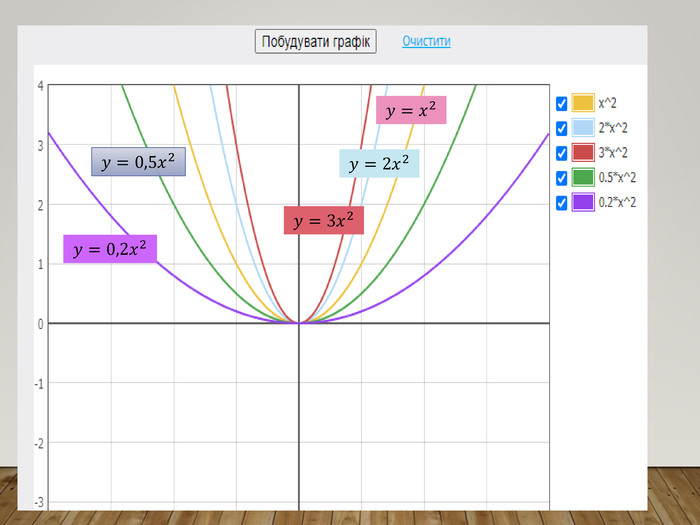
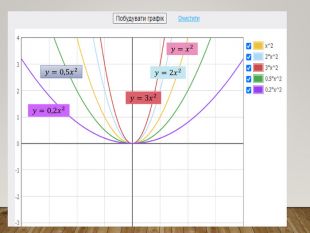
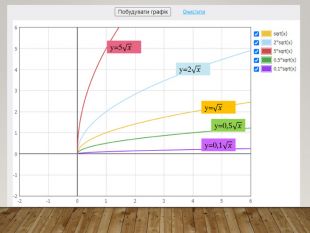
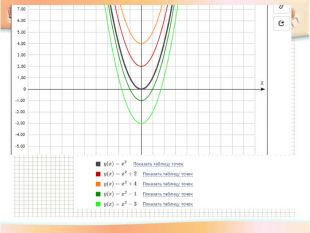
Обговорення результатів побудови:
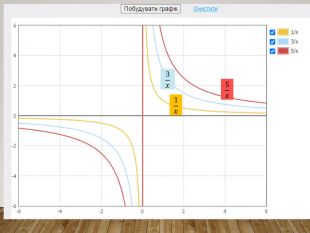
-Чи змінилася форма графіка функції? ( Ні, але графіки стають стислими або розлогими)
Зверніть увагу: якщо графік віддаляється від осі абсцис, говорять, що він розтягується від осі абсцис; якщо графік наближається до осі абсцис, то говорять, що він стискається до осі абсцис.
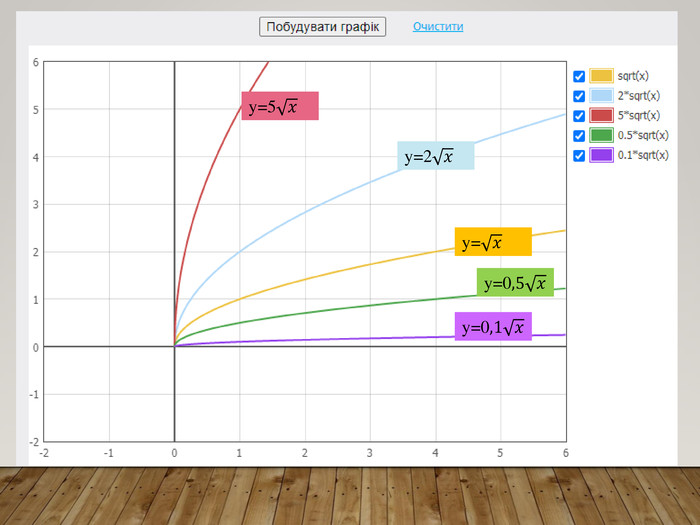
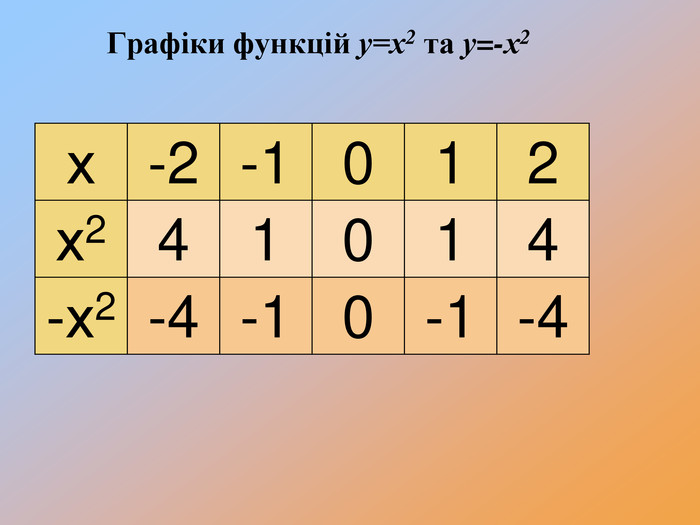
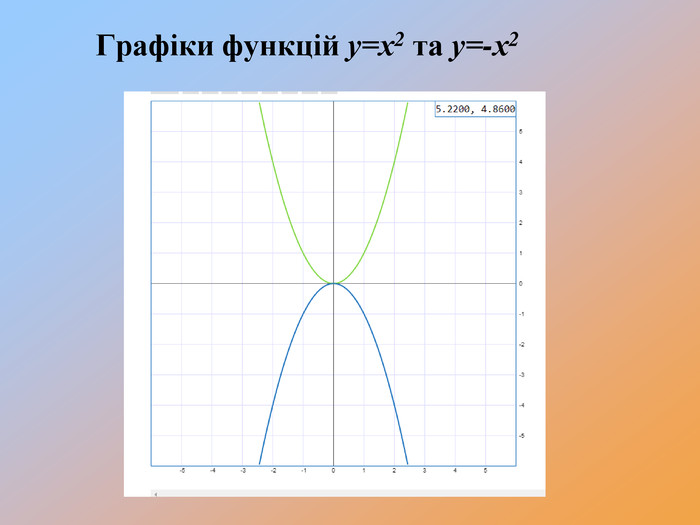
-
Перетворення
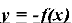
Формулювання правила (із записом у карту знань):

Обговорення результатів побудови:
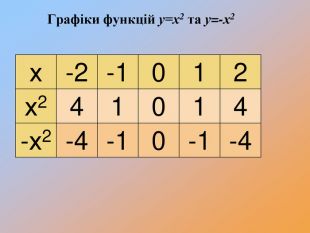
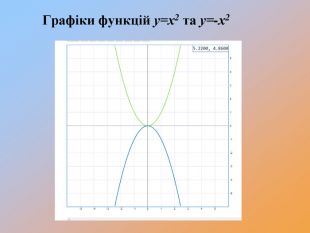
-Чи змінилася форма графіка функції?
-Чи будуть графіки симетричними відносно осі абсцис?
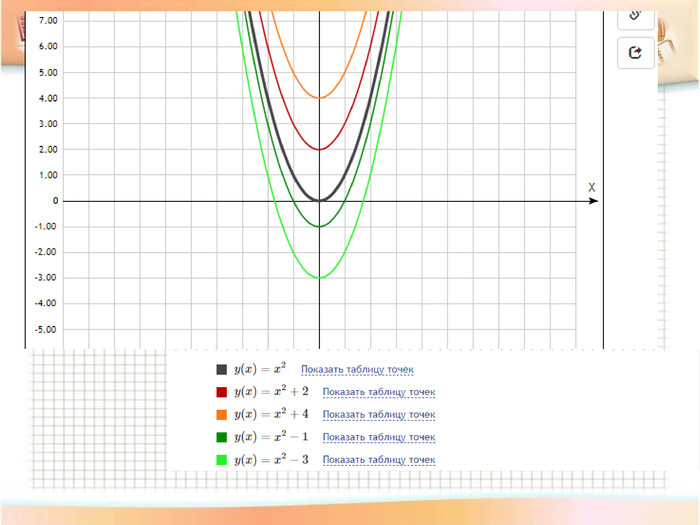
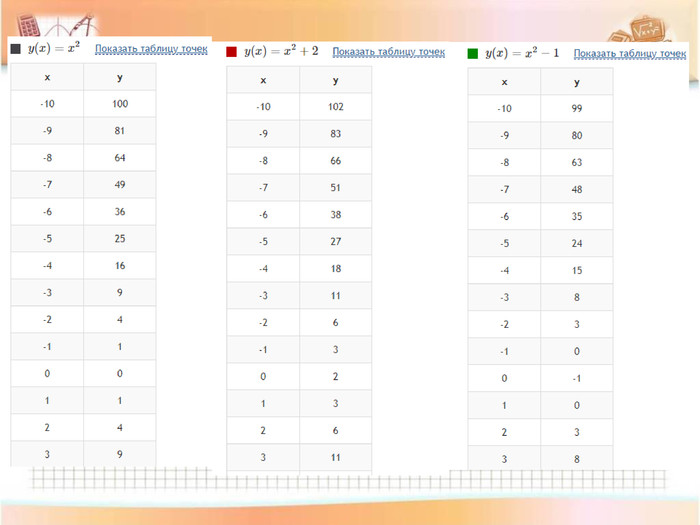
-
Перетворення
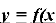 )+в
)+в
(Поки Данило готується- В зошиті побудуємо 3 системи координат)
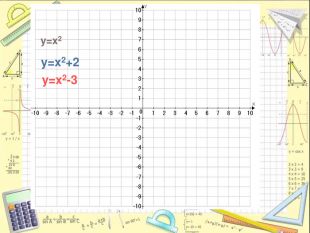
Висновок

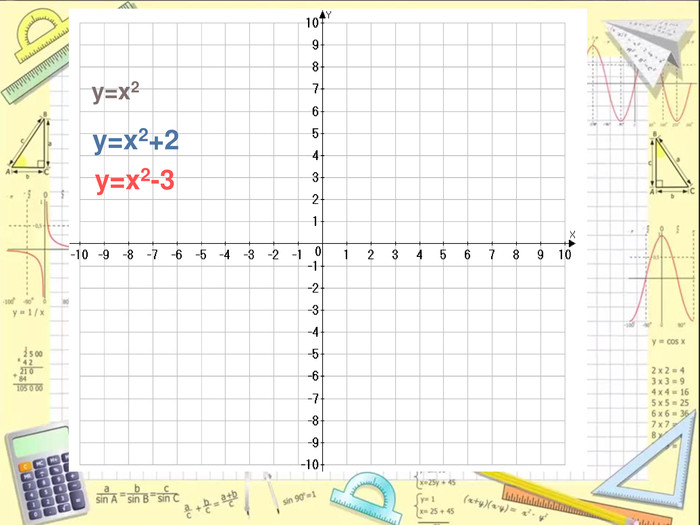
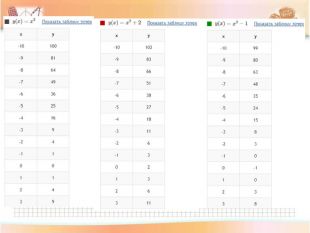
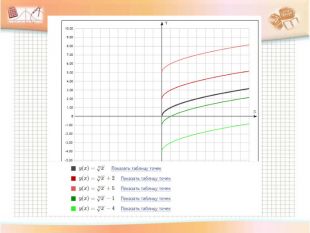
Обговорення результатів побудови. Учні роблять висновки даючи відповіді на запитання:
-Чи змінилася форма графіка функції?
- Куди змістився графік, коли до значення функції додали додатне число і на скільки одиниць?
-Куди змістився графік, коли до значення функції додали від’ємне число і на скільки одиниць?
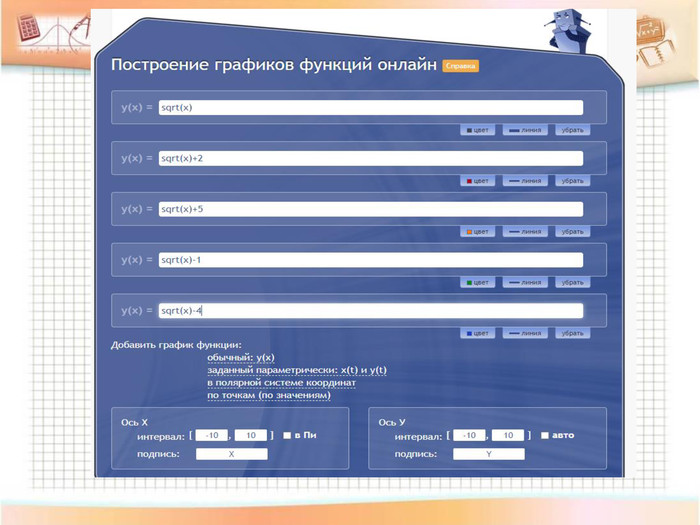
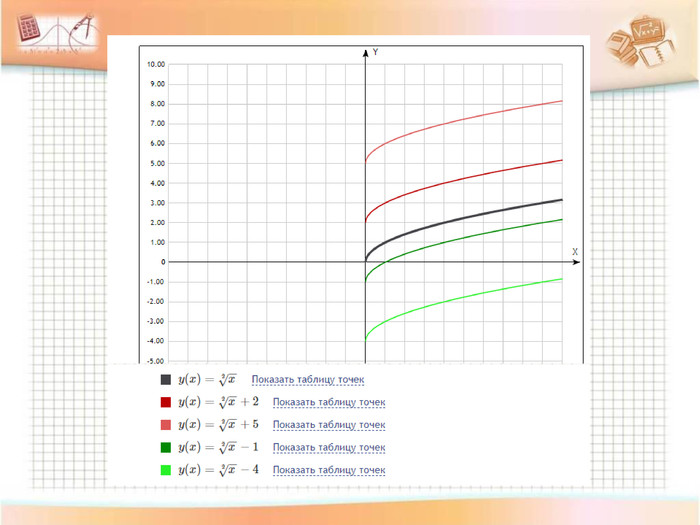
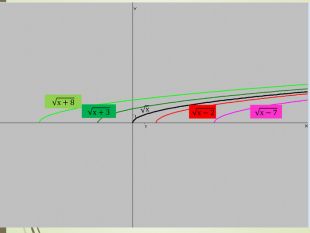
4.Перетворення ![]() )
)

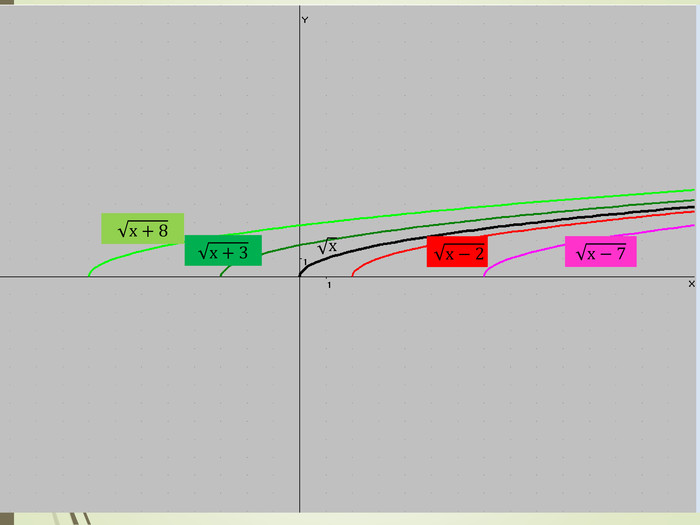
Обговорення результатів побудови та формулювання правила (із записом у карту знань):
- Що змінилось при побудові графіків?
- Чи змінилася форма графіка функції?
- Куди змістився графік, коли до значення аргументу додали додатне число і на скільки одиниць?
- Куди змістився графік, коли до значення аргументу додали від’ємне число і на скільки одиниць?
VІ. УСВІДОМЛЕННЯ НОВИХ ЗНАНЬ І ВМІНЬ
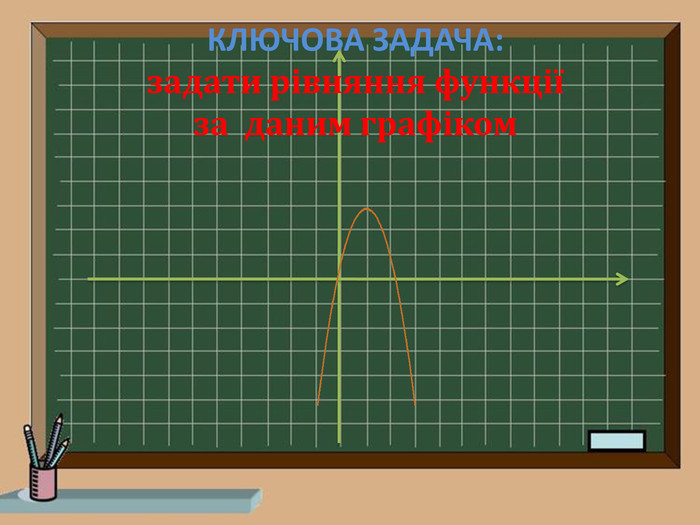
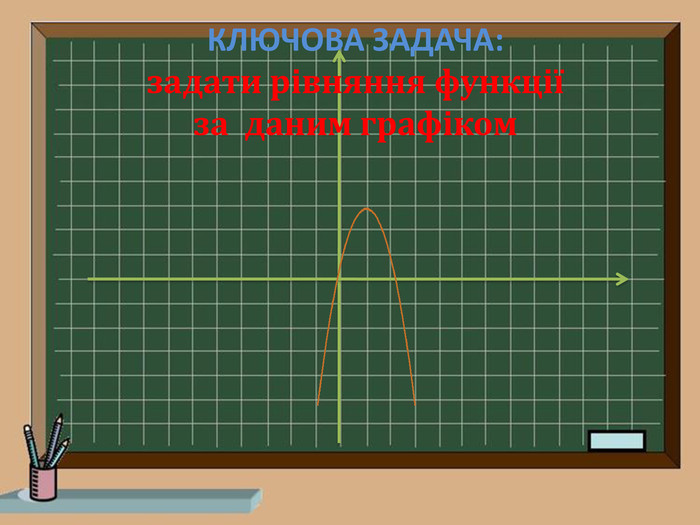
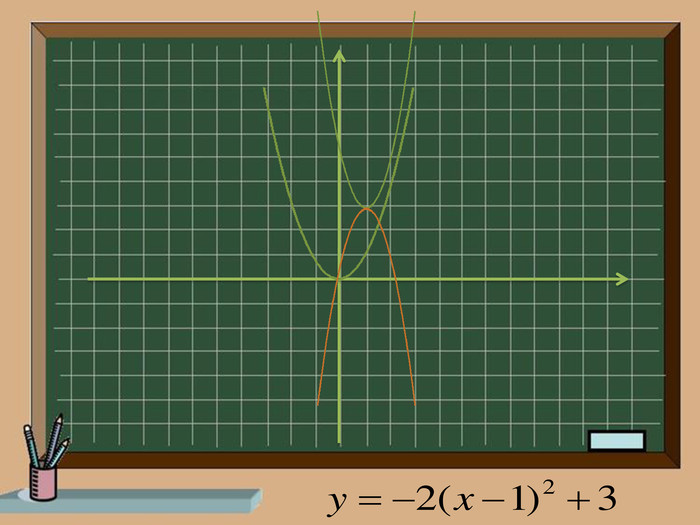
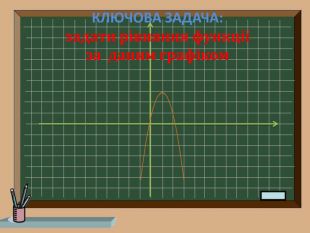
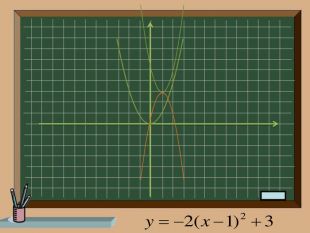
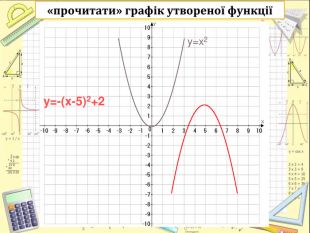
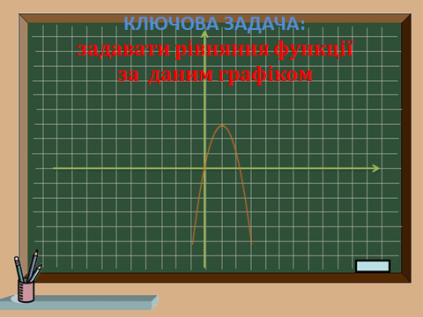
Ключова задача!!!
-Яку функцію взято за основу?
-Які перетворення здійснено?
-Запишемо рівняння функції
VII. ПІДСУМОК УРОКУ
VIII. ДОМАШНЄ ЗАВДАННЯ
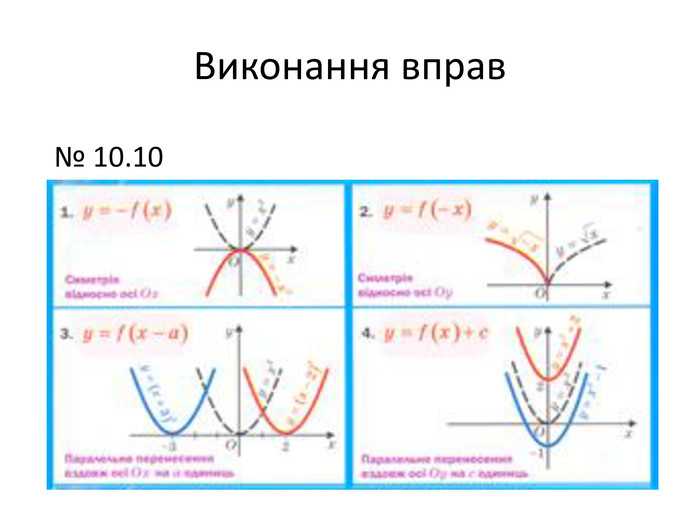
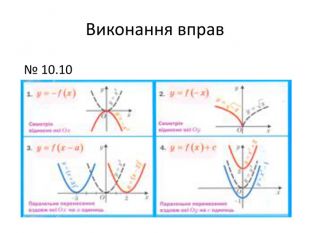
Вправ3. «Геометричні перетворення графіків функцій».
Завдання вправи в GOOGLE Клас.


про публікацію авторської розробки
Додати розробку