Перпендикуляр і похила

Підготувалавчитель математики, школи І – ІІІ ступенів №286 міста Києва. Слободенюк Ніла Василівна. Перпендикулярі похила. Київ 2020

МЕТА уроку:сформувати поняття перпендикуляра до площини, похилої, проекції похилої на площину; відстань від точки до площини; установити взаємозв’язок між довжинами похилих, проведених з однієї точки до площини, і довжинами їхніх проекцій на площину.розвивати критичне мислення, логіку, увагу, навчати самоконтролю та взаємоконтролю, комунікативні компетентності;виховувати відповідальності, наполегливість у досягненні мети, віру у свої сили, інтерес до математики через ознайомлення з відомостями з історії геометрії.

Тип уроку: засвоєння нових знань. Технології: інформаційні технологіїОбладнання: мультимедийная программа Microsoft Power. Point, засоби онлайн зв’язку. Сайти: https://quizizz.com; https://www.liveworksheets.com

Мотивація навчальної діяльності

«Єдиний шлях, який веде до знань, - це діяльність» Бернард Шоу

У – уміння С – самостійність П – працелюбність І – інтуіція Х - хоробрість

Сьогодні на уроці:«Пригадай, ти це знаєш!»«Зрозумій, це просто!»«Виконай, у тебе вийде!»«Переконайся, ти навчився!»

Актуалізація опорних знань: «Пригадай, ти це знаєш!»

Означення: aa. SAFNDH Пряма називається перпендикулярною до площини, якщо вона перпендикулярна до будь-якої прямої, що належить цій площині. Кут між прямими дорівнює 90˚. Як називаються такі прямі? Дайте означення прямої, перпендикулярної до площини. Відповідь: Перпендикулярні.

qpa,a p, р a q, q , 3. Сформулюйте ознаку перпендикулярності прямої і площини. a. Якщо пряма перпендикулярна до двох прямих, що перетинаються і належать площині, то вона перпендикулярна до цієї площини.p ∩ q = O

Мотивація навчальної діяльностіСвіт, що нас оточує, – це світ геометрії. Тож давайте його пізнавати!Пізанська вежа. Опори мосту

Вітрильник. Будівельний рівень. Мотивація навчальної діяльності

Балет. Телескоп. Мотивація навчальної діяльності

Усвідомлення нового матеріалу: «Зрозумій, це просто!»

«Аналогія, напевно, має частку в усіх відкриттях, але в деяких вона має левову частку» Дьйорд Пойя ПРАВИЛО-ОРІЄНТИР вибір і формулювання твердження В у планіметрії, перегляд та аналіз цього твердження;перехід за допомогою «словника перекладача»;формулювання твердження про існування та достовірність твердження А в стереометрії.

ПЛАНІМЕТРІЯ Допоміжне твердження В Площина Простір Точка Пряма Пряма Площина СТЕРЕОМЕТРІЯ Твердження А, що вивчається. СЛОВНИЧОК - ПЕРЕКЛАДАЧ

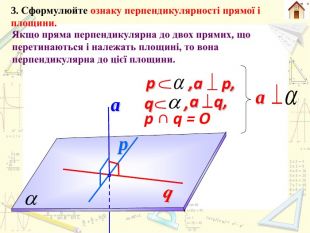
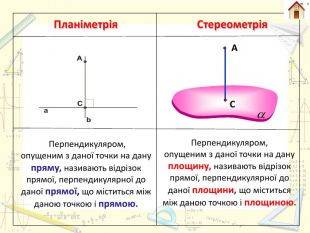
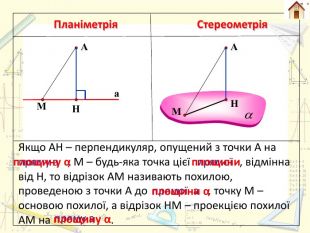
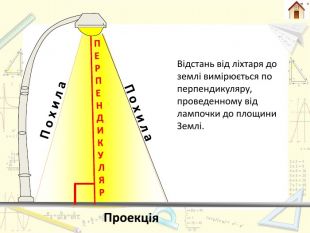
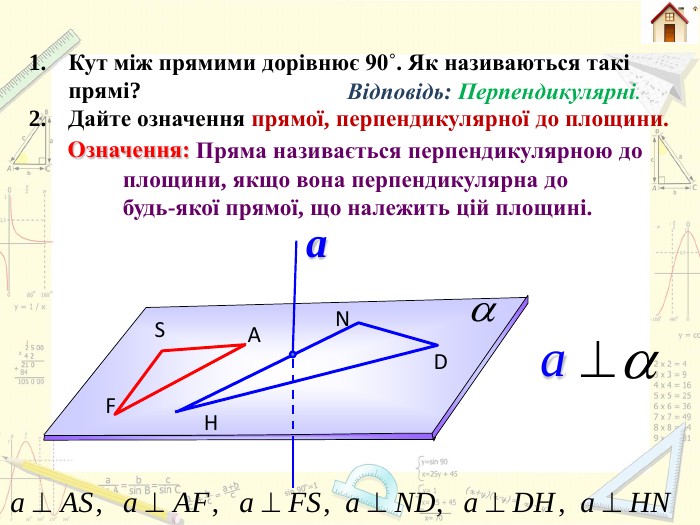
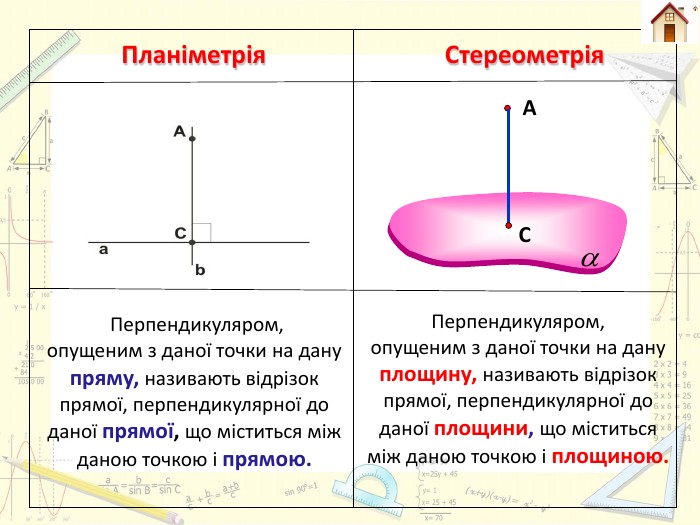
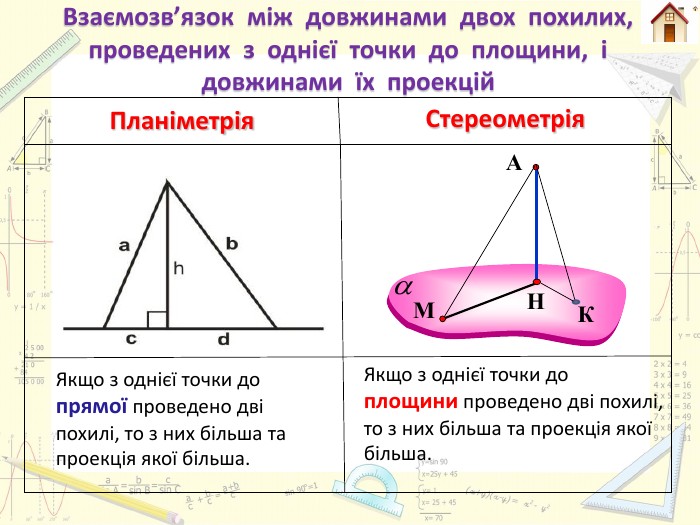
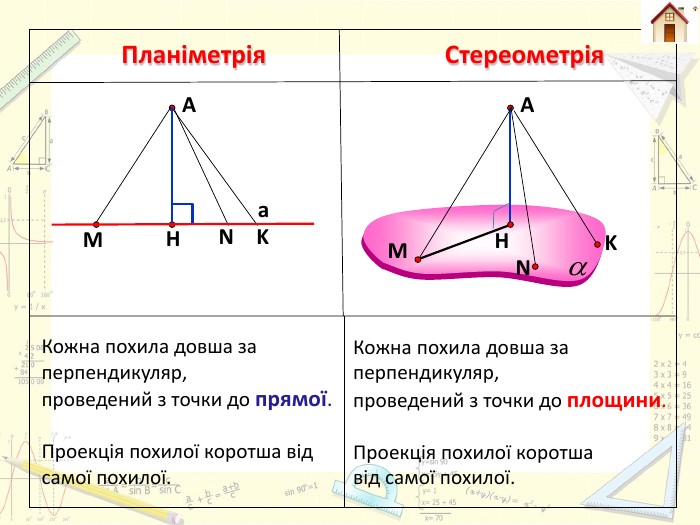
Планіметрія. Стереометрія Перпендикуляром, опущеним з даної точки на дану пряму, називають відрізок прямої, перпендикулярної до даної прямої, що міститься між даною точкою і прямою. Перпендикуляром, опущеним з даної точки на дану площину, називають відрізок прямої, перпендикулярної до даної площини, що міститься між даною точкою і площиною. СА

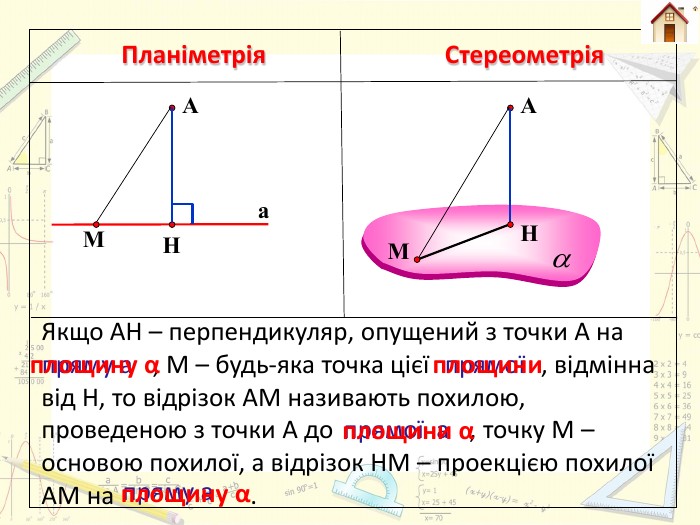
Планіметрія. Стереометрія. Якщо АН – перпендикуляр, опущений з точки А на , М – будь-яка точка цієї , відмінна від Н, то відрізок АМ називають похилою, проведеною з точки А до , точку М – основою похилої, а відрізок НМ – проекцією похилої АМ на . НАа. АНММпряму апрямоїпрямої апряму аплощину α площиниплощини αплощину α

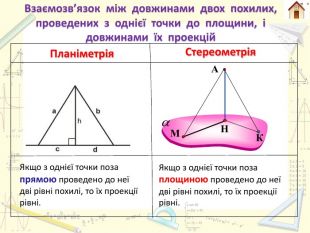
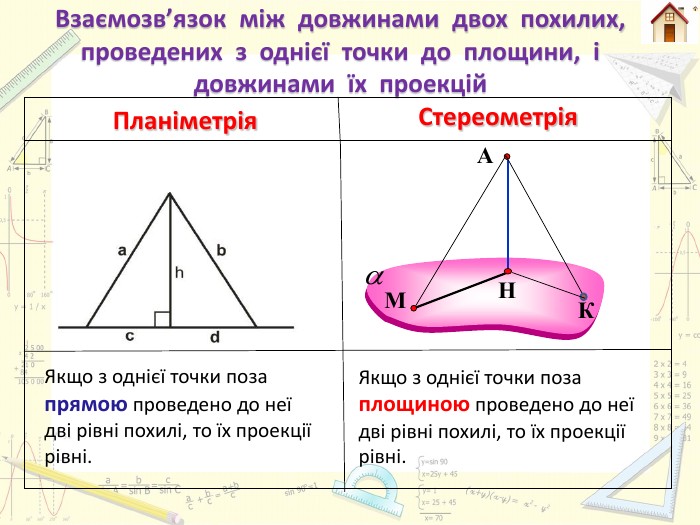
Планіметрія. Стереометрія. Якщо з однієї точки поза прямою проведено до неї дві рівні похилі, то їх проекції рівні. Якщо з однієї точки поза площиною проведено до неї дві рівні похилі, то їх проекції рівні. Взаємозв’язок між довжинами двох похилих, проведених з однієї точки до площини, і довжинами їх проекцій. НМАК

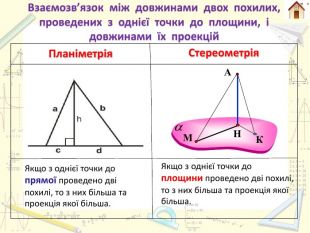
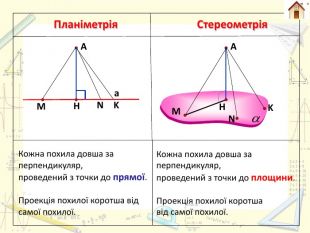
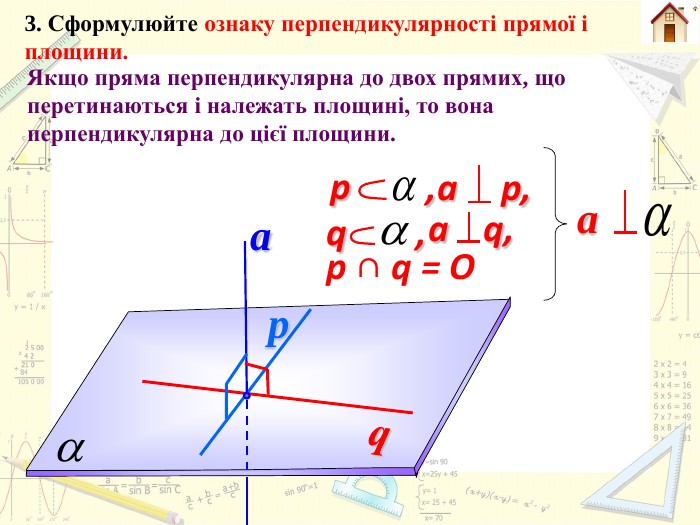
Планіметрія. Стереометрія. Якщо з однієї точки до прямої проведено дві похилі, то з них більша та проекція якої більша. Якщо з однієї точки до площини проведено дві похилі, то з них більша та проекція якої більша. Взаємозв’язок між довжинами двох похилих, проведених з однієї точки до площини, і довжинами їх проекцій. НМКА

Планіметрія. Стереометрія. НАа. МАНМКожна похила довша за перпендикуляр, проведений з точки до прямої. Проекція похилої коротша від самої похилої. Кожна похила довша за перпендикуляр, проведений з точки до площини. Проекція похилої коротша від самої похилої. N KNK

Відстань від ліхтаря до землі вимірюється по перпендикуляру, проведенному від лампочки до площини Землі. П о х и л а П о х и л а ПЕРПЕНДИКУЛЯР Проекція

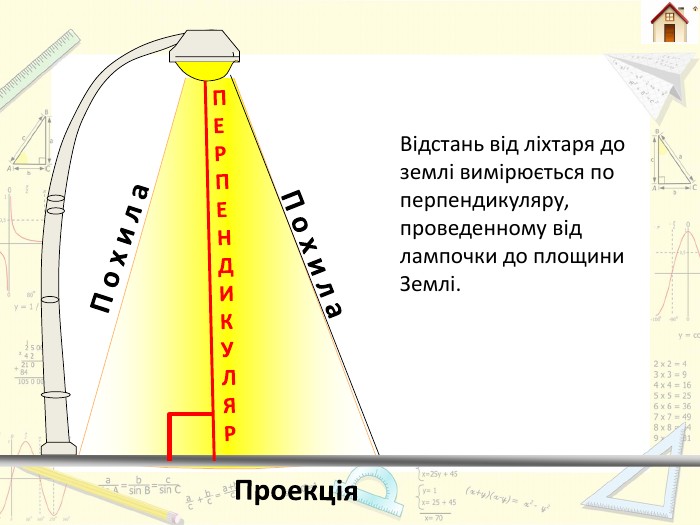
Властивості перпендикуляра й похилої застосовуються на практиці. Наприклад, якщо встановлюють щоглу на радіостанції, то стяжки беруть рівної довжини. Нижні кінці їх закріпляють на однакових відстанях від основи щогли. Це сприяє стійкості щогли. Властивості перпендикуляра й похилої«Головне значення перпендикуляра – це його роль у техніці і у всьому нашому вжитку» О. Д. Александров

Закріплення здобутих знань: «Виконай, у тебе вийде!»

«Виконай, у тебе вийде!»Розв’язування елементарних задач на похилу та її проекцію на площину зводиться до розв’язування прямокутного трикутника, сторонами якого є похила, її проекція на площину і перпендикуляр до площини. Якщо такого трикутника немає на малюнку, то, щоб його утворити, проводимо допоміжні відрізки.

Задача 1. Знайдіть довжину похилої, якщо довжина перпендикуляра дорівнює 6 см, а проекції похилої на площину – 8 см. А В С α Розв’язання: З ∆АВС (∟В = 90°) за теоремою Піфагора маємо: АС2=ВС2+ ВА2; АС2= 82+62; АС2=64+36;АС2=100;АС = 10см. Відповідь: АС=10 см. Розв’язування задач

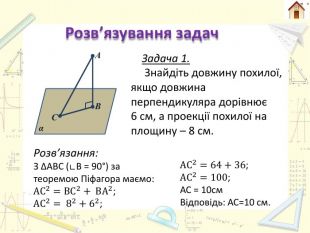
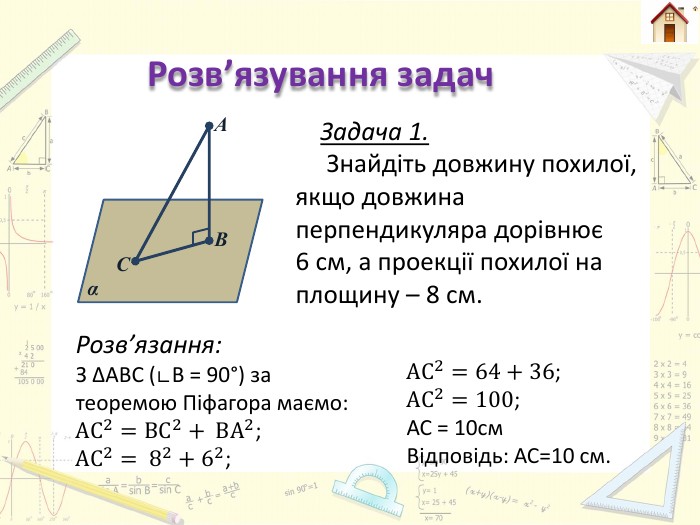
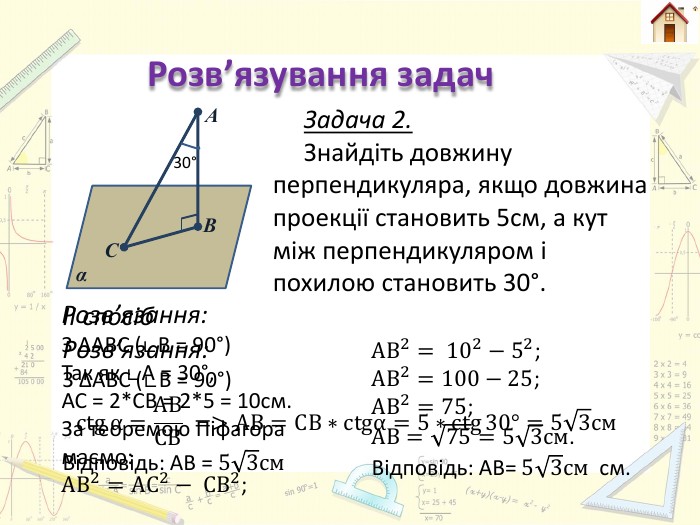
А В С α Розв’язування задач Задача 2. Знайдіть довжину перпендикуляра, якщо довжина проекції становить 5см, а кут між перпендикуляром і похилою становить 30°.30°Розв’язання: З ∆АВС (∟В = 90°)Так як ∟А = 30°, АС = 2*СВ = 2*5 = 10см. За теоремою Піфагора маємо: АВ2=АС2− СВ2;  АВ2= 102−52;АВ2=100−25;АВ2=75;АВ=75=53см. Відповідь: АВ= 53см  см. ІІ спосіб. Розв’язання: З ∆АВС (∟В = 90°)ctgα=ABCB =>AB=CB∗ctgα=5∗ctg30°=53см. Відповідь: АВ = 53см 

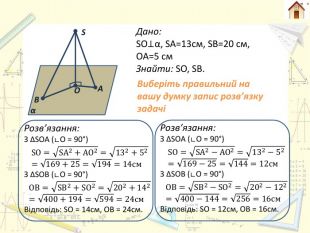
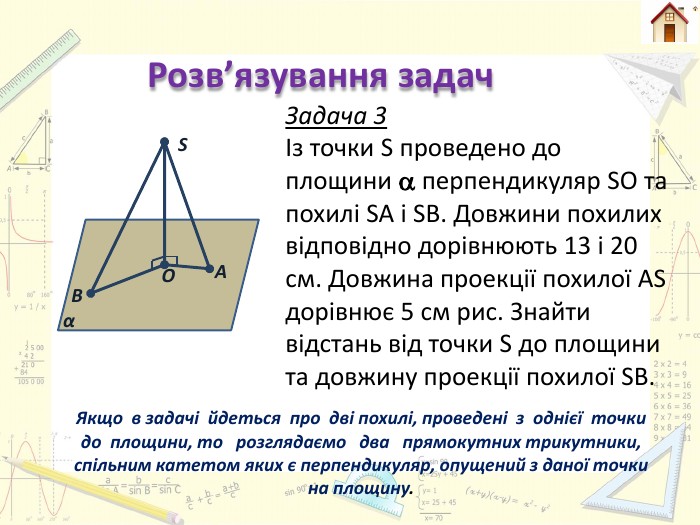
Розв’язування задач. S B α О A Задача 3Із точки S проведено до площини  перпендикуляр SO та похилі SA і SB. Довжини похилих відповідно дорівнюють 13 і 20 см. Довжина проекції похилої AS дорівнює 5 см рис. Знайти відстань від точки S до площини та довжину проекції похилої SB. Якщо в задачі йдеться про дві похилі, проведені з однієї точки до площини, то розглядаємо два прямокутних трикутники, спільним катетом яких є перпендикуляр, опущений з даної точки на площину.

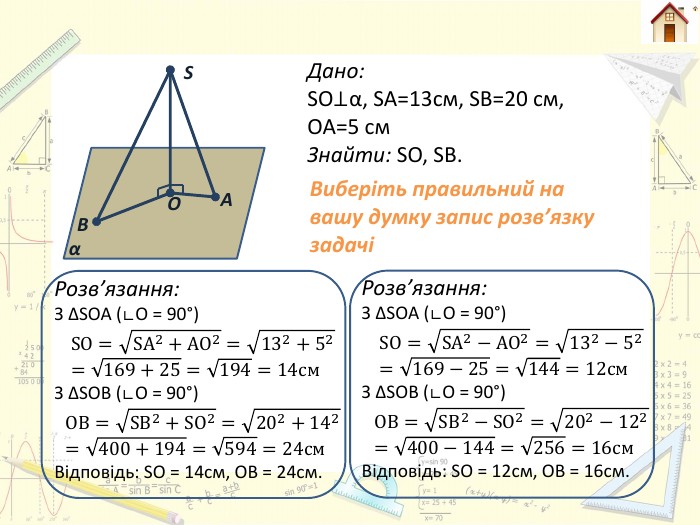
S B α О A Дано: SO⊥α, SA=13см, SB=20 см,OA=5 см. Знайти: SO, SВ. Виберіть правильний на вашу думку запис розв’язку задачіРозв’язання: З ∆SOA (∟O = 90°)SO=SA2−AO2=132−52=169−25=144=12см. З ∆SOB (∟O = 90°)OB=SB2−SO2=202−122=400−144=256=16см. Відповідь: SO = 12см, ОВ = 16см.  Розв’язання: З ∆SOA (∟O = 90°)SO=SA2+AO2=132+52=169+25=194=14см. З ∆SOB (∟O = 90°)OB=SB2+SO2=202+142=400+194=594=24см. Відповідь: SO = 14см, ОВ = 24см.  

А В α О С Розв’язування задач Задача 4. З точки до площини проведені дві похилі, які дорівнюють 10 см і 17 см, а їх проекції відносяться, як 2:5. Знайдіть відстань від даної точки до площини.

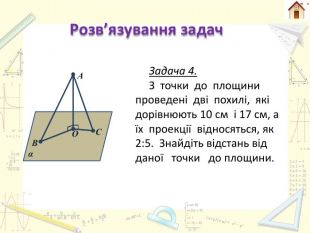
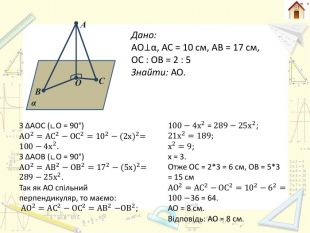
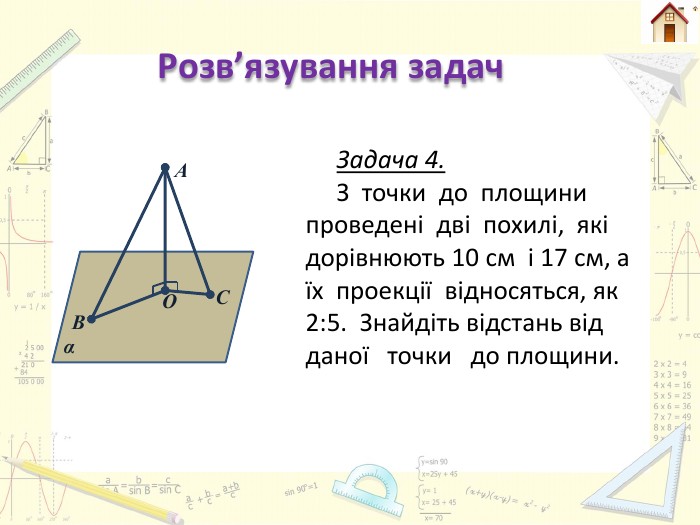
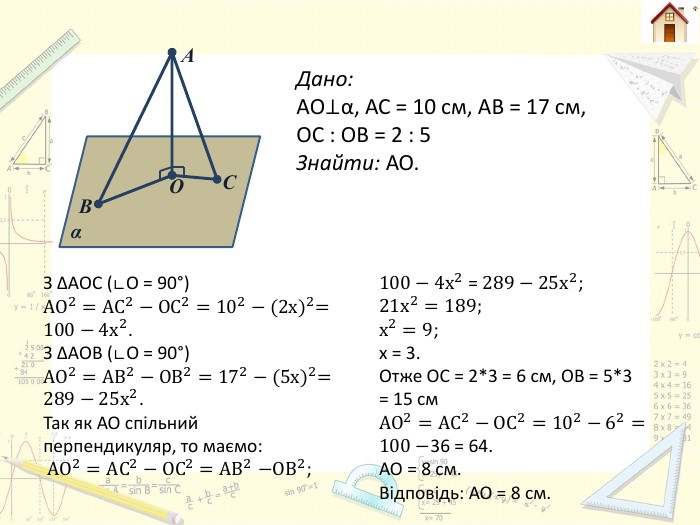
А В α О С Дано: АO⊥α, АС = 10 см, АВ = 17 см,ОС : ОВ = 2 : 5 Знайти: АО. З ∆АOС (∟O = 90°)АО2=АС2−ОС2=102−(2х)2=100−4х2. З ∆АOВ (∟O = 90°)АО2=АВ2−ОВ2=172−(5х)2=289−25х2. Так як АО спільний перпендикуляр, то маємо: АО2=АС2−ОС2 =АВ2−ОВ2; 100−4х2 = 289−25х2;21х2=189;х2=9;х = 3. Отже ОС = 2*3 = 6 см, ОВ = 5*3 = 15 см. АО2=АС2−ОС2=102−62=100−36 = 64. АО = 8 см. Відповідь: АО = 8 см. 

Підсумок уроку: «Переконайся, ти навчився!»

Перейдіть за посиланням та виконайте завдання:https://www.liveworksheets.com/2-ac125015lzІнтерактивна вправа: «Перпендикуляр і похила»

«Якщо запастись терпінням і проявити старанність, то посіяні зерна знань обов’язково дадуть добрі паростки» Леонардо да Вінчі

Домашнє завдання: Прошу вас перейти за посиланнямjoinmyquiz.com та ввести код доступу59074360 і пройти тест.https://quizizz.com/admin/quiz/5fb282572b8ac0001bd1ca92

Задача для розумників Задача З даної точки до площини проведено три рівні похилі довжиною 14 см. Відстані між кінцями похилих дорівнюють 9 см. Знайдіть відстань від даної точки до площини.

Оце так я, оцемолодець!Ну, я звісно не лінувався, але й дуже не старався…Скажу знову, що я нічого не зрозумів. Рефлексія

Дякую за урок!