Перша і друга ознаки рівності трикутників
Тема. Перша і друга ознаки рівності трикутників
Мета: закріпити знання учнів про зміст та способи застосування теорем, що виражають першу і другу ознаки рівності трикутників, для розв'язування задач на доведення рівності трикутників; виробити вміння добирати аргументацію і доводити рівність трикутників із використанням першої і другої ознак рівності трикутників, а також використовувати доведення рівності трикутників для доведення рівності відрізків, кутів і для доведення паралельності прямих.
Тип уроку: закріплення знань, відпрацювання вмінь.
Обладнання: набір демонстраційного креслярського приладдя, таблиця № 13 «Ознаки рівності трикутників».
Хід уроку
І. Організаційний етап
ІІ. Перевірка домашнього завдання
- Задачу № 360 перевіряємо за готовим розв'язком. Це можна зробити після виконання математичного диктанту, на етапі мотивації навчальної діяльності.
- Для перевірки засвоєння учнями змісту теорем, що виражають першу і другу ознаки рівності трикутників, проводимо математичний диктант.
Математичний диктант № 8
Варіант 1 [2]
- У трикутниках KNO і PQT [ABC і DEF] рівні сторони KN [АВ] і PQ [DE] і кути К [А] і Р [D]. Яка ще умова має виконуватися, щоб ці трикутники були рівні за першою ознакою?
- У трикутниках ABC і DEF [MPQ і KLT] сторони АВ і ВС [MP і PQ] дорівнюють відповідно сторонам DE і EF [KL і LT]. Трикутники ці не рівні. Що можна сказати про кути В і Е [Р і L]?
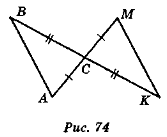
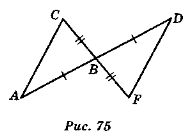
- Доведіть рівність трикутників ABC і МКС (рис. 74) [ABC і DBF (рис. 75)].
- У трикутниках BCD і MPQ [MPQ і KLT] кути В і D [М і Q] рівні відповідно кутам М і Q [К і Т]. Трикутники не рівні. Що випливає звідси відповідно до другої ознаки рівності трикутників?
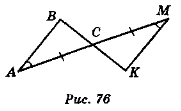
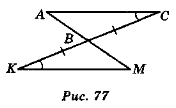
- Доведіть рівність трикутників ABC і МКС (рис. 76) [ABC і МВК (рис. 77)].
III. Формулювання мети і завдань уроку, мотивація навчальної діяльності учнів
Спираючись на аналіз результатів перевірки домашнього завдання, вчитель разом із учнями формулює дидактичну мету уроку: закріпити знання змісту теорем, що виражають першу і другу ознаки рівності трикутників і виробити вміння застосовувати їх при розв'язуванні задач.
IV. Актуалізація опорних знань і вмінь учнів
Усні вправи
- Відомо, що пари трикутників на рис. 78 рівні. Запишіть відповідні рівності.
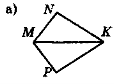
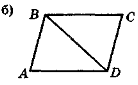
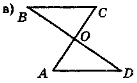
Рис. 78
- Які елементи трикутників MNK і DEF мають бути рівними, щоб виконувалася рівність трикутників за першою ознакою?
- Знайдіть на рис. 79 пари рівних відрізків або кутів, використовуючи вивчені властивості найпростіших геометричних фігур.
|
а) О — середина АВ; |
б) AC = DB; |
в) AD = ВС; |
|
|
г) ОА — бісектриса - |
д)
|
||
|
є)
|
ж) а
|
||
Рис. 79
- Доведіть рівність трикутників за другою ознакою (рис. 80, а).
-
Дано: AD = CF,
 1 =
1 = 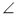 2,
2, 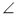 3 =
3 = 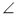 4 (рис. 80, б). Доведіть рівність трикутників за другою ознакою.
4 (рис. 80, б). Доведіть рівність трикутників за другою ознакою.
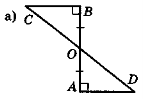
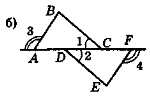
Рис. 80
V. Відпрацювання навичок
Методичний коментар
Для успішної реалізації основної дидактичної мети уроку бажано розв'язати якомога більше різнорівневих задач на доведення та обчислення, що передбачають:
1) пряме застосування першої і другої ознак рівності трикутників;
2) застосування ознак рівності трикутників у зміненій ситуації;
3) застосування доведення рівності трикутників для доведення рівності відрізків та кутів.
Письмові вправи
- Відомо, що трикутники ABC і НТО рівні. На сторонах АВ і НТ відкладено рівні відрізки АК і НМ відповідно. Доведіть рівність трикутників АСК та НОМ.
-
У трикутнику ABC
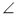 A =
A = 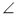 C. На сторонах АВ і АС відкладено рівні відрізки AM і СК відповідно. Знайдіть довжину відрізка АК, якщо CM = = 14 см.
C. На сторонах АВ і АС відкладено рівні відрізки AM і СК відповідно. Знайдіть довжину відрізка АК, якщо CM = = 14 см.
- У трикутнику ABC AB = BC. Бісектриса кута В перетинає сторону АС у точці К. Знайдіть кут між прямими АС і ВК.
-
У трикутниках ABC і АКС
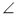 1 =
1 =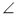 2,
2, 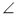 3 =
3 =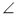 4. Знайдіть кут К, якщо
4. Знайдіть кут К, якщо 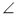 B = = 110° (рис. 81).
B = = 110° (рис. 81).
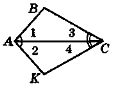
Рис. 81
-
На рис. 82
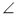 A =
A = 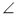 F,
F, 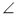 1 =
1 = 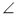 2, AD = FC. Доведіть рівність трикутників ABC і FED.
2, AD = FC. Доведіть рівність трикутників ABC і FED.
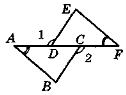
Рис. 82
-
У трикутнику ABC на рівних сторонах АС і ВС позначено точки М і Е відповідно, причому
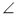 CAE =
CAE = 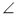 CBM. Доведіть, що АЕ = ВМ .
CBM. Доведіть, що АЕ = ВМ .
- На рис. 83 трикутники ABC і КСВ рівні. Доведіть рівність трикутників АОВ і КОС.
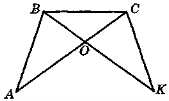
Рис. 83
- № 368, 369, 370 (див. підручник).
Зазначимо, що вже на даному уроці можна починати формувати в учнів навички усвідомлених розумових дій, які потрібні для розв'язування геометричних задач, а саме — навички виконувати прямі та зворотні міркування, що супроводжують пошук розв'язку геометричних задач (так звані аналітичний та синтетичний способи міркувань).
VI. Підсумки уроку
Доведіть, що ВС = РК (рис. 84). Складіть план розв'язання задачі.

Рис. 84
VIII. Домашнє Завдання
- § 12, теореми 10 і 11 (перша і друга ознаки рівності трикутників) — вивчити зміст і доведення.
- Письмові вправи: № 367, 371, 374.
- § 9—11 — повторити теоретичний матеріал, № 376.


про публікацію авторської розробки
Додати розробку