Перші відомості про математичну статистику. Вибірка. Гістогра¬ма. Середнє значення, мода і медіана вибірки.

Тема. Перші відомості про математичну статистику. Вибірка. Гістогра­ма. Середнє значення, мода і медіана вибірки.

Мета. Дати учням уявлення про математичну статистику, формування понять: вибірка, гістограма, середнє значення, мода і медіана ви­бірки.

І.  Перевірка домашнього завдання

1. Перевірити правильність виконання домашніх завдань за за­писами на дошці, зробленими до початку уроку.

Вправа № 300

  , .

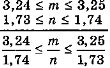
Отже, .

Відповідь. 1,87 ± 0,01.

Вправа № 303

х + у = 21,37 + 9,832 = 31,202 31,20

х – у = 21,37 – 9,832 = 11,538 11,54

ху = 21,37 ∙ 9,832 = 210,10984 210,1

.

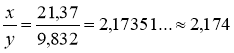2. Фронтальна бесіда.

Запитання до класу

1. Сформулюйте правило підрахунку цифр для додавання та віднімання наближених значень.
2. Сформулюйте правило підрахунку цифр для множення та ділення наближених значень.
3. Як виконують наближені обчислення з точним урахуван­ням похибок?

II. Самостійна робота

I варіант

1. Відомо, що 3,22 ≤ а ≤ 3,26 і 1,14 ≤ b ≤ 1,2. Знайдіть наближене значення і межу абсолютної похибки суми а + b і частки 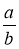.              (6 балів)
2. Знайдіть за правилами підрахунку цифр суму, різницю, добуток і частку наближених значень х = 34,12 і у = 19,6.                                          (6 балів)

II варіант

1. Відомо, що 3,22 < а < 3,26 і 1,14 < b < 1,2. Знайдіть наближене значення і межу абсолютної похибки різниці а - b і добутку аb.              (6 балів)
2. Знайдіть за правилами підрахунку цифр суму, різницю, добуток і частку наближених значень х = 2,05 і у = 1,2.                                          (6 балів)

Відповіді.

I варіант. 1. а + b = 4,41 ± 0,05, . 2. х + у = 53,7; х – у = 14,5;

хy = 669; .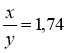

II варіант. 1. а – b = 2,07 ± 0,05, аb = 3,79 ± 0,12. 2. х + у = 3,3; х – у = 0,9;

ху = 2,5; .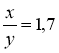

III. Формування в учнів уявлення про математичну статистику; формування понять вибірки, гістограми, середнього значення, моди і медіани вибірки

Статистика — наука, яка збирає, обробляє і вивчає різні дані, пов'язані з масовими явищами, процесами, подіями. Предметом вивчення статистики є вивчення кількісної сторони цих явищ.

Математична статистика — розділ математики, присвячений ма­тематичним методом систематизації, обробки та дослідження ста­тистичних даних для наукових і практичних висновків.

Звернемося до прикладів.

Приклад 1. Дев'ятикласники однієї школи написали конт­рольну роботу. З них 16 ви­конали завдання на 10-12 балів, 31 — на 7-9 балів, 33 — на 4-6 балів, 7 — на 1-3 бали.

Це статистичні дані, кіль­кісні характе-ристики прове­деної контрольної роботи. їх можна подати у вигляді табл. 25.

Таблиця 25

Наочно зобразити ці дані можна за допомогою стовпчастої діаграми, яку в статистиці називають гістограмою (рис. 153).

Ми розглянули приклад, який охоплює (досліджує) 87 об'єктів (учнів).

Статистика, як правило, має справу з масовими явищами, які охоплюють тисячі або й мільйони досліджуваних об'єктів.

Приклад 2. Виробникам жіночого одягу треба знати, скільки одягу треба випускати того чи іншого розміру. Як це з'ясувати? Опита­ти всіх жінок неможливо, тому роблять вибірку: опитують вибір­ково кілька десятків чи сотень людей. Припустимо, що опитали 50 жінок, розміри їхнього одягу такі:

44, 50, 48, 48, 52, 50, 52, 48, 46, 50, 50, 52, 54, 46, 48, 48, 54, 52, 46, 50, 52, 48, 46, 50, 52, 50, 48, 50, 54, 48, 48, 50, 52, 46, 52, 56, 50, 44, 56, 50, 52, 48, 56, 54, 46, 54, 50, 56, 54, 60.

Це — вибірка з 50 значень (даних). Для зручності дані запи­шемо у вигляді таблиці, у першому рядку якої вкажемо розмір одягу, а в другому — частоту, з якою зустрічаються у вибірці ті чи інші її значення (табл. 26). Такі таблиці називають частот­ними.

Таблиця 26

Відносною частотою значення вибірки називають відношен­ня його частоти до числа усіх значень.

Побудуємо таблицю відносної частоти (табл. 27).

Таблиця 27

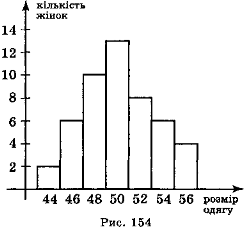За табл. 27 можна побудувати гістограму (рис. 154). Вона наочно показує, яку частину одягу бажано випускати того чи іншого розміру.

Звичайно, одержані таким способом висновки не точні, а на­ближені, але для потреб практики цього досить.

Кожна вибірка характе­ризується центральними тенденціями: середнім зна­ченням, модою і медіаною.

Середнє значення вибір­ки — це середнє арифме­тичне її значень.

Мода вибірки — те її зна­чення, яке трапляється най­частіше.

Медіана вибірки — це чис­ло, яке «поділяє навпіл» упорядковану сукупність усіх значень вибірки.

У прикладі 2 середнє значення вибірки:

.

Медіана даної вибірки дорівнює 50, бо число 50 поділяє впо­рядковану вибірку навпіл.

Мода вибірки дорівнює 50, бо 50 зустрічається найчастіше.

Виконання вправ   

Вправи № 308, 310, 311 (б).

IV. Домашнє завдання

§ 65, контрольні запитання 33-37 (с. 276 підручника); № 307, 309, 311 (а).

V. Підведення підсумків уроку

Запитання до класу

1. Що таке математична статистика?
2. Що таке гістограма? Наведіть приклади.
3. Що таке вибірка? Частота вибірки?
4. Назвіть центральні тенденції вибірки.
5. Що таке мода, медіана, середнє значення вибірки?