Первісна. Основна властивість первісних.
Тема: Первісна. Основна властивість первісних. Таблиця первісних.
Мета уроку:
Сформулювати означення первісної, основну властивість первісних, розглянути таблицю первісних деяких основних функцій;
розвивати вміння розв’язувати завдання на основі отриманих знань;
виховувати інтерес до вивчення точних наук.
Цілі:
засвоїти означення первісної;
використовувати таблицю первісних при розв’язуванні вправ;
знаходити значення первісної в заданій точці.
Формувати:
математичну компетентність ( уміння застосовувати вивченні поняття
та формули до розв’язування вправ );
спілкування державною мовою (уміння ставити запитання і
розпізнавати проблему; міркувати, робити висновки на основі поданої
інформації ).
Тип уроку: засвоєння нових знань.
Хід уроку
- Організаційний етап
- Актуалізація опорних знань
Що ми називаємо похідною функції?
Сформулюйте означення похідної функції ![]() у точці
у точці ![]()
Похідною функції ![]() у точці
у точці ![]() називають число, яке дорівнює границі відношення приросту функції
називають число, яке дорівнює границі відношення приросту функції ![]() у точці
у точці ![]() до відповідного приросту аргументу за умови, що приріст аргументу прямує до нуля
до відповідного приросту аргументу за умови, що приріст аргументу прямує до нуля
![]()
 Пригадаємо таблицю похідних деяких основних функцій
Пригадаємо таблицю похідних деяких основних функцій
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Як називається операція знаходження похідної функції?
(Операція знаходження похідної функції ![]() називається диференціюванням функції
називається диференціюванням функції ![]() )
)
Якщо функція має похідну в точці, як називають таку функцію?
(Якщо функція ![]() має похідну в точці
має похідну в точці ![]() , то цю функцію називають диференційовною в точці
, то цю функцію називають диференційовною в точці ![]() )
)
Якщо функція диференційовна в кожній точці області визначення, як
називають таку функцію?
(Якщо функція ![]() диференційовна в кожній точці області визначення, то така функція називається диференційовною)
диференційовна в кожній точці області визначення, то така функція називається диференційовною)
Знаючи закон руху матеріальної точки ![]() , як можемо знайти закон зміни швидкості
, як можемо знайти закон зміни швидкості ![]() ?
?
![]()
- Мотивація навчальної діяльності:
Бесіда з учнями.
Кожна математична дія має обернену: додавання – віднімання, множення – ділення. Яка дія є оберненою до операції диференціювання?
Проблемне питання:
Чи можемо визначити закон руху ![]() , якщо відомо
, якщо відомо ![]() ?
?
Так, необхідно відновити функцію за її похідною. Знаходження функції за її похідною називають інтегруванням.
- Сприйняття та усвідомлення нового матеріалу.
Первісна
Означення
Функцію ![]() називають первісною функцією функції
називають первісною функцією функції ![]() на проміжку
на проміжку ![]() , якщо для всіх
, якщо для всіх ![]() виконується рівність
виконується рівність ![]()
Наприклад:
|
|
Первісна для |
|
|
|
|
Первісна для |
? (запитати учнів, до якої функції на їх думку буде первісною ця функція) |
|
|
|
Первісна для |
? (запитати учнів, до якої функції на їх думку буде первісною ця функція) |
|
Основна властивість первісної
Знайдіть похідну для функцій:
![]() //
// ![]()
![]() //
// ![]()
Скільки первісних має функція ![]()
(Безліч)
Теорема (основна властивість первісної)
Якщо функція ![]() є первісною функції
є первісною функції ![]() на проміжку
на проміжку ![]() та
та ![]() – довільне число, то функція
– довільне число, то функція ![]() також є первісною функції
також є первісною функції ![]() на проміжку
на проміжку ![]() .
.
|
|
Будь-яку первісну функції
|
![]() – загальний вигляд первісних функції
– загальний вигляд первісних функції ![]() на проміжку
на проміжку ![]() .
.

Беручи до уваги основну властивість первісних, як можемо отримати графіки будь-яких двох первісних для даної функції?
(Паралельним перенесенням уздовж осі ординат)
Графіки будь-яких первісних для заданої функції одержують один з одного паралельним перенесенням уздовж осі ![]() .
.
Сукупність усіх первісних ![]() на проміжку
на проміжку ![]() називається невизначеним інтегралом:
називається невизначеним інтегралом:![]()
Таблиця первісних деяких функцій
|
Функція |
Первісна функції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- Осмислення нового матеріалу.
№1 Установіть, чи є функція ![]() первісною функції
первісною функції ![]() :
:
-

-
 на проміжку
на проміжку 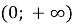
-

-

Розв’язання:
Так як проміжок не вказаний, то мається на увазі проміжок ![]()
![]() на проміжку
на проміжку ![]() , так як
, так як ![]()
-
 на проміжку
на проміжку 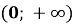
На проміжку ![]() ,
, ![]()
![]()
![]()
![]() на проміжку
на проміжку ![]() так як
так як ![]()
![]() на проміжку
на проміжку ![]() , так як
, так як ![]()
№2 Чи є функція ![]() первісною функції
первісною функції ![]() на проміжку:
на проміжку:
-
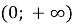 ;
;
-
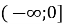 ;
;
Розв’язання:
Так як ![]() і
і ![]() не визначені для
не визначені для ![]() :
:
- Так (нуль не включається у проміжок);
- Ні (нуль включається у проміжок);
№3 Знайдіть загальний вигляд первісних функцій:
-
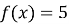
-
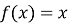
-
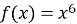
-

-
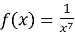 на проміжку
на проміжку 
-
 на проміжку
на проміжку 
-
 на проміжку
на проміжку 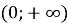
Розв’язання:
№4 Для функції ![]() знайдіть первісну, графік якої проходить через указану точку:
знайдіть первісну, графік якої проходить через указану точку:
Розв’язання:
Знайдемо первісну:
![]()
Підставимо значення функції в заданій точці та знайдемо значення ![]() :
:
![]()
![]()
Відповідь: ![]()
Знайдемо первісну:
![]()
Підставимо значення функції в заданій точці та знайдемо значення ![]() :
:
![]()
![]()
![]()
Відповідь: ![]()
Знайдемо первісну:
![]()
Підставимо значення функції в заданій точці та знайдемо значення ![]() :
:
![]()
![]()
Відповідь: ![]()
№5 Для функції ![]() знайдіть на проміжку
знайдіть на проміжку ![]() первісну
первісну ![]() , яка набуває даного значення у вказаній точці:
, яка набуває даного значення у вказаній точці:
Розв’язання:
Знайдемо первісну:
![]()
Підставимо значення функції в заданій точці та знайдемо значення ![]() :
:

![]()
![]()
Відповідь: ![]()
Знайдемо первісну:
![]()
Підставимо значення функції в заданій точці та знайдемо значення ![]() :
:
![]()
![]()
![]()
Відповідь: ![]()
Знайдемо первісну:
![]()
Підставимо значення функції в заданій точці та знайдемо значення ![]() :
:
![]()
![]()
![]()
Так як на проміжку ![]()
![]()
Відповідь: ![]()
- Підсумок уроку
Бліцопитування.
- Що ми називаємо диференціюванням функції?
- Що ми називаємо інтегруванням функції?
- Сформулюйте означення первісної функції
- Сформулюйте основну властивість первісної
- Що ми називаємо невизначеним інтегралом?
- Домашнє завдання
|
Опрацювати §8, опрацювати
|
Істер О.С. |


про публікацію авторської розробки
Додати розробку


