Матеріали до уроків "Завдання для розвитку творчих компетентностей учнів на уроках алгебри в 7 класі"
Практичні завдання для розвитку творчого потенціалу учнів на уроках алгебри у 7 класі
Дніпровський ліцей № 129
Дніпровської міської ради
Завдання для розвитку творчих
компетентностей учнів на уроках
алгебри в 7 класі
Учитель математики
Дніпровського ліцею № 129
Правденко В.Г.
Зміст
- Вступ
1.Лінійні рівняння з однією змінною.
1.1. Розв’язування лінійних рівнянь
1.2 . Розв’язування задач з допомогою лінійних рівнянь.
2. Цілі вирази.
2.1. Степінь і його властивості.
2.2. Одночлени.
2.3. Многочлени.
3.Розкладання многочленів на множники.
3.1. Квадрат двочлена.
3.2.Різниця квадратів.
3.3. Застосування кількох способів розкладання на множники.
4.Системи лінійних рівнянь.
4.1. Системи лінійних рівнянь.
4.2. Розв’язування задач з допомогою систем лінійних рівнянь.
Вступ
Епоха, що настала – епоха змін, інновацій. епоха інтелекту, диктує свої умови життя.
Якісно нові зміни в суспільстві переконують. що найбільшою цінністю є неповторна людська особистість з її нахилами, вподобаннями, обдаруваннями.
Одним з основних завдань української школи є виховання творчої особистості учня. Підвищення інтелектуального потенціалу нації і розвиток творчої особистості є однією найактуальніших цілей освіти.
А одним із напрямків реалізації творчої потреби дитини в умовах шкільного навчання є застосування в навчальному процесі творчих вправ, що сприяє глибокому і міцному засвоєнню матеріалу, розвитку особистості кожного школяра. Адже коли високий інтелект поєднується з високим рівнем креативності, творча людина краще адаптована до середовища, активна, емоційно врівноважена. незалежна тощо.
1.Лінійні рівняння з однією змінною
1.1. Розв’язування лінійних рівнянь
Розв’яжіть рівняння :
-
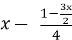 –
– 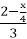 = 2;
= 2;
-
 ;
;
-
 = 3 –
= 3 – 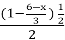 ;
;
-
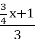 -
- 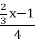 = х + 3.
= х + 3.
![]() :
:
-
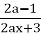 = 1;
= 1;
-
 +
+  = с;
= с;
-
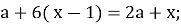
-
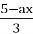 =
= 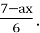
Укажіть при яких значеннях параметра а рівняння мають нескінченну множину розв’язків:
- 6(ах – 1) – а = 2(а + х) – 7;
- 0,5(5х – 1) = 4,5 – 2а(х – 2).
При яких значеннях параметра рівняння ах – 4 = 3х має корінь, що дорівнює 8?
1.2.Розвязування задач з допомогою лінійних рівнянь
1. Перша труба заповнює басейн за половину того часу, за який друга труба наповнює ![]() цього басейну. Друга труба наповнює басейн на 6 годин довше, ніж перша труба. Скільки часу заповнює басейн кожна труба окремо?
цього басейну. Друга труба наповнює басейн на 6 годин довше, ніж перша труба. Скільки часу заповнює басейн кожна труба окремо?
2. Пішохід , який поспішав на електричку, пройшов за першу годину 3,5 км і зрозумів, що рухаючись з такою швидкістю, він запізниться на 1 годину. Тому решту шляху пішохід рухався зі швидкістю 5км/год і прибув за 30хв до відправлення елктрички. Визначте який шлях треба було пройти пішоходу.
3. Туристи за першу годину пройшли 3 км. Якби вони продовжили рухатись з тією ж швидкістю, то запізнилися б до місця збору на 40хв. Тому вони збільшили швидкість на ![]() і прийшли до місця збору за 45хв до назначеного часу. Яку відстань пройшли туристи до місця збору і за який час?
і прийшли до місця збору за 45хв до назначеного часу. Яку відстань пройшли туристи до місця збору і за який час?
4. Екскаватор мав вирити траншею певної довжини. За перший день він вирив 305% довжини всієї траншеї, за другий - на 10% більше, ніж за перший, а за третій – решту 111 км. Знайти довжину траншеї.
5. Сплав міді і олова має масу 12 кг і містить 45% міді. Скільки олова треба додати до цього сплаву, щоб отримати новий сплав, що містить 40% міді?
6. Білка за 16 хвилин приносить горіх до гнізда. Яку відстань вона при цьому пробігає, якщо з горіхом вона біжить зі швидкістю 3м/с, а без горіха – 5м/c?
10. Із учнів, що писали роботу, 30% отримали 11балів, 40% - 8балів, 8 учнів отримали 6балів, решта – 4бали. Середній бал дорівнював 3,9. Скільки учнів отримали кожну із оцінок?
2.Цілі вирази
2.1. Степінь і його властивості.
1. Розв’яжи рівняння:
а)![]() = -1; б)
= -1; б)![]() = 0; в) 5
= 0; в) 5![]() = 0; г)
= 0; г)![]() = 1.
= 1.
2. Обчислити: ![]() ·
·![]() , де n – натуральне число.
, де n – натуральне число.
3. Знайти значення виразу: а) ![]() ; б)
; б) ![]()
4. На скільки ![]() менше, ніж 9?
менше, ніж 9?
5. Запиши числа ![]() ,
, ![]() ,
, ![]() в порядку зростання.
в порядку зростання.
6. Що більше: ![]() чи
чи ![]() ?
?
7. Що більше: ![]() чи
чи ![]()
8. Довести, що ![]() +
+![]() ділиться на 33.
ділиться на 33.
9. Довести, що ![]() +
+ ![]() ділиться на 37
ділиться на 37
10. Довести, що значення числового виразу
![]() +
+![]() +
+![]() ділиться на 10.
ділиться на 10.
2.2 Одночлени
1.Виконати дії:
1) (- 0,4![]() ) (- 0,8
) (- 0,8![]() );
);
2) (- ![]() ) (
) (![]() x
x![]() );
);
3) (-8![]() ) (-
) (-![]() ).
).
2.При якому значенні n правильна рівність?
1) ![]() = 32
= 32![]() ;
;
2) ![]() · 100 = 4
· 100 = 4![]() ;
;
3) ![]() =-
=- ![]() ;
;
4)![]() · 0,001 =
· 0,001 = ![]()
3.Мило має форму прямокутного паралелепіпеда. За тиждень користування
його розміри зменшилися в 2 рази. У скільки разів зменшився об’єм мила?
4. Об’єм кулі знаходять за формулою:
V = ![]() π
π![]() , де r – радіус кулі. Як зміниться об’єм кулі, якщо радіус збільшити в 4 рази?
, де r – радіус кулі. Як зміниться об’єм кулі, якщо радіус збільшити в 4 рази?
2.3 Многочлени
1. Спростити вираз ( n– натуральне число):
а) ![]() (
(![]() - 1) -
- 1) - ![]() (
( ![]() -
- ![]() );
);
б) ![]() (
( ![]() - 4) -
- 4) - ![]() (
( ![]() - 4a +1);
- 4a +1);
в) ![]() (
(![]() (
(![]() +
+ ![]() (
( ![]() - x +1) ) ).
- x +1) ) ).
2. Обчислити ( n – натуральне число, n![]() ):
):
а) (12 · ![]() - 8·
- 8· ![]() + 4·
+ 4· ![]() ) ÷ (4·
) ÷ (4·![]() );
);
б) (36 ·![]() - 8·
- 8· ![]() -
- ![]() ) ÷
) ÷![]() .
.
3. Довести, що якщо 2( a + 1) ( b + 1) = ( a + b) ( a + b +2) , то ![]() +
+ ![]() = 2.
= 2.
4. Довести,що сума трьох послідовних чисел ділиться на 6.
5. Учні 7 класу прийшли до театру. В антракті всі вони пішли до буфету. Кожен хлопчик купив пиріжок, кожна дівчинка - булочку. Якби кожна дівчинка купила пиріжок,а кожен хлопчик – булочку, то вони разом витратили на 50грн менше. Пиріжок дорожче булочки на 10грн. Кого було більше: хлопців чи дівчат і на скільки більше?
6.В банці було 3л спирту. Із неї відлили X л спирту, а долили таку ж кількість води. Потім, коли спирт і вода змішались повністю, із банки відлили X л суміші. Скільки літрів спирту залишилося в банці?
7. У двозначному числі число десятків втроє більше, ніж одиниць. Якщо від цього числа відняти число. записане тими ж цифрами, але в зворотньому порядку, то отримаємо 36. Знайди це число.
8. Дано чотири послідовних числа. Що більше: добуток найменшого і найбільшого із цих чисел чи добуток решти двох чисел і на скільки більше?
3.Розкладання многочленів на множники
3.1. Квадрат двочлена.
1.Виконай піднесення до квадрата:
![]() ;
;
![]() ;
;
3) ![]() ;
;
4) ![]() .
.
2.Розклади на множники:
1) ![]() - 2
- 2![]() ;
;
2) ![]()
3) 4ab (a + b) – ![]()
3. Довести, що при кожному натуральному n значення виразу
![]() - 2(
- 2(![]() + 2) (
+ 2) (![]() - 2) +
- 2) + ![]() ділиться на 16.
ділиться на 16.
4. Ціле число при діленні на 7 дає в остачі 3. Яку остачу при діленні на 7 дає квадрат цього числа?
3.2. Різниця квадратів.
1.Доведіть, що
![]() =
= ![]()
2. Доведіть тотожність
( a + b)![]() =
= ![]() -
- ![]() якщо a – b = 1
якщо a – b = 1
3. Розв’яжіть рівняння:
![]() =
= ![]() + x
+ x
4. Виконайте дії:
1) ![]() )
) ![]()
2) ![]() .
.
5.Довести, що при будь-якому натуральному n число
![]() -
- ![]() ділиться на 8.
ділиться на 8.
6. Розкласти на множники:
1) 9![]() – 1;
– 1;
2) 4 – 25![]() ;
;
3) 9![]() –
– ![]()
4) 49 ![]() – 9
– 9![]()
7. Довести, що при будь-якому натуральному n значення виразу:
1) ![]() -
- ![]() ділиться на 12;
ділиться на 12;
2) ![]() -
- ![]() ділиться на 7.
ділиться на 7.
3.3.Застосування кількох способів розкладання на множники.
1.Розв’язати рівняння:
-
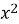 – 4x + x - 4 = 0;
– 4x + x - 4 = 0;
- y ( y – 5 ) – 5 ( 5 – y ) = 0;
-
2
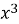 - 3
- 3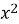 + 2x – 3 = 0.
+ 2x – 3 = 0.
2. Розкласти на множники:
-
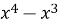
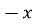 + 1; 7)
+ 1; 7)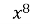 +
+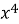 + 2;
+ 2;
-
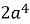 + 2
+ 2 2
2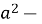 2a; 8)
2a; 8) 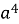 + 4;
+ 4;
-
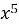 -
- 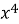 - 2
- 2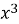 + 2
+ 2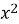 + x – 1; 9)
+ x – 1; 9) 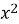 + x – 12;
+ x – 12;
-
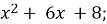 10)
10) 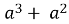 – 12;
– 12;
-
2
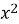 + 14x + 24; 11)
+ 14x + 24; 11) 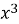 - 7x + 16.
- 7x + 16.
-
3
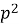 + 27 p + 54;
+ 27 p + 54;
3. Якщо a ≠ 0, або b ≠ 0, то значення виразу 5![]() - 6ab + 5
- 6ab + 5![]() додатнє. Довести.
додатнє. Довести.
4. Довести, що при будь-якому x: ( x – 3) ( x – 5 ) + 2 ![]() 0/
0/
4. Системи лінійних рівнянь
1.Розв’яжіть систему:
1) 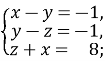 2)
2)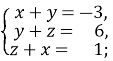 3)
3)![]()
4)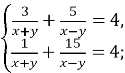 5)
5)![]() 6)
6)![]()
7)
2.Розв’яжіть задачу:
1) Сума цифр двозначного числа дорівнює12,а різниця числа одиниць і числа десятків ф цьому числі в 12разів менше самого числа. Знайдіть це число.
2) Сума цифр двозначного числа 12.Число написане тими ж цифрами , але в зворотньому порядку, на 54 більше поданого числа. Знайдіть це число.
3) Якщо задумане число розділити на суму його цифр, то в частці отримаємо 4, а в остачі 3. Якщо від задуманого числа відняти подвоєну суму його цифр,то отримаємо 25.Яке число було задумане.
4) В три посудини налита вода. Якщо половину води із першого посудини перелити в другий, потім ![]() частину води, що була в другій посудині, перелити в третій, і нарешті,
частину води, що була в другій посудині, перелити в третій, і нарешті, ![]() частину води, що була в третій посудині, перелити в перший, то в кожній стане по 6л. Скільки води було в кожній посудині до переливання?
частину води, що була в третій посудині, перелити в перший, то в кожній стане по 6л. Скільки води було в кожній посудині до переливання?
5) Написали два числа. Якщо перше число збільшити на 30%, а друге зменшити на 10%, то їх сума збільшиться на 6. Якщо ж перше число зменшити на 10%, а друге зменшити на 20%, то їх сума зменшиться на 16. Які числа були записані?
6)Із пункту А в пункт Б одночасно виїхали два мотоциклісти. Коли через 1,5год перший мотоцикліст прибув в пункт Б, другому до Б залишилося проїхати ще 9 км. Не затримуючись в пункті Б, перший відправився в зворотній шлях та через 5хв зустрів другого мотоцикліста. Знайти швидкість мотоциклістів та відстань між пунктами.

про публікацію авторської розробки
Додати розробку
