Підгототовка до ЗНО та НМТ (алгебра)

Підготовка до ЗНО та НМТ (алгебра)

 

 

     1.  Спростіть вираз:  . 

 

А	Б	В	Г	Д
				2

 

 Відповідь: Д

Розв’язання.    

 

  

 

2.   Знайдіть суму коренів рівняння: .

А	Б	В	Г	Д
20	8	6	64	16

 

 Відповідь: В

Розв’язання.

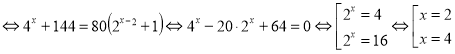 . Отже, сума коренів

      рівняння дорівнює: 2+4=6.

 

 

3.  За графіком функції    (див. малюнок 1) розв’яжіть нерівність .

 

А	Б	В	Г	Д

 

 Відповідь: Г

Розв’язання. Функція набуває не додатних значень (див. малюнок 1)  для . 

 

4.  Знайдіть кількість цілих значень аргументу області визначення  функції .

 

А	Б	В	Г	Д
5	4	10	6	7

 

   Відповідь: Б

Розв’язання. Маємо:  , тоді 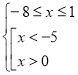, отже,  . ,  , чотири цілих значення.

 

5.    У  футбольних змаганнях беруть участь 15 команд. Турнір проходить у два кола (кожна з

      команд двічі зустрічається з будь-якою з інших команд). Скільки зустрічей буде проведе-

      но у цьому турнірі?

 

А	Б	В	Г	Д
225	196	210	105	98

 

       Відповідь: В

Розв’язання. Якщо в турнірі беруть участь  п  команд, тоді кількість матчів одного  кола дорівнює  ;  шукана кількість – вдвічі більша, отже, для маємо:  .

 

   6.  Скільки існує способів п’ятьом абітурієнтам обрати один із трьох факультетів універ- 

    ситету для подальшого навчання?

 

А	Б	В	Г	Д
243	15	125	120	8

 

     Відповідь: А

  Розв’язання. Перший абітурієнт обирає собі факультет у 3 способи. Другий – теж будь-який   з трьох факультетів. Так само - третій, четвертий і п’ятий абітурієнти. Отже, загальна кіль-кість способів:  .

 

 

      7.   Відомо, що: , .

 1) Знайдіть значення виразу:  .

 Відповідь: 154

 Розв’язання. Якщо , тоді , отже ;

  і 

 

2)  Обчисліть: .

Відповідь: 366

Розв’язання. Маємо:    

 

 

8.  Відстань від Києва до Харкова експрес може подолати за 5 годин. На скільки відсотків

      треба підвищити швидкість руху експресу, щоби цю відстань він подолав за 4 години?

     

      Відповідь: 25%

 Розв’язання. Нехай відстань між містами S км, тоді звичайна швидкість км/год,       підвищена - км/год, відсоткове відношення %, отже підвищити швидкість треба на 125 – 100 = 25%.

 

 

 

9. Послідовність задано формулою .  
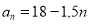   1.    Чи є серед елементів цієї  послідовності число  −30? Якщо є, то визначте його номер.

Якщо ні – запишіть у бланк число 1000.

 

Відповідь: так, номер 32.

Розв’язання. Розв’яжемо рівняння: ; число −30 є елемен-том цієї  послідовності з номером 32.

 

 

2.    Скільки невід’ємних елементів має ця послідовність?

 

Відповідь: 12

Розв’язання. Розв’яжемо нерівність ; отже, маємо 12 невід’ємних елементів.