Підготовка до НМТ з математики. Тест 1

Підготовка до НМТ з математики 2024.

  Тест із математики містить  22 завдання різних форм:з вибором однієї правильної відповіді з п’яти варіантів (15 завдань), на встановлення відповідності (3 завдання), відкритої форми з короткою відповіддю (4 завдання). Схема оцінювання: по 1 тестовому балу за кожну правильну відповідь на завдання з вибором однієї правильної відповіді, по 1 тестовому балу  – за кожну правильно визначену логічну пару в завданнях на встановлення відповідності та по 2 тестових бали  – за кожну правильну коротку відповідь. Максимальна кількість балів, яку можна набрати, правильно виконавши всі завдання, – 32.   

                                                Тест № 1

1.Яке одноцифрове число додати до 235, щоб утворене число було кратне 9?

А. 2  Б. 4  В. 6  Г. 7  Д. 8 

2.       Футболка коштує 450 грн. Яка буде ціна футболки після знижки на 18%?

      А. 81 грн  Б. 320 грн   В. 369 грн    Г. 280 грн   Д. 381 грн

3.       Якому з вказаних проміжків належить корінь рівняння 0,5^{х - 3} = 4^{х + 2} ?

      А. (-1; 0)    Б. (0; 1)   В. (1; 2)   Г. (-3; -1)   Д. (2; 3)

4. 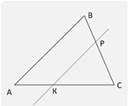      Пряма КР, яка перетинає сторони трикутника АВС (рис.), паралельна стороні АВ. Знайдіть довжину КР, якщо АВ = 8 см, ВР = 2 см, РС = 4 см.

        А. 6⅔ см  Б. 5⅓ см  В. 4⅙ см  Г. 5¼ см    Д. 3⅛ см

5.       Розв'яжіть систему рівнянь. У відповідь запишіть суму х + у, де (х; у) - розв'язок

3𝑥 + 5𝑦 = 2,

системи рівнянь {                          

3𝑥 − 𝑦 = −4.

        А.  -2   Б. -1  В. 1   Г. 0    Д. 2

6.       З міста А до міста В існує 5 туристичних маршрутів, а з міста В до міста С - 6 туристичних маршрутів. Скількома способами можна скласти туристичний маршрут з міста А через місто В до міста С?

      А. 720   Б.  10   В.  11   Г. 24   Д. 30

7.       Обчисліть 𝑑𝑥, якщо .

     А.  -4  Б. -2  В. -1   Г. 2  Д. 3

8. 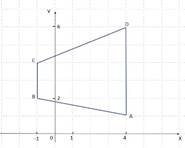      Знайдіть         площу         трапеції      ABCD, зображеної на рисунку.

А. 12  Б. 14,5   В. 16   Г. 17,5   Д. 18

9.       Функція F(x) = 4x² - 3 є первісною для f(x). Яка з даних функцій є первісною для f(x)?

      А. G(x) = 8x     Б. G(x) = 4x² + 2      В. G(x) = 4x² - 3x  

        Г. G(x) =  ^4𝑥3 − 3𝑥        Д. G(x) = 8x - 3

3

10.   Яке найменше ціле число є розв'язком нерівності

                                               ²   2

          0,6^𝑥−1 < (1 ) ?

3

      А. 2  Б. -2  В. -1  Г. 0  Д. 1

11.   Знайдіть більшу діагональ паралелограма, сторони якого дорівнюють 4 і 6, а   гострий кут 60⁰.

       А. √108   Б. √82  В. √76   Г. √48  Д. √28

12.   Сторона ВС трикутника АВС дорівнює 10 см, а кут А - 45⁰. Знайдіть радіус кола, описаного навколо трикутника АВС

          А. 8 см  Б. 6 см   В. 10√2 см  Г. 5√2 см  Д. 5 см

13.   Розв’яжіть рівняння |3x - 1| = 5. Знайдіть добуток його коренів.

     А. -2/3   Б. 4/5   В. -6/5  Г. -8/3   Д. 5/3

14.   На діаграмі відображено кількість проданих пар взуття в магазині за п’ять робочих днів. Яке з тверджень хибне?

А. У понеділок і середу продали на 23 пари більше, ніж у вівторок

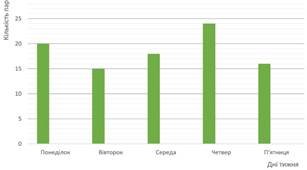Б. У вівторок продали найменше пар взуття

В. У п’ятницю і четвер продали у 2 рази більше, ніж в понеділок

Г. У четвер продали на 50% більше чим в п’ятницю

Д. У понеділок і середу продали більше пар взуття, чим у вівторок і четвер

15.   Діагональ грані куба дорівнює 4√2. Знайдіть площу поверхні куба.

А. 72   Б. 96   В.  64   Г. 112  Д. 144

16.   Установіть відповідність між рівняннями (1-3) та їх коренями (А-Д),         якщо а = 3.

1.   2log₃a = log₃x                                              A. 2,25

2.   log₃a - log₃2 = log₉x                                     Б. 4,5   

3.   log₃a + log₉4 = log₃x                                     В. 9   

                                                                        Г. 3 

                                                                        Д. 6 

17. Установіть відповідність між функцією (1-3) та її властивістю (А-Д)

1.у = 1/х                              А. Проходить через точку (2; 1) 

2.   у = log₃(x - 1)                  Б. Спадає при х є R

3.   y = 0,3^x                           В. Парна

                                           Г.  Область визначення – множина всіх чисел, більших                                                    від 1

                                          Д.   Спадає при всіх х є (-∞; 0), (0; +∞)

18.   Установіть відповідність між питанням (1-4) та правильною відповіддю на нього (А-Д).

1.Сторона ромба, площа якого 18√3, а гострий кут 60⁰.               А.9    

2.Діагональ прямокутника, площа якого 16, а кут між

    діагоналями 30⁰                                                                            Б.7     

3.Висота трапеції, основи якої 14 і 16, а площа 135.                   В. 5 

                                                                                                         Г. 8 

                                                                                                         Д.6              

19.   Точка рухається за законом х(t) = 3t² - 2t + 1 (м). У який момент часу   (t вимірюється   у с) її швидкість дорівнює 16 ^м/_с?

   Відповідь: 

20.   Розв'яжіть рівняння log₄(x - 4) + log₄(x + 8) = 3. Якщо корінь один, то запишіть його, якщо їх більше, то запишіть їх суму.

   Відповідь:

21.   Знайдіть об'єм конуса, якщо його твірна утворює з площиною основи кут 60⁰,        а радіус основи дорівнює 6. У відповідь подайте V⋅√3 : π.

    Відповідь: 

22.   При якому найбільшому цілому значенні параметра а корінь рівняння 

         8х + а = ^{3𝑎𝑥 − 2}  буде від'ємним?

2     Відповідь: 

Ключ до тесту

19.   3

20.   8

21.   216

22.   5