Підготовка до НМТ з математики. Тест 3

Підготовка до НМТ з математики 2024.

  Тест із математики містить  22 завдання різних форм:з вибором однієї правильної відповіді з п’яти варіантів (15 завдань), на встановлення відповідності (3 завдання), відкритої форми з короткою відповіддю (4 завдання). Схема оцінювання: по 1 тестовому балу за кожну правильну відповідь на завдання з вибором однієї правильної відповіді, по 1 тестовому балу  – за кожну правильно визначену логічну пару в завданнях на встановлення відповідності та по 2 тестових бали  – за кожну правильну коротку відповідь. Максимальна кількість балів, яку можна набрати, правильно виконавши всі завдання, – 32.   

                                                Тест № 3

1.Розв’яжіть рівняння ¹² = ^𝑥.

                                                             𝑥          3

А. -6 Б. 6  В. -2  Г. -6; 6  Д. 2 

2. 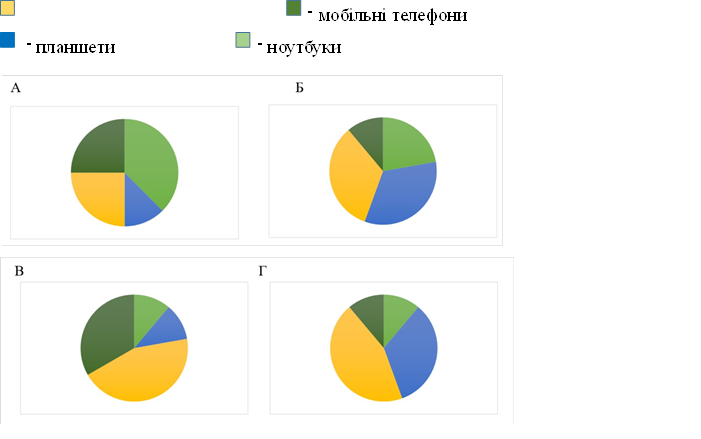  Інтернет магазин пропонує товари в такій кількості: 100 ноутбуків, 300 планшетів,  400 смартфонів, 100 мобільних телефонів. Яка з кругових діаграм найточніше відображає наявну кількість товару в магазині?

  - смартфони                                  

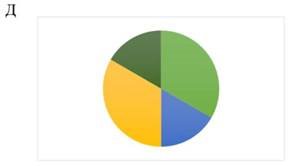
3.   Спростити вираз ¹         − ₂¹⁰

                                                     𝑥−5         𝑥 −25

      А. ¹    Б. ³   В. ¹   Г.  ⁻²  Д. ⁻¹ 

                 𝑥−5             𝑥+5            𝑥+5              𝑥−5           𝑥+5

4. 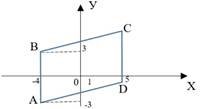  Знайдіть площу паралелограма ABCD (AB  OУ),

зображеного на рисунку.

       А. 18   Б. 24    В. 27    Г. 36    Д. 54

5.   Ціна товару зросла із 108 грн до 129,6 грн. На скільки відсотків збільшилася ціна товару?

А.  8 %  Б. 15 %  В. 18%  Г. 20 %  Д. 25 %

6.   Знайдіть бічну сторону рівнобедреного трикутника, якщо його площа дорівнює 12 см², а основа дорівнює 8 см.

А. 5 см  Б. 4 см  В. 3 см  Г. 2 см  Д. 1 см

7.   Який з виразів відповідає добутку 2𝑡𝑔𝛼 ∙ 𝑐𝑜𝑠²𝛼?

A. 2sin   Б. sin2   B. cos2   Г. 2cos  Д. sin

8.       При паралельному перенесенні графіка функції 𝑦  на 2 одиниці ліворуч       вздовж осі ОХ отримаємо графік функції:

А. 𝑦     Б. 𝑦    В. 𝑦      Г. 𝑦     Д. 𝑦  

9.       Розв'яжіть систему рівнянь. У відповідь запишіть суму х  у, де (х; у) - розв'язок

𝑥² − 3𝑥𝑦 = 6,

системи рівнянь {                           

𝑥 − 3𝑦 = 2.

        А.  9   Б. -1  В. 3   Г. -2    Д. 1

10.   Знайдіть довжину вектора 𝑎⃗ − ⃗𝑏⃗⃗⃗,  якщо 𝑎⃗(−1; 2; 1), 𝑏(1; 0; 2).

 A. √5      Б. 3   В. √2    Г. 2   Д. √6

11.   Розв’яжіть рівняння 𝑙𝑜𝑔.

    А. -4   Б. 1   В. 4  Г. 1; 4   Д. 5

12.   Яке з тверджень є істинним?

     А. Через будь-які дві прямі проходить площина і до того ж тільки одна

     Б. Мимобіжні прямі лежать в одній площині

     В. Якщо пряма паралельна площині, то вона паралельна до будь-якої прямої             цієї площини

     Г. Якщо пряма перпендикулярна до площини, то вона перпендикулярна до               будь-якої прямої цієї площини

     Д. Якщо дві вершини трикутника належать площині, то трикутник лежить в 

           даній площині 13. Знайдіть первісну для функції 𝑦 = ⁵₂ − 𝑥².

𝑥

     A. 𝑦 = ¹⁵₃ − ^𝑥3    Б. 𝑦 = − ⁵ − 2𝑥  B. 𝑦 = ¹⁰− 2𝑥  

                           𝑥            3                                2𝑥                                      𝑥

     Г. 𝑦 = ⁵₂ − ^𝑥3         Д. 𝑦 = − ⁵ − ^𝑥3

                          𝑥            3                                        𝑥         3

14.             Двоє друзів розв’язують олімпіадну задачу з математики. Ймовірність того, що розв’яже перший дорівнює 0,8, другий – 0,9. Яка ймовірність того, що один з них розв’яже задачу?

А. 0,17   Б. 0,26  В. 0,02  Г. 0,98  Д. 0,72

15.             Знайдіть бічну поверхню конуса, якщо довжина його основи 10π см, а висота дорівнює 12 см. 

А. 65π см Б. 60π см  В. 48π см  Г. 36π см  Д. 24 π см

16.             До кожного початку речення (1–3) доберіть його закінчення (А – Д) так, щоб    утворилося правильне твердження.

1.   Якщо  4^𝑥 ∙ 16 = 4^𝑦,  то                                                    A. у = х + 4

2.   Якщо     16⁻¹ ∙ 2^𝑦 = 2^𝑥,  то                                             Б. у = 4 – х     

3.   Якщо       _𝑦                ^𝑥,        то                                               В. у = х + 2 

16

                                                                                                Г. 𝑦 = ^𝑥−4

2

                                                                                               Д. 𝑦 = ^2−𝑥

4

17. Установіть відповідність між функцією (1-3) та її властивістю (А-Д)

1.                                     А. Графік функції проходить через точку (1; 0) 

2.   у = 3𝑥 − 1                              Б. Функція спадає при x < 0,5

3.   y = 𝑙𝑜𝑔_0,5(2𝑥 − 1)                  В. Найменше значення функції 0

                                                     Г. Функція зростає при х  R                                              

                                                    Д.   Функція періодична

18. З точки Р до площини проведено перпендикуляр РО і похилу РВ. Довжина перпендикуляра дорівнює 6 см, а довжина проєкції похилої дорівнює 8 см. Установіть відповідність між запитанням (1-3) та правильною відповіддю до нього (А-Д).

1.   Довжина похилої                                                                               А. 4 см

2.   Відстань від середини перпендикуляра до середини похилої      Б. 6,4 см

3.   Проєкція перпендикуляра на похилу                                              В. 10 см

                                                                                                                 Г. 2 см                                                                                                                  Д. 3,6 см      

19.   Обчисліть:  

   Відповідь: 

20.   Скільки трицифрових чисел, кратних 5, можна скласти з цифр 0; 3; 5; 7; 9, якщо цифри не повторюються.

   Відповідь:

21.   Основою прямої чотирикутної призми є ромб зі стороною 4 і гострим кутом        60⁰. Знайдіть площу більшого діагонального перерізу призми, якщо висота       призми 3. 

    Відповідь: 

22.   Знайдіть суму всіх цілих значень параметра а, при яких рівняння        5^х  8 – 4а = 5^х  а – 6 має розв’язок?     

    Відповідь: 

Ключ до тесту

19.   6

20.   21

21.   36

22.   27