Підготовка до НМТ з математики. Тест 2
Підготовка до НМТ з математики 2024.
Тест із математики містить 22 завдання різних форм:з вибором однієї правильної відповіді з п’яти варіантів (15 завдань), на встановлення відповідності (3 завдання), відкритої форми з короткою відповіддю (4 завдання). Схема оцінювання: по 1 тестовому балу за кожну правильну відповідь на завдання з вибором однієї правильної відповіді, по 1 тестовому балу – за кожну правильно визначену логічну пару в завданнях на встановлення відповідності та по 2 тестових бали – за кожну правильну коротку відповідь. Максимальна кількість балів, яку можна набрати, правильно виконавши всі завдання, – 32.
Тест № 2
1.Знайдіть суму коренів рівняння 5 = 𝑥.
𝑥−3 2
А. 3 Б. -2 В. -3 Г. 10 Д. 2
2. Яка з функцій парна?
А. у = х3 + 1 Б. у = 3х В. у = х4 + cosx
Г. y = sinx - 2 Д. y = x2 + 2x
3. Cкільки цілих розв’язків має нерівність -9 ≤ 5x – 1 < 4?
А. 5 Б. 4 В. 3 Г. 2 Д. 1
4. У арифметичній прогресії (ап) п-й член прогресії заданий формулою ап = 5п – 3. Знайдіть різницю арифметичної прогресії.
А. 4 Б. 5 В. -3 Г. -5 Д. 2
5. Розв'яжіть систему рівнянь. У відповідь запишіть суму х у, де (х; у) - розв'язок
5𝑥−3 = 1,
системи рівнянь {𝑥2 + 4𝑦 = 1.
А. 1,5 Б. -1 В. 5 Г. 1 Д. -6
6. Яка з точок належить площині (YOZ)?
А. (-2; 0; 1) Б. (3; -2; 1) В. (0; 5; -2)
Г. (1; -1; 0) Д. (0; 0; 4)
7. Скільки коренів рівняння √2𝑐𝑜𝑠𝑥 = 1 належать проміжку (0; 2π)?
А. 0 Б. 1 В. 2 Г. 3 Д. 4
8. Знайдіть об’єм циліндра, висота якого дорівнює діаметру d основи циліндра.
А. 𝜋𝑑3 Б. 𝜋𝑑3 В.𝜋𝑑3 Г. 𝜋𝑑3 Д. 𝜋𝑑3
3 4 6 2 9
9. Знайдіть медіану ряду даних вибірки 7; 4; 5; 7; 4; 6; 10; 9.
А. 5,5 Б. 5 В. 6 Г. 6,5 Д. 7 10. Обчисліть 𝑦 , якщо 𝑦
−3𝑥 = 5.
𝑥 𝑥
А. -4 Б. -2 В. 2 Г. 6 Д. 8
11. 
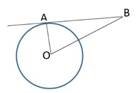З точки В, до кола з центром в точці О, проведена дотична
ВА (рис.). Знайдіть кут АОВ, якщо АО дорівнює 5 см, ОВ = 10 см.
А. 600 Б. 450 В. 300 Г. 900 Д. 1200
12. Розв’яжіть нерівність log0,5(2 – x) > -1.
А. (0; +∞) Б. (0; 2) В. (-∞; 2) Г. (2; +∞) Д. (0; 1)
13. Яке з тверджень є правильним?
А. Сума кутів при будь-якій стороні трапеції дорівнює 1800.
Б. Діагоналі ромба рівні.
В. Сума протилежних сторін вписаного чотирикутника рівна.
Г. У будь-який ромб можна вписати коло.
Д. Радіус кола, описаного навколо прямокутника – це четверта частина його діагоналі.
14. Спростіть вираз 𝑥42−+𝑥22𝑥.
A. 𝑥2 Б. 4𝑥−2𝑥 B. 2−𝑥𝑥 Г. 𝑥𝑥−22 Д. 𝑥−𝑥2
15. При якому значенні у вектори 𝑎⃗ (2; 𝑦) і 𝑏⃗⃗ (−3; 6) колінеарні? А. -4 Б. -2 В. -1 Г. 2 Д. 3
16. Установіть відповідність між виразами (1-3) та проміжками, яким належать їх значення (А-Д).
A. (2; 4)
2. 3-2 81 Б. (5; 7)
3. sin4π + cos3π В. (-4; -2)
Г. (-2; 0)
Д. (8; 10)
17. Установіть відповідність між функцією (1-3) та її властивістю (А-Д)
1.у = 𝑥2 + 2𝑥 + 3 А. Графік функції симетричний відносно осі ОУ
2. у = 3𝑥−1 Б. Функція спадає при x < 1
3. y = 𝑙𝑜𝑔6(𝑥 − 1) В. Найменше значення функції 2
Г. Графік функції перетинає пряму у = 9 в точці з абсцисою х = 3.
Д. Область визначення функції х є (1; +∞)
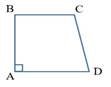18. Дано прямокутну трапецію ABCD, в яку можна вписати коло (рис.). Більша бічна сторона трапеції 25 см, основи трапеції дорівнюють 21 см і 28 см.
Установіть відповідність між питанням (1-3) та правильною відповіддю на нього (А-Д).
1. Радіус кола, вписаного в дану трапецію А. 24 см
2. Висота трапеції Б.7 см
3. Середня лінія трапеції В. 12,5 см
Г. 12 см
Д. 24,5 см
19. Знайдіть значення похідної функції у = х3 – 2х + ln(2x) в точці з абсцисою х = 1.
Відповідь:
20. У кафе «Мрія» є тістечка 5 видів та 6 різних видів соку. Марійка вирішила замовити собі 2 різних тістечка та 1 сок. Скількома способами Марійка може зробити замовлення?
Відповідь:
21. У правильній чотирикутній піраміді бічне ребро дорівнює 6√2 см та утворює з площиною основи кут 450. Знайдіть об’єм піраміди.
Відповідь:
22. При якому найменшому цілому додатному значенні параметра а обидва корені рівняння х2 – (2а – 1)х + а2 – а – 6 = 0 будуть додатними?
Відповідь:
Ключ до тесту
|
|
|
|
|
|
|
|
|
19. 2
20. 60
21. 144
22. 4
-
Дякую.
про публікацію авторської розробки
Додати розробку