Підготовка до НМТ з математики. Тест 4

Підготовка до НМТ з математики 2024.

  Тест із математики містить  22 завдання різних форм:з вибором однієї правильної відповіді з п’яти варіантів (15 завдань), на встановлення відповідності (3 завдання), відкритої форми з короткою відповіддю (4 завдання). Схема оцінювання: по 1 тестовому балу за кожну правильну відповідь на завдання з вибором однієї правильної відповіді, по 1 тестовому балу  – за кожну правильно визначену логічну пару в завданнях на встановлення відповідності та по 2 тестових бали  – за кожну правильну коротку відповідь. Максимальна кількість балів, яку можна набрати, правильно виконавши всі завдання, – 32.   

                                                Тест № 4

1.    Знайдіть добуток коренів рівняння 2𝑥² + 5𝑥 − 4 = 0.

А. -5 Б. 2   В. -2,5  Г. -4  Д. -2 

2.    Яка найменша кількість метрів тканини має бути в сувої, щоб її можна було розрізати на куски по 4 м, або по 6 м?

  А. 6 м  Б. 10 м  В. 12 м   Г. 18 м  Д. 24 м                  

3.    Якщо  ^𝑎            = 4, то с = 

𝑏+𝑐

      А. 𝑏 − 4𝑎    Б. ^𝑎−𝑏   В. ^𝑎−4𝑏   Г.  ^4𝑎−𝑏  Д. 4𝑎 − 𝑏 

                                                   4                    4                      4

4.    Точка С належить відрізку АВ. Довжина відрізка АС у 5 разів більша від

довжини відрізка ВС. Якому з чисел може дорівнювати довжина відрізка АВ?

       А. 16   Б. 22   В. 28    Г. 36    Д. 44

5.    Знайдіть найбільше ціле число, що є розв’язком нерівності  

      0,4^x-1 ≥ 2,5.

А.  -1   Б. 0  В. 1  Г. -2  Д. 2

6.    У прямокутному рівнобедреному трикутнику гіпотенуза дорівнює 6. Знайдіть площу трикутника.

А. 9   Б. 12  В. 18  Г. 24  Д. 36

7.    Розв'яжіть систему рівнянь. У відповідь запишіть суму х + у, де (х; у) - розв'язок log₄(𝑥 − 3) = 1,

системи рівнянь {log(6𝑥 − 3𝑦) = −2.

A.  4     Б. 11     B.  12     Г.  18     Д. 24

8.   Яка з точок лежить на колі х² + у² = 12?

А. (2; -3)  Б. (0; 4)  В.  

9.   У трикутнику АВС АС = 6, В = 30⁰, С = 45⁰. Знайдіть сторону АВ.

        А.      Д.  

10.             Розв’яжіть рівняння  2cos2x = 1. Знайдіть найменший додатній кут (в        градусах). 

 A. 15⁰      Б. 30⁰   В. 45⁰    Г. 60⁰   Д. 75⁰   

11.   Обчисліть .

    А. 1/2   Б. 1/4   В. 1/8   Г. 1/16   Д. 2

12. 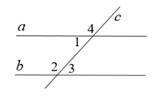  На рисунку зображені дві паралельні прямі a i b та січна

с. Які з тверджень є істинними?

1.   1 + 3 = 180⁰

2.   4 = 3 

3.   4 + 3 = 180⁰

4.   1 = 2

5.   4 = 2

А. 1, 3   Б. 3, 4, 5   В. 2, 5  Г. 2, 4  Д. 3,5

13.   Знайдіть кутовий коефіцієнт дотичної, проведеної до графіка функції         𝑦 =     ⁴ в точці з абсцисою х = 2.

𝑥−1

     A. -6     Б.  -2    B.  -4      Г.  2       Д. 4

14.   Знайдіть суму чотирьох послідовних членів прогресії, у якій перший член прогресії 1/3, а четвертий дорівнює 9.  А. 25/6   Б. 31/3  В. 28/3  Г. 40/3  Д. 37/6

15.   Знайдіть об’єм кулі, якщо площа її поверхні 144π см². 

А. 216π см³ Б. 288π см³  В. 196π см³  Г. 144π см³  Д. 72 π см³

16.   Кожному з виразів (1–3) поставте у відповідність його значення (А – Д), якщо      х = 3.

1. ¹        +      ¹                                                                       A. 3,5

       𝑥−4        8−2𝑥

2 (𝑥² − 16): (2𝑥 − 8)                                                          Б. -2,5 3.   1 − ^𝑥−3                                                                            В. -0,5 𝑥+4

                                                                                                Г. 1

                                                                                               Д. 2

17. Установіть відповідність між функцією (1-3) та її властивістю (А-Д)

1.   у = 2𝑠𝑖𝑛𝑥                                  А. Графік функції проходить через точку (0; 2) 

2.   у = с𝑜𝑠2𝑥                               Б. Період функції Т = π/2

3.   y = 2𝑡𝑔𝑥                                  В. Функція спадає при всіх х  R

                                                     Г. Графік функції з прямою у = 2 має безліч                                                            спільних точок                                               

                                                    Д.   Функція парна

18.             Дано точку Р(-4; 0; 1). Продовжіть речення (1-3) так, щоб воно стало правильним (А-Д).

1.Точка, симетрична точці Р відносно (0; 0; 0)                   А. (-4; 0; -1)

2.Точка, симетрична точці Р відносно точки (1; -2; -1)     Б. (4; 0; 1)

3.Точка, симетрична точці Р відносно осі аплікат              В. (4; 0; -1)

                                                                                                 Г. (6; -4; -3)

                                                                                                  Д. (-2; -3; 3)

19.             Знайдіть площу S фігури, обмежену лініями у = х² і у = х³. У відповідь запишіть S  3.

   Відповідь: 

20.             У відділі «Канцтовари» знижка на ручки і олівці. Ймовірність придбати по знижці одну ручку дорівнює 4/11. Знайдіть відношення кількості олівців до ручок, які продаються за знижкою.

   Відповідь:

21.             У правильній трикутній піраміді бічне ребро дорівнює 10, а висота піраміди дорівнює 6. Знайдіть площу перерізу піраміди, що проходить через одне з бічних ребер піраміди та її висоту.

    Відповідь: 

22.             При якому цілому значенні параметра а один з коренів рівняння        х² – (а + 7)х + 3а + 12 = 0 належить проміжку (2; 4), а другий (-5; -3)?     

    Якщо таких значень не одне, то у відповідь запишіть їх суму.

    Відповідь: 

Ключ до тесту

19.   0,25

20.   1,75

21.   36

22.   -8